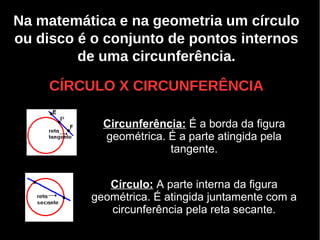
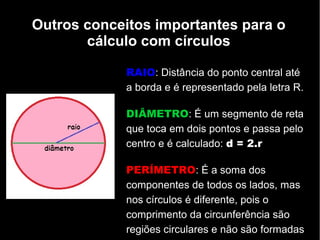
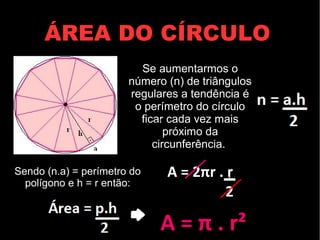
O documento discute os componentes e conceitos fundamentais do círculo, incluindo circunferência, raio, diâmetro, perímetro e área. Exemplos mostram como calcular o perímetro percorrido em voltas em torno de um círculo e a área de regiões circulares.

1. ÁREA EÁREA E
COMPONENTES DOCOMPONENTES DO
CÍRCULO
Autor:
Rodrigo Lopes Pinto
jupteraple@bol.com.br

2. O círculo começou a ser estudado a
aproximadamente 4 mil anos atrás e está
presente no nosso cotidiano.
Exemplos: Moedas, discos, rodas, etc.

3. O compasso é o instrumento
ideal para fazer uma
circunferência ou círculo.

4. Na matemática e na geometria um círculo
ou disco é o conjunto de pontos internos
de uma circunferência.
CÍRCULO X CIRCUNFERÊNCIACÍRCULO X CIRCUNFERÊNCIA
Circunferência: É a borda da figura
geométrica. É a parte atingida pela
tangente.
Círculo: A parte interna da figura
geométrica. É atingida juntamente com a
circunferência pela reta secante.

5. Outros conceitos importantes para o
cálculo com círculos
RAIO: Distância do ponto central até
a borda e é representado pela letra R.
DIÂMETRO: É um segmento de reta
que toca em dois pontos e passa pelo
centro e é calculado: d = 2.r
PERÍMETRO: É a soma dos
componentes de todos os lados, mas
nos círculos é diferente, pois o
comprimento da circunferência são
regiões circulares e não são formadas

6. Exemplo: Determine quantos metros, aproximadamente,
um homem percorrerá se correr oito voltas completas em
torno de um canteiros circular com raio de dois metros?
C = 2π.r
C = 3,14 x 2
C = 12,56
C = perímetro
π = 3,14
R = 2
Como são 8 voltas, então:
12,56 x 8 = 100,48
R: O homem percorrerá aproximadamente 100 metros.

11. Se aumentarmos o
número (n) de triângulos
regulares a tendência é
o perímetro do círculo
ficar cada vez mais
próximo da
circunferência.
n=
a.h
2
n=
a.h
2
Sendo (n.a) = perímetro do
polígono e h = r então:
A = 2πr . r
2
'
A = π . r²
ÁREA DO CÍRCULOÁREA DO CÍRCULO

12. Exemplo 1: Determine quantos m² de grama serão
necessários para preencher uma praça circular com raio
de 20 metros?
A = π . r²
A = 3,14 x 20²
A = 3,14 x 400
A = 1.256
A = área
π = 3,14
r = 20
R: Serão necessários 1.256 m² de grama para prencher a
praça.

13. Exemplo 2: Determine a área da região em destaque
representada pela figura onde região maior tem raio igual
a 10 metros e a região menor tem raio igual a 3 metros?
A = π . r²
A = 3,14 x 10²
A = 3,14 x 100
A = 314
A = π . r²
A = 3,14 x 3²
A = 3,14 x 9
A = 28,26
Como o exercício pede a área em destaque então:
314 – 28,26 = 285,74
R: A área da figura em destaque é de 285,74 m².