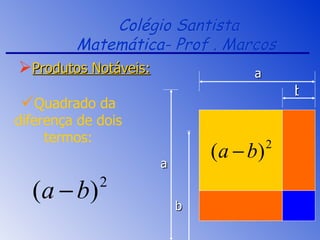
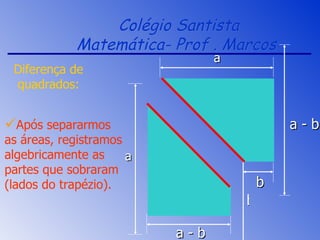
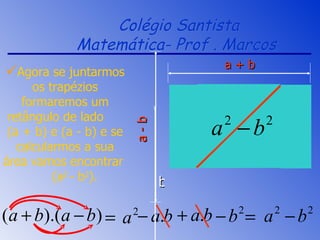
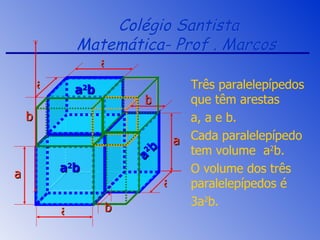
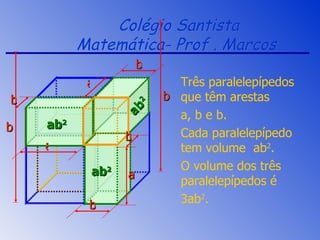
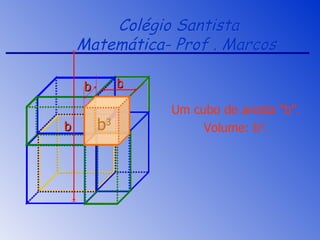
1) O documento discute produtos notáveis e fatoração. 2) São explicados o quadrado da soma e diferença de termos, a diferença e cubo de quadrados e a aplicação da propriedade distributiva. 3) Exemplos demonstram como decompor volumes de figuras geométricas usando produtos notáveis e fatoração.

1. Colégio Santista Matemática- Prof . Marcos Fatoração 7ª Série Unidade Temática: Produtos Notáveis

2. Colégio Santista Matemática- Prof . Marcos Produtos Notáveis: Quadrado da Soma de dois termos: Soma das Áreas= b a b a

3. Colégio Santista Matemática- Prof . Marcos Produtos Notáveis: Quadrado da diferença de dois termos: b a b a

4. Colégio Santista Matemática- Prof . Marcos Produtos Notáveis: Quadrado da diferença de dois termos. Calculando a área que sobrou teremos: a - b a - b

5. Colégio Santista Matemática- Prof . Marcos Produtos Notáveis: Diferença de quadrados: b a a b

6. Colégio Santista Matemática- Prof . Marcos Após a subtração da maior área pela menor área, marcamos com uma diagonal separando a área restante dividindo-a em duas partes, que são dois trapézios.

7. Colégio Santista Matemática- Prof . Marcos Após separarmos as áreas, registramos algebricamente as partes que sobraram (lados do trapézio). Diferença de quadrados: b a a b a - b a - b

8. Colégio Santista Matemática- Prof . Marcos Agora se juntarmos os trapézios formaremos um retângulo de lado (a + b) e (a - b) e se calcularmos a sua área vamos encontrar (a 2 - b 2 ). a + b a - b b

9. Colégio Santista Matemática- Prof . Marcos Considere um cubo de aresta “a + b”, como o da figura ao lado. O volume de um cubo de arestas ℓ é ℓ 3 , então o volume do cubo representado pela figura é (a+b) 3 . O Cubo da soma de dois termos: a b b a a b

10. Colégio Santista Matemática- Prof . Marcos Vamos separar as partes em que o cubo está dividido: Um cubo de aresta “a”. Volume: a 3 . a 3 a a a

11. Colégio Santista Matemática- Prof . Marcos Três paralelepípedos que têm arestas a, a e b. Cada paralelepípedo tem volume a 2 b. O volume dos três paralelepípedos é 3a 2 b. a 2 b a 2 b a 2 b b b a a a a b a a

12. Colégio Santista Matemática- Prof . Marcos Três paralelepípedos que têm arestas a, b e b. Cada paralelepípedo tem volume ab 2 . O volume dos três paralelepípedos é 3ab 2 . ab 2 ab 2 ab 2 b b a b a a b b b

13. Colégio Santista Matemática- Prof . Marcos Um cubo de aresta “b”. Volume: b 3 . b 3 b b b

14. Colégio Santista Matemática- Prof . Marcos Somando todos esses volumes temos: Como o volume do todo é igual à soma dos volumes das partes, temos: a 2 b a 2 b a 3 ab 2 a 2 b ab 2 ab 2 b 3

15. Colégio Santista Matemática- Prof . Marcos Esse mesmo resultado pode ser obtido através do seguinte cálculo: Aplicando a propriedade distributiva:

16. Colégio Santista Matemática- Prof . Marcos Portanto: 1º Termo 2º Termo Cubo do 1º Termo. Cubo 2º Termo. 3 x ( o quadrado do 1º termo) x (2 º termo). 3 x (1º termo) x ( o quadrado do 2 º termo).

17. Colégio Santista Matemática- Prof . Marcos Esse mesmo resultado pode ser obtido através do seguinte cálculo: Aplicando a propriedade distributiva: O Cubo da diferença de dois termos:

18. Colégio Santista Matemática- Prof . Marcos Portanto: 1º Termo 2º Termo Cubo do 1º Termo. Cubo 2º Termo. 3 x ( o quadrado do 1º termo) x (2 º termo). 3 x (1º termo) x ( o quadrado do 2 º termo).

19. Colégio Santista Matemática- Prof . Marcos Hora da revisão: Diferença de quadrados: Quadrado da soma de dois termos: Quadrado da diferença de dois termos: Cubo da soma de dois termos: Cubo da diferença de dois termos:

20. Colégio Santista Matemática- Prof . Marcos Fator Comum Fatoração: Calculando-se a Área: x a x

21. Colégio Santista Matemática- Prof . Marcos Fator Comum Fatoração: Colocando o fator em evidência teremos: Fazendo o fator comum entre as áreas encontraremos :2a 2a 4 a a

22. Colégio Santista Matemática- Prof . Marcos por agrupamento: am Fatoração: bm an bn b a m n

23. Colégio Santista Matemática- Prof . Marcos Fazendo o fator comum entre os termos apresentados, volta-se ao início. Aplicando o fator comum duplamente: