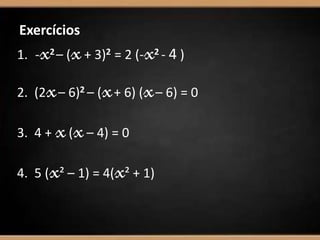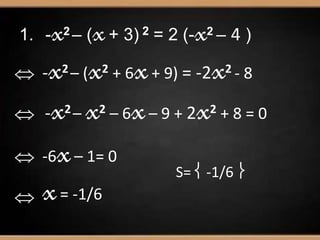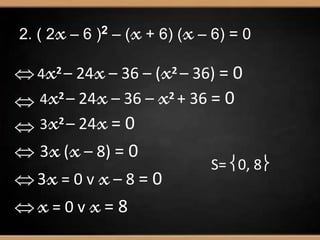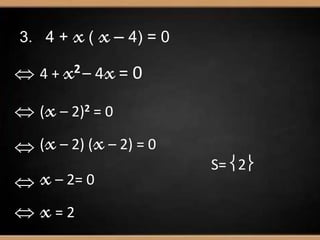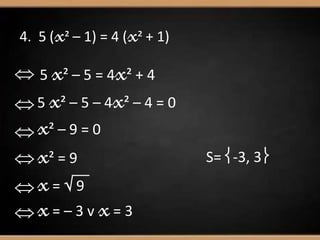O documento apresenta os métodos para resolver equações do 2o grau: quadrado de um binómio, diferença de quadrados, factorização e lei do anulamento do produto. Exemplos são fornecidos para ilustrar cada método, resultando em soluções como x=4, x=-4/4, ou equações impossíveis.

2. ax2 + bx+ c = 0
Uma equação do 2º grau é uma equação que, na
forma canónica, se escreve da seguinte forma:
com a, b & c  IR, a0

3. Para resolvermos equações do 2º grau, usamos:
• Quadrado de um binómio
• Diferença de quadrados
• Factorização
• Lei do Anulamento do Produto

4. Quadrado de um Binómio
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
ou

5. Diferença de Quadrados
(a + b) (a – b) = a2 – b2
porque
(a + b) (a – b) =
a2 – ab + ab – b2=
a2 – b2

6. –
–
Factorização
4x2 – 2x = 2x (2x– 1)
9x2 – 2x = x (9x– 2)

7. Lei do Anulamento do Produto
a x b = 0  a = 0 v b = 0
“v” lê-se “ou”
(x-5) (x+2) = 0 
x-5 = 0 v x+2 = 0 
x= 5 v x= -2

8. 1. x2 – 16 = 0 Diferença de Quadrados
(x+ 4) (x– 4) = 0 Lei do Anulamento do
Produto
 x+ 4 = 0 v x– 4 = 0
 x= -4 v x= 4
S= -4, 4

9. 2. x2 – 32x+ 16 = 0
 (x– 4)2
= 0
 (x– 4) (x– 4) = 0
 x – 4 = 0 v x– 4 = 0
 x= 4
Quadrado de um Binómio
Lei do Anulamento do
Produto
S= 4

10. 3. 27x2 –12x = 0
3x ( 9x– 4) = 0
 3x= 0 v 9x– 4 = 0
x= 0 v 9x= 4


x= 0 v x= 4/9
S= 4/9, 4
Factorização
Lei do Anulamento do
Produto

11. 4. 4x2 + 49 = 0
 4x2 = – 49
S= 
Equação impossível, porque a raiz quadrada
de um número nunca é negativa.
 4x= – 49

12. Exercícios
1. -x2– (x+ 3)2 = 2 (-x2 - 4 )
2. (2x– 6)2 – (x+ 6) (x– 6) = 0
3. 4 + x(x– 4) = 0
4. 5 (x² – 1) = 4(x² + 1)

13. 1. -x2 – (x+ 3) 2 = 2 (-x2 – 4 )
 -x2– (x2 + 6x+ 9) = -2x2 - 8
-x2– x2 – 6x– 9 + 2x2 + 8 = 0
 -6x– 1= 0
 x= -1/6
S=  -1/6 

14. 2. ( 2x– 6 )2 – (x+ 6) (x– 6) = 0
4x2 – 24x– 36 – (x2 – 36) = 0
 4x2 – 24x– 36 – x2 + 36 = 0
 3x2 – 24x= 0
 3x(x– 8) = 0
3x= 0 v x– 8 = 0
x= 0 v x= 8
S= 0, 8

15. 3. 4 + x( x– 4) = 0
 4 + x2 – 4x= 0
 (x– 2)2 = 0
 (x– 2) (x– 2) = 0
 x– 2= 0
 x= 2
S= 2

16. 4. 5 (x² – 1) = 4 (x² + 1)
 5 x² – 5 = 4x² + 4
5 x² – 5 – 4x² – 4 = 0
x² – 9 = 0
x² = 9
x=  9
x= – 3 v x= 3
S= -3, 3