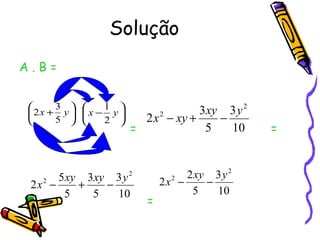
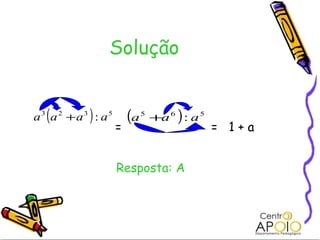
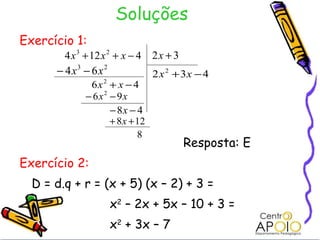
O documento discute polinômios, incluindo sua definição como uma soma de monômios, classificação por número de termos, determinação do grau, ordenação, soma, subtração, multiplicação e divisão. Os principais pontos cobertos são como identificar o grau de um polinômio, ordenar e completar polinômios, aplicar a propriedade distributiva para somar, subtrair e multiplicar polinômios, e realizar divisões de polinômios usando uma abordagem semelhante à divisão de números naturais.

1. Polinômios

2. O que é um polinômio Classificar os polinômios Determinar o grau de um polinômio Ordenar e completar um polinômio Somar e subtrair polinômios Multiplicar polinômios Dividir um polinômio por um monômio Dividir um polinômio por outro polinômio Ao final dessa aula você saberá...

3. O que é polinômio? É uma adição algébrica de monômios . Exemplos de polinômios 4a 3 x 2 +3y 4m 2 +3m+1 Atenção! O 1º exemplo é a soma do monômio 4a 3 com o zero.

4. Classificação dos polinômios Monômios  polinômios com apenas 1 termo Binômios  polinômios com 2 termos Trinômios  polinômios com 3 termos Não existe um nome específico para os polinômios que apresentam 4 ou mais termos.

5. Como sabemos o grau de um polinômio? Verificamos o grau de cada monômio da expressão. O maior deles é o grau do polinômio. Exemplos:  polinômio do 5º grau  polinômio do 4º grau

6. Observação Polinômios com uma só variável geralmente são apresentados ordenadamente, começando pelo monômio de maior grau. Exemplo: Ordenar o polinômio 2x 2 + x + 5x 3 + 9. Resposta: 5x 3 + 2x 2 + x + 9 Verifique que o 9 é um monômio de grau zero . 9 = 9x 0

7. O que são polinômios incompletos em relação a uma variável? Se um polinômio estiver ordenado e o coeficiente de algum termo for zero , então esse polinômio é incompleto . Exemplos: x 4 – 3 = x 4 + 0x 3 + 0x 2 + 0x – 3 8m 3 + m 2 = 8m 3 + m 2 + 0m + 0

8. Qual é a regra para somar e subtrair polinômios? Basta fazer a redução dos termos semelhantes . Exemplos: a) (y 3 – 2y 2 + 5) + (2y 3 – 5y – 7) = y 3 – 2y 2 + 5 + 2y 3 – 5y – 7 = 3y 3 – 2y 2 – 5y – 2 b) (6m 2 – 7mn + 8n 2 ) – (8mn + 5m 2 – 7n 2 ) = 6m 2 – 7mn + 8n 2 – 8mn – 5m 2 + 7n 2 = m 2 – 15mn + 15n 2

9. Tente fazer sozinho! Dados os polinômios: A = 5x 2 – 3x + 4 B = 2x 2 + 4x – 3 C = x 2 – 3x Calcule A + C – B

10. Solução A + C – B = (5x 2 – 3x + 4) + (x 2 – 3x) – (2x 2 + 4x – 3)= 5x 2 – 3x + 4 + x 2 – 3x – 2x 2 – 4x + 3 = 5x 2 + x 2 – 2x 2 – 3x – 3x – 4x + 4 + 3 = 4x 2 – 10x + 7

11. Como multiplicamos polinômios? Aplicando a propriedade distributiva . Exemplos: – y 2 (y 3 – 2y 2 + 1) = – y 5 + 2y 4 – y 2 (a + b) (a + b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2

12. Tente fazer sozinho! Seja A = e B = Calcule AB.

13. Solução A . B = = = =

14. Como dividimos um polinômio por um monômio? Aplicando a propriedade distributiva . Exemplos: (15m 3 – 10m 2 ) : (-5m) = - 3m 2 + 2m

15. Tente fazer sozinho! (Cesgranrio - RJ) Simplificando a expressão , encontramos: a) 1 + a b) a 2 + a c) 1 + 5a d) 1 – a e) a 3

16. Solução = = 1 + a Resposta: A

17. Para dividir um polinômio por outro também usamos a distributiva? Não! Nesse caso temos que armar a conta , como se fosse uma divisão de números naturais: e seguir os passos descritos nos próximos exemplos. quociente dividendo divisor resto

18. Exemplo 1 Calcule: : 1º passo: ordenar e completar o dividendo , se necessário. Nesse caso não será necessário 2º passo: armar a conta .

19. 3º passo: dividir o 1º termo do dividendo pelo 1º termo do divisor. 4º passo: multiplicar o resultado por cada termo do divisor, colocando a resposta embaixo do dividendo, com o sinal contrário . Para facilitar o próximo passo, procure colocar os termos semelhantes na mesma direção.

20. 5º passo: efetuar a soma da 1ª com a 2ª linha, obtendo um novo dividendo. 6º passo: Verificar se o 1º termo do novo dividendo é menor que o 1º termo do divisor. Caso não seja, voltamos ao 3º passo. 15 3   x 15 3   x

21. Logo, quociente = x – 3 e resto = 0. Importante! Note que para toda divisão vale dizer que dividendo = divisor x quociente + resto, ou seja, D = d.q + r 15 3   x 15 3   x

22. Exemplo 2 Encontre o resto da divisão de por . 1º passo: 2º passo: 3º passo:

23. 4º passo: 5º passo: 6º passo: como o 1º termo do novo dividendo é menor que o 1º termo do divisor , não podemos continuar a divisão. Logo, o quociente = x e o resto = - x +1

24. Tente fazer sozinho! 1) (Uespi) O resto da divisão do polinômio 4x 3 + 12x 2 + x – 4 por 2x + 3 é: a) 1 b) 2 c) 4 d) 6 e) 8 2) Determine o polinômio que dividido por x + 5, tem por quociente x – 2 e resto 3.

25. Soluções Exercício 1: Resposta: E Exercício 2: D = d.q + r = (x + 5) (x – 2) + 3 = x 2 – 2x + 5x – 10 + 3 = x 2 + 3x – 7