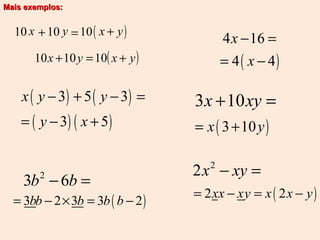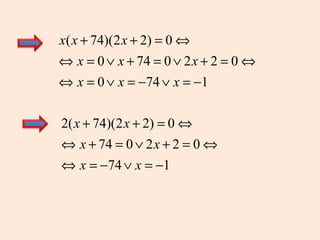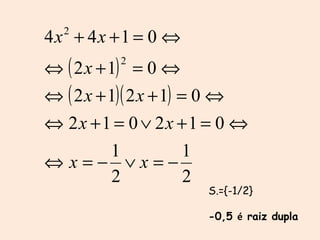O documento discute monômios e polinômios, incluindo:
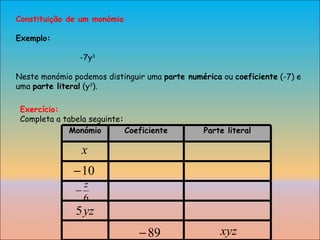
1) A definição de monômios e polinômios, com exemplos de cada um.
2) Como determinar o grau de um monômio ou polinômio.
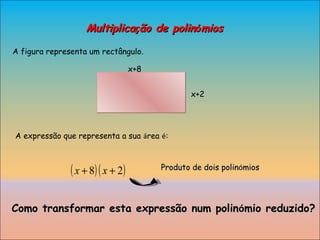
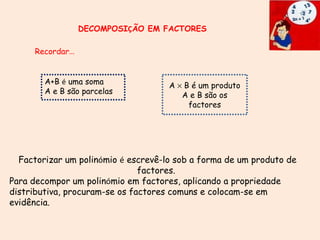
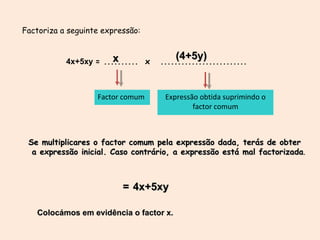
3) Operações com polinômios como adição, subtração, multiplicação e fatores comuns.