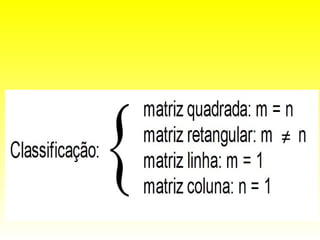
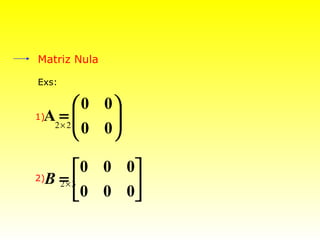
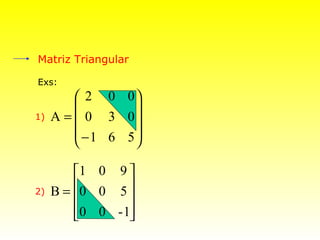
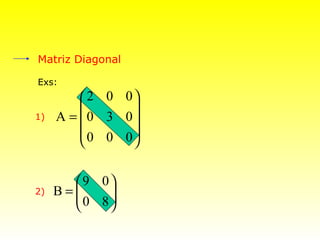
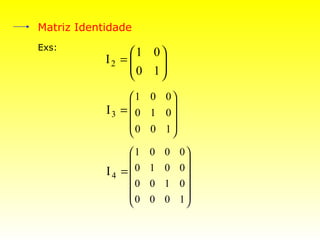
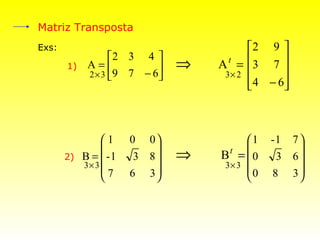
O documento descreve conceitos básicos sobre matrizes, incluindo: (1) matrizes são tabelas formadas por linhas e colunas; (2) exemplos de matrizes retangulares e quadradas; (3) elementos de uma matriz genérica; (4) tipos especiais de matrizes como linha, coluna, nula, triangular, diagonal, identidade, transposta, simétrica.

2. Conceito: São tabelas formada por linhas e
colunas

3. Na prática...
 3 0
  3 linhas
1) A = − 1 7 
 8 5
 
2 colunas
⇒Matriz 3x2
(matriz retangular)

4. 1 4 − 9 
 
2) B =  4 6 3 3 linhas
 0 0 2 / 3
 
3 colunas
⇒Matriz 3x3
(matriz quadrada)

6. Genericamente...
a11 a12 a13 a14 
a 21
A3×=  a 22 a 23 a 24 
4 
a 31

a 32 a 33 a 34 


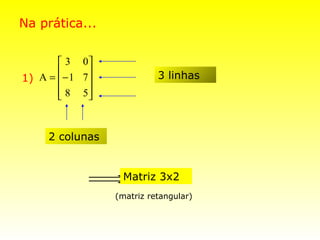
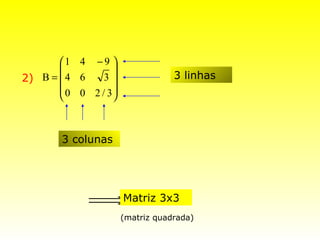
7. Matrizes Especiais
Matriz Linha
Ex: A = [ 3 -1 6 0]
1× 4
Matriz Coluna
0 
Ex: A=  9
3× 1
5 
 

9. Matriz Nula
Exs:
 0 0
1)A =  
2× 2  
 0 0
 0 0 0
2)B =
 0 0 0
2× 3
 

10. Na classe das matrizes quadradas
convém destacar:
 a11 a12 a13 
a
A =  21 a 22 
a 23 
 a 31
 a 32 a 33 

Diagonal Secundária Diagonal Principal
OBS:Diagonal Principal ⇒ elementos a ij com i= j

11. Matriz Triangular
Exs:
 2 0 0
 
1) A =  0 3 0
 −1 6 5
 
1 0 9 
2) B = 0 0 5 
 
0 0 - 1
 

12. Matriz Diagonal
Exs:
 2 0 0
 
1) A =  0 3 0
 0 0 0
 
9 0
2) B=
0 8

 

13. Matriz Identidade
Exs:
1 0
I2 = 
0 1

 
1 0 0
 
I3 =  0 1 0
0 0 1
 
1 0 0 0
 
I4 = 0 1 0 0
0 0 1 0
 
0 0 0 1
 

14. Matriz Transposta
Exs: 2 9 
2 3 4 
1) A=  ⇒ A t = 3 7 
2× 3 9 7 − 6 3× 2  
 4 − 6
 
1 0 0 1 -1 7 
   
2) B =  -1 3 8 ⇒ t
B = 0 3 6
3× 3  3× 3 
7 6 3 0 8 3 

15. Matriz Simétrica
É toda matriz quadrada A tal que A = At
1 4 0 1 4 0
   
Ex: A = 4 3 8 ⇒ t
A = 4 3 8
0 8 3 0
   8 3

16. Exercício
Obter a matriz A = (a ij ) 2×2 tal que a ij = 2i + j
 a11 a12 
a ij = 2i + j
A=
a 21 a 22 

a11 = 2.1 + 1 = 3
⇓ a12 = 2.1 + 2 = 4
a 21 = 2.2 + 1 = 5
3 4
A=
5 6
a 22 = 2.2 + 2 = 6
 

17. Igualdade entre matrizes
Para que duas ou mais matrizes sejam consideradas iguais elas devem
obedecer a algumas regras:
• Devem ter a mesma ordem, ou seja, o mesmo número de linhas
e o mesmo número de colunas.
• Os elementos devem ser iguais aos seus correspondentes.
Portanto, podemos concluir que:
A matriz A2 x 2 é igual a matriz B se, somente se, a matriz B
tiver também a ordem 2x2 e os elementos
a11 = b11 , a 21 = b21 , a12 = b12 e a 22 = b22

18. Veja um exemplo de matrizes:
As matrizes A e B são iguais, pois preenchem todos os requisitos
de igualdade de matrizes.

19. Encontre os valores numéricos de a, b, x e y sabendo que a igualdade
das matrizes abaixo é verdadeira.