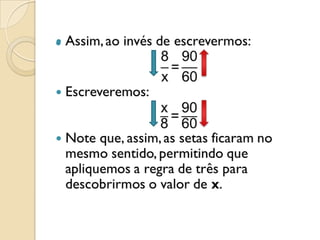
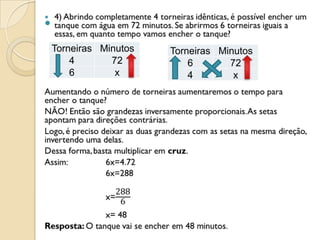
O documento apresenta os conceitos de proporção direta e inversa entre grandezas, explicando que na proporção direta as grandezas aumentam ou diminuem na mesma proporção, enquanto na proporção inversa uma grandeza aumenta quando a outra diminui. Fornece exemplos de grandezas direta e inversamente proporcionais e apresenta a regra de três para resolver problemas envolvendo proporções.

1. MATEMÁTICA
AULA 1 e 2 – REGRA DE TRÊS

2. PROPORÇÃO DIRETA
 Sabemos que uma proporção é direta
quando, tendo duas grandezas,
verificamos que:
◦ Aumentando uma grandeza a outra
também aumentará;
◦ Diminuindo uma grandeza a outra
também diminuirá.

3. PROPORÇÃO DIRETA
 Quanto maior for a o número de cópias,
maior será o custo em Euros.
◦ Ou seja, se aumentarmos a grandeza
número de cópias, aumentaremos também a
grandeza custo.

4. EXEMPLOS DE GRANDEZAS
DIRETAMENTE
PROPORCIONAIS
 Velocidade média e distância percorrida,
pois, se você dobrar a velocidade com que
anda, deverá, num mesmo tempo, dobrar a
distância percorrida.
 Área e preço de terreno. Quanto maior a
área, maior o preço.
 Altura de um objeto e o comprimento da
sombra projetada por ele. Quanto mais alto
o objeto, maior será a sombra projetada.

5. Proporção inversa
 Sabemos que uma proporção é
inversa quando, tendo duas
grandezas, verificamos que:
◦ Aumentando uma grandeza a outra
diminuirá;
◦ Diminuindo uma grandeza a outra
aumentará.

6. Proporção inversa
 Quanto maior a velocidade de um
automóvel, menor será o tempo que
ele levará para chegar ao lugar
determinado.
 Se a 180Km/h leva-se 20 segundos para
alcançar um objetivo, a 200 Km/h esse
mesmo objetivo será alcançado em 18
segundos.

7. EXEMPLOS DE GRANDEZAS
INVERSAMENTE
PROPORCIONAIS
 A Velocidade média e o tempo de viagem
são inversamente proporcionais, pois, se
você dobrar a velocidade com que anda,
mantendo fixa a distância a ser percorrida,
reduzirá o tempo do percurso pela metade.
 Número de torneiras de mesma vazão e
tempo para encher um tanque, pois, quanto
mais torneiras estiveram abertas, menor o
tempo para completar o tanque.

8. PROPORÇÃO DIRETA X INVERSA
 Imagine um grupo de pessoas que se
instale num acampamento que cobra R$
100,00 a diária individual.
◦ Uma pessoa gasta R$ 100,00 num dia, Duas
pessoas gastam R$200,00, ou seja,
aumentam as pessoas, aumentam os gastos.
Isso é proporção direta.
 Suponha que esse grupo disponha de
R$2.000,00 para gastos com estadia.
◦ Quanto maior o numero de pessoas, menor
será o tempo que permanecerão no
acampamento. Duas pessoas ficariam por 10
dias. Quatro pessoas por 5 dias. Isso é
proporção inversa.

9. RESUMINDO
 Duas grandezas são proporcionais se
elas se alteram com mesma medida,
mesma razão.
◦ São diretamente proporcionais se elas
têm a mesma tendência: quando uma
aumenta a outra também aumenta e
quando uma diminui a outra também
diminui.
◦ São inversamente proporcionais se elas
têm tendência inversa: quando uma
aumenta a outra diminui e quando uma
diminui a outra aumenta.

10. EXERCÍCIOS
 1) O número de acertadores e os prêmios são
grandezas diretamente ou inversamente
proporcionais?
 2) Sabendo que a, b, c e 120 são diretamente
proporcionais aos números 180, 120, 200 e 480,
determine os números a, b e c.
 3) Os números x, y e 32 são diretamente
proporcionais aos números 40, 72, 128. Determine
os números x e y.
Número de acertadores Prêmio
3 R$ 200.000,00
4 R$ 150.000,00

11. EXERCÍCIOS
 4) Diga se é diretamente ou inversamente
proporcional:
a) Número de pessoas em um churrasco e a
quantidade (gramas) que cada pessoa poderá
consumir.
b) A área de um retângulo e o seu comprimento,
sendo a largura constante.
c) Número de erros em uma prova e a nota obtida.
d) Número de operários e o tempo necessário para
eles construírem uma casa.
e) Quantidade de alimento e o número de dias que
poderá sobreviver um náufrago.

12. REGRA DE TRÊS
 Regra de três é o método de cálculo utilizado
quando sabemos o valor de três grandezas
para descobrirmos o valor de uma quarta
grandeza proporcional às três já conhecidas.
 Exemplo 1:
◦ Um carro percorre 900km em 6 horas. Quanto
ele percorrerá em 8 horas se manter a mesma
velocidade?
 Sabemos três grandezas e queremos saber
o quarto valor que é proporcional aos outros
três.
◦ Para isso basta dividirmos a distância percorrida
(900km)pela quantidade de horas (6 horas).

13.  Esse cálculo nos informará qual a distância
percorrida em uma hora. 900 dividido por 6
é igual a 150.
 Isso significa que em uma hora o carro
percorre 150km.
 Para sabermos o quanto ele percorrerá em
8 horas basta multiplicar esse valor (150)
por 8.
 Assim, teremos 8x150 que é igual a 1200.
 Logo, em 8 horas, mantendo a mesma
velocidade, o carro irá percorrer 1.200Km.
DIRETAMENTE
PROPORCIONAIS

14.  Note que nesse caso colocamos setas para
indicar a natureza da proporção, ou seja,
se ambas aumentam ou diminuem, são
proporcionais, o que é o caso.
 Em outras palavras, aumentando o número
de horas aumentará a distância percorrida.
 Como a proporção é direta, a fórmula
matemática seria assim escrita:
Grandeza 1 Grandeza 2
Tempo (horas) Distância (Km)
6 900
8 x

15. 

16. INVERSAMENTE
PROPORCIONAIS
 Exemplo 2:
◦ Um automóvel, com velocidade média de
90 Km/h, percorre certo espaço durante 8
horas. Qual será o tempo necessário para
percorrer o mesmo espaço com uma
velocidade de 60 Km/h?
 Primeiro é necessário descobrir se as
grandezas são diretamente ou
inversamente proporcionais.

17.  No exemplo anterior verificamos que
aumentando o tempo, aumentaríamos
também a distância percorrida, ou
seja, tínhamos grandezas diretamente
proporcionais.
 No presente exemplo, perguntamos:
Diminuindo a velocidade diminuiremos
o tempo de viagem?
 A resposta óbvia é:
 NÃO!
 Logo, temos grandezas inversamente
proporcionais.

18.  Observe no gráfico a diferença entre
as setas:
 Como as grandezas são inversamente
proporcionais, será necessário que
invertamos uma das grandezas para
que o cálculo resulte correto:
Grandeza 1 Grandeza 2
Tempo (horas)
Velocidade(Km/
h)
8 90
x 60

19. 

20. 

21. RESUMINDO


22. REGRA DE TRÊS COMPOSTA
 Essa regra é aplicada para as situações em
que temos mais de duas grandezas
proporcionais.
 Exemplo:
◦ Numa fábrica, 10 máquinas trabalhando 20
dias produzem 2000 peças. Quantas
máquinas serão necessárias para se
produzir 1680 peças em 6 dias?
Grandeza 1: Grandeza 2: Grandeza 3:
Número de
máquinas Dias
Número de
peças
10 20 2000
x 6 1680

23.  Para colocarmos as setas indicando se são
grandezas proporcionais diretas ou inversas,
é necessário perguntar:
 Aumentando o número de máquinas,
aumentaremos a quantidade de dias para
confeccionarmos determinado número de
peças?
◦ A resposta é NÃO, logo a seta tem que indicar
o sentido inverso ao da grandeza 1, pois são
inversamente proporcionais.Grandeza 1: Grandeza 2: Grandeza 3:
Número de
máquinas Dias
Número de
peças
10 20 2000
x 6 1680

24.  Aumentando o número de máquinas,
aumentaremos o número de peças
produzidas?
 A resposta é SIM, logo as grandezas
1e 3 diretamente proporcionais e as
setas devem indicar a mesma direção.
Grandeza 1: Grandeza 2: Grandeza 3:
Número de
máquinas Dias
Número de
peças
10 20 2000
x 6 1680

25. 
10 6 2000
x 20 1680

26. 

27. EXERCÍCIOS
 1) Um pedreiro é capaz de assentar 8 metros de muro por
dia. Quantos metros de muro esse pedreiro consegue
assentar em 15 dias?
 2) Uma máquina é capaz de produzir 6 réguas a cada dois
minuto. Quantas réguas essa máquina consegue produzir em
15 minutos?
 3) Marlene está lendo um livro com 352 páginas. Em 3 horas
ela já leu 48 páginas. Quanto tempo Marlene vai levar para
ler o livro todo?
 4) Abrindo completamente 4 torneiras idênticas, é possível
encher um tanque com água em 72 minutos. Se abrirmos 6
torneiras iguais a essas, em quanto tempo vamos encher o
tanque?

28. EXERCÍCIOS
 5) Um avião, à velocidade de 900 Km/h, leva 140
minutos para ir de Brasília a Porto Alegre. Se o mesmo
avião voasse a 750 Km/h, em quanto tempo faria a
mesma viagem?
 6) Funcionando durante 8 dias, 4 máquinas produziram
600 peças de uma mercadoria. Quantas peças dessa
mesma mercadoria serão produzidas por 6 máquinas
iguais às primeiras, se essas máquinas funcionarem
durante 12 dias?
 7) Se 5 homens podem arar um campo de 10 ha em 9
dias, trabalhando 8 horas por dia, quantos homens serão
necessários para arar 20 ha em 10 dias, trabalhando 9
horas por dia?

29. RESOLUÇÃO DOS
EXERCÍCIOS 1) Um pedreiro é capaz de assentar 8 metros
de muro por dia. Quantos metros de muro
esse pedreiro consegue assentar em 15
dias?
Aumentando a quantidade de
dias, aumenta a quantidade de
muros construídos?
SIM! Então são grandezas
diretamente proporcionais. As setas apontam a
mesma direção.
Logo, basta multiplicar em cruz.
Assim, x=8.15
x= 120
Resposta: 120 metros de muro em 15 dias.
Metros Dias
8 1
x 15

30. Réguas Minutos
6 2
x 15
RESOLUÇÃO DOS
EXERCÍCIOS

31. RESOLUÇÃO DOS
EXERCÍCIOS
Páginas Horas
352 X
48 3

32. 
Torneiras Minutos
4 72
6 x
Torneiras Minutos
6 72
4 x

33. 
Velocidade Minutos
900 140
750 x
Velocidade Minutos
750 140
900 x

34. 
Dias
Máquin
as Peças
8 4 600
12 6 x

35.  7) Se 5 homens podem arar um campo de 10 ha
em 9 dias, trabalhando 8 horas por dia, quantos
homens serão necessários para arar 20 ha em 10
dias, trabalhando 9 horas por dia?
Quanto mais homens, mais hectares arados?
SIM! Logo são grandezas proporcionais diretas.
Quanto mais homens, mais horas trabalham por dia?
NÃO! Logo são grandezas proporcionais inversas.
Quanto mais homens, mais dias trabalharam?
NÃO! Logo são grandezas proporcionais inversas.
Para realizarmos a Regra de Três todas as setas
devem apontar a mesma direção. Invertemos, então,
as grandezas, para deixarmos todas as setas na
Homen
s Hectares Dias
Hora
s
5 10 9 8
x 20 10 9
Homen
s Hectares Dias
Hora
s
x 20 9 8
5 10 10 9

36. 