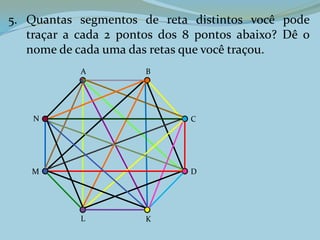
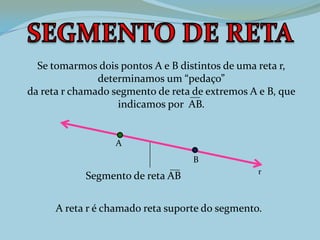
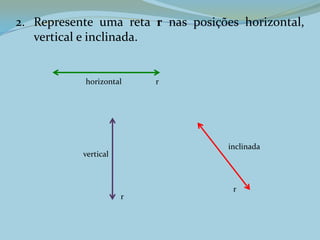
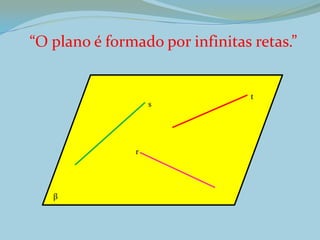
1. A geometria se baseia nos conceitos primitivos de ponto, reta e plano, que não podem ser definidos, mas sim entendidos por exemplos. 2. Um ponto não tem dimensão e é representado por uma letra maiúscula. Uma reta é formada por pontos alinhados e é representada por uma letra minúscula. 3. Um plano tem duas dimensões e é representado por uma letra minúscula do alfabeto grego.

2. A Geometria baseia-se em três noções:
Ponto
Reta
Plano
Essas noções são aceitas sem definição e, por
esse motivo, são chamadas de conceitos
primitivos.

3. O ponto não possui dimensões, isto é, não tem
comprimento nem largura ou altura.
Temos idéia do que é, mas não podemos defini-lo.
Um pequeno furo feito por um alfinete no papel, por
exemplo, nos dá a idéia de um ponto.
Nomeamos um ponto por uma letra maiúscula do
alfabeto latino.
A
B
C
D
E

4. Não podemos definir uma reta, no entanto, temos
noção do que seja. Por exemplo,
um risco no papel, feito com o auxílio de uma régua, nos
dá a idéia de uma reta.
Nomeamos uma reta por uma letra minúscula do alfabeto latino.
“A reta é formada por infinitos pontos alinhados.”
r
s

5. No desenho abaixo, o ponto B está entre o ponto A e o ponto C.
Entre o ponto B e o ponto C, conseguimos marcar outro ponto.
Entre esse novo ponto e o ponto C, conseguimos marcar outro.
Então, entre dois pontos sempre existe um terceiro ponto.
Quando vários pontos pertencem a uma mesma
reta eles são chamados
Pontos colineares.
Dois pontos sempre são colineares.
A B CD E F r

6. A RETA POSSUI APENAS
UMA DIMENSÃO, MAS
NÃO É POSSÍVEL MEDI-LA,
POIS ELA É INFINITA.

7. O piso de uma quadra poliesportiva nos dá a idéia de um plano.
Nomeamos um plano por uma letra minúscula do alfabeto
grego:
Alfa (α), beta (β), gama (γ), etc.
β

8. O PLANO POSSUI DUAS
DIMENSÕES: COMPRIMENTO
E LARGURA. NO ENTANTO,
NÃO É POSSÍVEL MEDI-LO.

9. “O plano é formado por infinitas retas.”
t
r
s
β

10. Quando várias retas estão contidas
num mesmo plano, elas são
chamadas
Retas coplanares.
Quando vários pontos pertencem a
um mesmo plano, eles são
chamados
Pontos coplanares.

12. 1. Vimos que ponto, reta e plano são noções elementares da geometria.
Escreva a idéia que nos dá cada situação descrita a seguir:
a) A marca da ponta do grafite em um papel.
b) Um fio bem esticado.
c) A superfície de uma mesa.
d) Um piso de uma quadra de basquete.
e) Estrelas no céu.
f) O encontro do chão com a parede.
g) Uma corda bem esticada.
h) A cabeça de um prego.
i) Uma folha de cartolina.
j) O fundo de uma piscina.
k) A linha de um caderno.
l) O piso de uma quadra de tênis.
m) A capa de um livro.
n) Uma caneta.
o) A cabeça de um parafuso.
p) A linha de um trem.
PONTO
PLANO
RETA
PLANO
PONTO
RETA
RETA
PONTO
PONTO
PLANO
PLANO
PLANO
RETA
PLANO
RETA
RETA

13. 2. A figura geométrica abaixo está representando quatro retas: r, s, t e u.
Determine:
a) Os pontos indicados que pertencem à reta r.
b) Os pontos indicados que pertencem à reta s.
c) Os pontos indicados que pertencem à reta u.
d) Os pontos que pertencem às retas r e s simultaneamente.
e) Os pontos indicados que pertencem à reta t.
f) Os pontos que pertencem às retas u e t simultaneamente.
A B
E D
B
EC A
B
C
DC
AB
CD
E
r
s
t
u

14. 3. Considerando as retas indicadas na figura, identifique:
a) As retas que passam pelo ponto A.
b) As retas que passam pelo ponto B.
c) A reta que passa por A e B.
d) A reta que passa por A e C.
e) A reta que passa por B e C.
r s
t s
s
r
t
r s
t
A
B C

15. 4. Responda usando uma das palavras ponto, reta ou plano.
a) Olhando o mapa do seu estado, você identifica a cidade onde você mora.
Qual é a idéia que você tem dessa representação?
b) Qual é a idéia que esta folha que você está lendo lhe traz?
c) Assistindo a uma partida de futebol, você observa a linha divisória do
campo. Qual a idéia que esta linha divisória lhe dá?
5. Desenhe uma reta, nomeie esta reta com a letra inicial do seu nome e faça
o que se pede:
a) Marque um ponto M que pertença à reta.
b) Marque dois pontos, P e Q, que não pertençam à reta.
PONTO
PLANO
RETA
M
P
Q

16. 6. Pontos colineares são os pontos que pertencem a uma mesma
reta. Utilizando essa informação, observe a figura abaixo e
responda:
a) Quais os pontos que pertencem à reta r?
b) Os pontos M, N e P são colineares?
c) Os pontos P, M e S pertencem à reta r?
d) Os pontos P, M e S são colineares?
P M N
SIM
NÃO
NÃO
r
P M N
S

17. 7. Quantas retas distintas você pode traçar a cada 2 pontos dos 6
pontos abaixo?. Dê um nome para cada reta.

18. 8. Quantas retas distintas você pode traçar a cada 2 pontos
dos 8 pontos abaixo? Dê o nome de cada uma das retas que
você traçou.

20. Vamos representar uma reta que passe pelos pontos A e B.
Se tentarmos representar, pelos mesmos pontos A e B,
uma outra reta diferente da que
acabamos de desenhar, não conseguiremos.
Pode tentar... Não é possível!
Então, podemos definir:
DOIS PONTOS DISTINTOS
DETERMINAM UMA ÚNICA RETA.
B
A

21. A reta que passa por dois pontos A e B
pode ser indicada por AB.
A
B
RETA AB

22. Todo ponto de uma reta r divide essa reta em duas regiões
opostas chamadas Semirretas.
r
semirreta
semirreta
A
B
O

23. O ponto de divisão é chamado origem da semirreta, e uma das semirretas, por
exemplo, é indicada por OA (lemos : “semirreta de origem O que passa por A”).
A reta r é chamada reta suporte das semirretas.
r
semirreta
semirreta
A
B
O

24. Se tomarmos dois pontos A e B distintos de uma reta r,
determinamos um “pedaço”
da reta r chamado segmento de reta de extremos A e B, que
indicamos por AB.
A reta r é chamado reta suporte do segmento.
r
A
B
Segmento de reta AB

26. 1. Quais segmentos de reta você observa em
cada figura?
A
B C
D
E
A B
C
DE
F
DE
CD
BC
AB
FA
EF
DE
CD
BC
AB

27. 2. Represente uma reta r nas posições horizontal,
vertical e inclinada.
r
r
r
horizontal
vertical
inclinada

28. 3. Identifique, em cada uma das figuras abaixo, as
retas desenhadas.
A
B
C
D
A B
C
D
E
AB
BC
CD
DA
AB
BC
CD
DE
EA
BD

29. 5. Quantas segmentos de reta distintos você pode
traçar a cada 2 pontos dos 8 pontos abaixo? Dê o
nome de cada uma das retas que você traçou.
A B
C
D
KL
M
N

30. 6. Quantas e quais as semirretas, com origem em P,
que estão representadas na figura?
P
A
B
C
E
D
PA
PB
PC
PD
PE
5 Semirretas

31. 7. Observe a figura e responda:
a) A reta tem origem?
b) A semi-reta tem origem?
c) O segmento tem origem?
d) A reta tem extremidade?
e) A semi-reta tem extremidade?
f) O segmento tem extremidade?
A
A
A
B
B
B
NÃO
SIM
NÃO
NÃO
SIM
SIM

32. 8. Indique as semi-retas representadas nas figuras
seguintes e que tem origem no ponto O.
AB
C D
O
O
OA
OB
OD
OC

33. 9. Quantas semirretas distintas você pode traçar a cada
2 pontos dos 4 pontos abaixo?. Dê o nome das semir-
retas.
A
GF
M
AM
MG
GF
FA
AG
MF FM
MA
GM
FG
AF
GA
12 SEMIRRETAS

34. 10. Observe as figuras I, II, III e IV.
Agora identifique pelo número:
a) Semirreta AB
b) Semirreta BA
c) Reta AB
d) Segmento AB
I
II
III
IV
A
A
A
A
B
B
B
B
II
IV
I
III