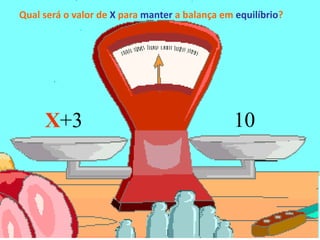
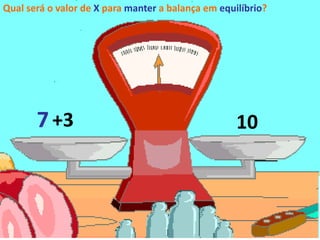
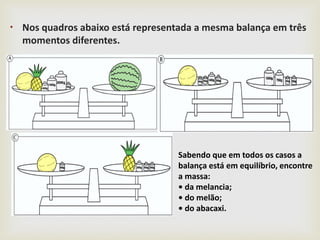
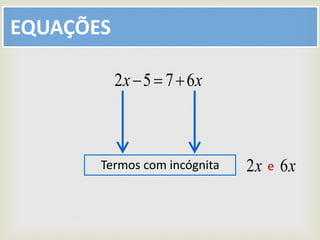
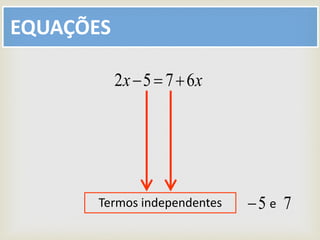
O documento descreve o conceito de equações matemáticas. Uma equação é definida como uma igualdade entre duas expressões onde pelo menos uma delas contém uma ou mais letras. Exemplos de equações são apresentados e os principais termos relacionados são explicados, como membros da equação, termos com incógnita e termos independentes.

1. Equações
Matemática 7º ano

2. Uma equação é uma igualdade entre duas
expressões onde, pelo menos numa delas,
figura uma ou mais letras.

3. EQUAÇÕES
Uma equação é uma igualdade entre duas expressões
onde, pelo menos numa delas, figura uma ou mais
letras.
xx 2483  22)56(3 
Exemplo:

4. EQUAÇÕES
Uma equação é uma igualdade entre duas expressões
onde, pelo menos numa delas, figura uma ou mais
letras.
xx 2483  22)56(3 
Exemplo:
Não é equaçãoÉ uma equação

5. 
Qual será o valor de X para manter a balança em equilíbrio?
X
Qual será o valor de X para manter a balança em equilíbrio?
X+3 10

6. 
Qual será o valor de X para manter a balança em equilíbrio?
7+3 10

7. 
• Nos quadros abaixo está representada a mesma balança em três
momentos diferentes.
Sabendo que em todos os casos a
balança está em equilíbrio, encontre
a massa:
• da melancia;
• do melão;
• do abacaxi.

8. EQUAÇÕES
À esquerda do sinal = de uma equação
encontra-se o 1º membro.
xx 4295 

9. EQUAÇÕES
À direita do sinal = de uma equação
encontra-se o 2º membro.
À esquerda do sinal = de uma equação
encontra-se o 1º membro.
xx 4295 

10. EQUAÇÕES
xx 6752 
Termos

11. EQUAÇÕES
xx 6752 
Termos com incógnita xx 62 e

12. EQUAÇÕES
xx 6752 
Termos independentes 75 e

13. EQUAÇÕES
xx 6752 
Resolver a equação é encontrar o valor (ou os
valores) que tornam a igualdade verdadeira. A
cada um desses valores chama-se raiz ou
solução da equação.

14. EQUAÇÕES
xx 6752 
Vejamos que é solução da equação…3
)3(675)3(2 Substituindo na equação
o x por tem-se…3

15. EQUAÇÕES
xx 6752 
Vejamos que é solução da equação…3
)3(675)3(2 
18756 
Substituindo na equação o
x por tem-se…3
…efectuando as operações
obtêm-se…

16. EQUAÇÕES
xx 6752 
Vejamos que é solução da equação…3
)3(675)3(2 
18756 
1111 
Substituindo na equação o
x por tem-se…3
…efectuando as operações
obtêm-se…
…no final fica-se com uma
proposição verdadeira…

17. EQUAÇÕES
xx 6752 
Vejamos que é solução da equação…3
)3(675)3(2 
18756 
1111 
…logo, é uma raiz ou solução da equação.3
Substituindo na equação o x
por tem-se…3
…efectuando as operações
obtêm-se…
…no final fica-se com uma
proposição verdadeira…

18. Equações sem parênteses e sem denominadores
4365  xx
•Resolver uma equação é
determinar a sua solução.

 102 x
•efectuamos as operações.


2
10
2
2

x
•Dividimos ambos os membros
pelo coeficiente da incógnita.
Conjunto solução  5

 5x
•Determinamos a solução.

 4635  xx
•Numa equação podemos
mudar termos de um membro
para o outro, desde que lhes
troquemos o sinal
•Num dos membros ficam os
termos com incógnita e no
outro os termos independentes
“5” é a solução

19. EQUAÇÕES COM PARÊNTESES
• simplificação de expressões com parênteses:
•Sinal menos antes dos parênteses: Tiramos os parênteses
trocando os sinais dos
termos que estão dentro  53225322  xxxx
•Sinal mais antes dos parênteses: Tiramos os parênteses
mantendo os sinais que
estão dentro.
  15231523  xxxx
•Número antes dos parênteses: Tiramos os parênteses,
aplicando a propriedade
distributiva da
multiplicação  22661332  xxxx

20. EQUAÇÕES COM DENOMINADORES
     436 3
3
4
2
2
1 xx 

•Começamos por reduzir todos os
termos ao mesmo denominador.


12
412
12
6
12
6 xx 
 

12
412
12
66 xx 


 •Duas fracções com o mesmo
denominador são iguais se os
numeradores forem iguais. xx 41266 
•Podemos tirar os
denominadores desde que sejam
todos iguais.

12646  xx 
 182 x 
 9
2
18
x

21. Esta fração pode
ser apresentada da
seguinte forma 2
3
2
5
2
2
2
3

xx
Sinal menos antes de uma fracção
2
3523 

xx •O sinal menos que se encontra antes da fracção
afecta todos os termos do numerador.


1(2) (6) (3) (3)
22
1
8
3
21 xx




7
43
7
43
437
348234
334842





xxx
xx
xx




2
1
8
3
21 xx 

 •Começamos por “desdobrar” a
fracção que tem o sinal menos
antes.(atenção aos sinais!)
•Reduzimos ao mesmo
denominador e eliminamos os
denominadores.

22. EQUAÇÕES
Chamam-se equações equivalentes às
equações que têm as mesmas raízes, ou seja, o
mesmo conjunto-solução.

23. EQUAÇÕES
Chamam-se equações equivalentes às equações que
têm as mesmas raízes, ou seja, o mesmo conjunto-
solução.
Exemplo:
85 x
712 x

24. EQUAÇÕES
Chamam-se equações equivalentes às equações que
têm as mesmas raízes, ou seja, o mesmo conjunto-
solução.
Exemplo:
85 x
712 x
3xA solução da equação é:

25. EQUAÇÕES
Chamam-se equações equivalentes às equações que
têm as mesmas raízes, ou seja, o mesmo conjunto-
solução.
Definição:
Exemplo:
85 x
712 x
3x
3x
A solução da equação é:
A solução da equação é:

26. EQUAÇÕES
Chamam-se equações equivalentes às equações que têm
as mesmas raízes, ou seja, o mesmo conjunto-solução.
Definição:
Exemplo:
85 x
712 x
3x
3x
A solução da equação é:
A solução da equação é:
Ambas as equações têm a
mesma solução. Assim, são
equações equivalentes.

27. Exercícios Testa os teus conhecimentos
Equações
Incógnita
1º Membro
2º Membro
Termos com
incógnita
Termos
Independentes
75x 1243  mm725  zz

28. Exercícios Testa os teus conhecimentos
Equações
Incógnita
1º Membro
2º Membro
Termos com
incógnita
Termos
Independentes
75x 1243  mm725  zz
x
5x
7
x
7;5
z
z25
7z
zz ;2
7;5
m
43 m
12 m
mm 2;3
1;4 

29. Exercícios Testa os teus conhecimentos
Exercício 2: Resolve mentalmente cada uma das equações.
84 x
46  x
1013 x
1442 x
732  xx
xx 2624 
(A)
(B)
(C)
(D)
(E)
(F)

30. 84 x
46  x
1013 x
1442 x
732  xx
xx 2624 
(A)
(B)
(C)
(D)
(E)
(F)
Estas são as soluções. Confere se conseguiste acertar em todas.
4x
2x
3x
5x
4x
2x