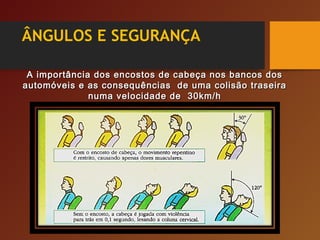
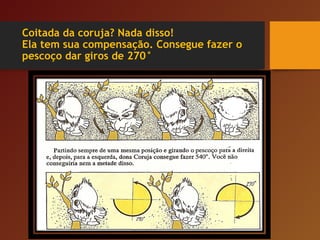
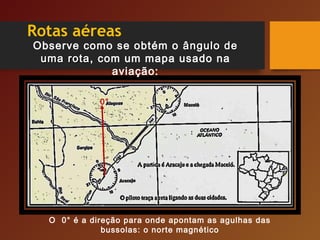
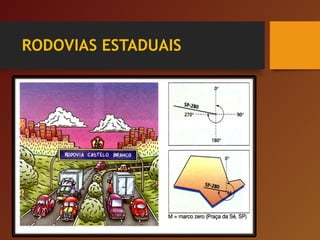
O documento discute vários tópicos relacionados a ângulos, incluindo: 1) a importância dos encostos de cabeça nos bancos de automóveis para proteção em colisões traseiras; 2) como os ângulos determinam a trajetória da bola de bilhar; 3) como ângulos de visão podem ser enganosos sobre a percepção de tamanho de objetos.

1. ÂNGULOS

2. ÂNGULOS E SEGURANÇA
A importância dos encostos de cabeça nos bancos dosA importância dos encostos de cabeça nos bancos dos
automóveis e as consequências de uma colisão traseiraautomóveis e as consequências de uma colisão traseira
numa velocidade de 30km/hnuma velocidade de 30km/h

3. Ângulos e o jogo de bilhar
Numa tacada, a bola segue uma trajetória constante: seuNuma tacada, a bola segue uma trajetória constante: seu
ângulo de chegada é sempre congruente ao ângulo de saída.ângulo de chegada é sempre congruente ao ângulo de saída.
Na tacada representada abaixo, em qual caçapa cairá aNa tacada representada abaixo, em qual caçapa cairá a
bola?bola?

4. Ângulo de visão
A diminuição do ângulo de visão nos dá a impressão que o
objeto diminuiu.

5. Observe como o
ângulo de visão pode
nos confundir

6. Ângulos formados de acordo
com a posição: futebol

9. Ângulo máximo de visão
50°50°
Você sabe qual é seuVocê sabe qual é seu
ângulo máximo de visão?ângulo máximo de visão?
As corujas tem os olhosAs corujas tem os olhos
fixos, por isso seufixos, por isso seu
ângulo de visão nãoângulo de visão não
chega a 50°chega a 50°
180°

10. Coitada da coruja? Nada disso!
Ela tem sua compensação. Consegue fazer o
pescoço dar giros de 270°

11. Rotas aéreas
Observe como se obtém o ângulo deângulo de
uma rotauma rota, com um mapa usado na
aviação:
O 0° é a direção para onde apontam as agulhas das
bussolas: o norte magnético
0°

12. RODOVIAS ESTADUAIS

13. Você poderá observar outrasVocê poderá observar outras
aplicações práticas, e perceberaplicações práticas, e perceber
porque o estudo dos ângulos é tãoporque o estudo dos ângulos é tão
importante na Geometria.importante na Geometria.

14. Definição
Duas semi-retas de mesma origem contidas em um
mesmo plano, dividem-no em duas regiões chamadas de
ângulos.
O
A
B
O é o vérticevértice do ângulo
As semirretas OA
e OB são os seus
ladoslados
α
Ângulo AÔB =
α

15. O GRAU

16. 1° = 60’ e 1’ = 60”

17. Uso do transferidor

18. Ângulo reto
Um ângulo é reto quando sua medida for de 90º.
O
A
B
m(AÔB) = 90º
O símbolo indica que
o ângulo é reto.

19. Ângulo raso
Um ângulo é raso quando sua medida é 180°
A O B
m(AÔB) = 180°

20. Ângulo obtuso
Todo ângulo maior que o reto e menor que o
raso é chamado ângulo obtuso.
O
A
B
O ângulo AÔB = β é obtusoobtuso
90º < β < 180º
β

21. Ângulo agudo
Todo ângulo não-nulo menor que o reto é
chamado ângulo agudo.
O
A
B
O ângulo AÔB = α é
agudo.
0º < α < 90º
α

22. Classificação
classificação medida representação
Nulo 0°
Agudo 0º < α < 90º
Reto 90°
Obtuso 90º < β < 180º
Raso 180°

23. Ângulos adjacentes
Se dois ângulos consecutivos não possuem, além do
lado comum, outros pontos comuns, dizemos que
eles são adjacentes.
O
A
C
B
AÔB e BÔC são adjacentesadjacentes
Apenas o lado OB é
comum aos dois ângulos

24. Ângulos complementares
• Dois ângulos são complementares quando a
soma de suas medidas for igual a 90º.
O
β
Os ângulosOs ângulos αα ee ββ sãosão ADJACENTESADJACENTES
COMPLEMENTARES.
α + β = 90º
α

25. Ângulos suplementares
• Dois ângulos são suplementares quando a soma
de suas medidas for igual a 180º.
O
α
Os ângulos α e β são ADJACENTES
SUPLEMENTARES.
α + β = 180º
β

26. Bissetriz de um ângulo
Chama-se bissetriz de um ângulo a semi-reta contida
no ângulo, de origem no seu vértice e que o divide
em dois ângulos adjacentes congruentes.
O
α
A semirreta Ox é a bissetrizbissetriz do ângulo
AÔB.
β
A
B
x
α = β

27. Retas perpendiculares
Retas concorrentes formando ângulos retos

28. RETAS OBLÍQUAS
SÃO RETAS CONCORRENTES QUE NÃO FORMAM
ÂNGULOS RETOS

29. Qual o menor ângulo formado pelos
ponteiros do relógio às 8:20h?

30. • O giro completo dos ponteiros de um relógio
descreve um ângulo de 360°.
• Como um relógio apresenta 12 divisões,
concluímos que o ângulo formado em cada
divisão é 360° : 12 = 30°.
30°

31. A diferença está no tempo em que cada
um dos ponteiros leva para fazer esse giro:
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
O ponteiro maior, dos minutos, em
1 hora (60 minutos), gira 360°
O ponteiro menor, das horas, em
1hora (60 minutos) gira 30°

32. Á primeira vista, faríamos 4 . 30° = 120°
Mas......
12
1
2
3
4
5
6
7
8
9
10
11
x α
α = 120° + x
20 min = 1
60 min 3
α = 120° + 10°
α = 130°
8:20h
1 . 30° = 10°
3

33. Exercícios do livro pgs: 12 e 13

34. Referências:
• IEZZI, Gelson; MACHADO, Antonio;
DOLCE, Osvaldo. Geometria Plana-
Conceitos básicos. 1ª edição. São
Paulo: Atual, 2008.
• JORGE, Sonia. Desenho Geométrico:
ideias e imagens. 3ª edição. São Paulo:
Saraiva, 2003.
• IMENES, Luiz Marcio; JAKUBOVIC,
José; LELLIS, Marcelo. Pra que serve a
Matemática? Ângulos. 6ª edição. São
Paulo: Atual, 1992.
• GIOVANNI, José Rui; PARENTE,
Eduardo. Aprendendo Matemática. São
Paulo: FTD, 2007