1. PROF. NILO

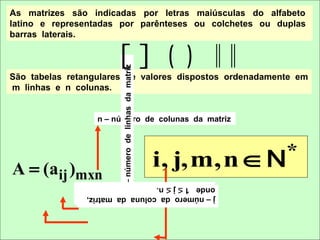
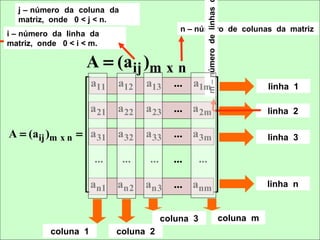
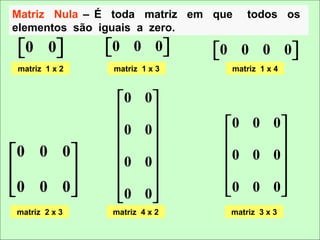
2. As matrizes foram utilizadas
pela primeira vez pelo
matemático e advogado
inglês James Sylvester que
definiu Matriz como “arranjo
oblongo de termos”.
Seu colega também inglês
Arthur Cayley instituiu
algumas operações básicas
entre as matrizes, em
“Memoir on the Theory of
Matrices”, em 1858.
A multiplicação matricial
deveu-se ao matemático
alemão Gotthold Eisenstein,
considerado por Gauss, um
matemático do mesmo nível
que Newton e Arquimedes.

3. São tabelas retangulares
de valores dispostos
ordenadamente em linhas
e colunas.
Dentre suas
aplicações podemos
citar:
armazenamento e
manipulação de
informações
tabuladas e as
ferramentas para
transmissão de
imagens e sons
digitalizados pela
internet.

4. As matrizes são indicadas por letras maiúsculas do alfabeto
latino e representadas por parênteses ou colchetes ou duplas
barras laterais.
 
  ( )
m – número de linhas da matriz
São tabelas retangulares de valores dispostos ordenadamente em
m linhas e n colunas.
n – número de colunas da matriz
*
A = (aij )mxn i, j,m,n ∈N
onde 10≤≤j i≤≤n.
onde m.
j i––número da colunada matriz,
número da linha da matriz,

5. j – número da coluna da
m – número de linhas
matriz, onde 0 < j < n.
n – número de colunas da matriz
i – número da linha da
matriz, onde 0 < i < m.
A = (aij )m x n
 a11 a12 a13 ... a1m  linha 1
 
a ... a 2m 
21 a 22 a 23 linha 2
 
 
A = (aij )m x n =  a 31 a 32 a 33 ... a 3m  linha 3
 
 ... ... ... ... ... 
 
an1 an2
 an3 ... anm  linha n
coluna 3 coluna m
coluna 1 coluna 2

6. EXEMPLO 01
Dada a matriz A = (aij)3x2 através de sua lei de
formação, escreva essa matriz.
 i + j , se i ≤ j

aij = 
 i − j , se i > j

SOLUÇÃO
 a11 a12   2 3 
   
A = (aij )3 x 2 = a 21 a 22  =  1 4 
   
   
a 31 a 32   2 1 

7. EXEMPLO 02
Uma indústria automobilística produz três modelos
de veículos empregando diferentes peças para a
montagem do motor. Na matriz abaixo, cada
elemento aij representa a quantidade de peças
do tipo j utilizada na fabricação de um veículo
modelo i. 15 10 12 
 
A = 10 11 13 
 
 
14 12 11
a) Quantas peças do tipo 1 serão utilizadas para
fabricar um veículo do modelo 2?
b) Quantas peças de cada tipo são necessárias para
fabricar oito veículos modelo 1, três veículos
modelo 2 e dois veículos modelo 3?

8. Matriz Linha – É toda matriz com apenas 1 linha,
ou seja, é toda matriz do tipo 1 x n.
 −1 4
   3 −2 0 
  0 3 2 π
 
matriz 1 x 2 matriz 1 x 3 matriz 1 x 4
Matriz Coluna – É toda matriz com apenas 1
coluna, ou seja, é toda matriz do tipo n x 1.
4  6 
3    
  0  −2 
   
 −5 
   
   1 
 −7   
matriz 2 x 1 matriz 3 x 1  3
  matriz 4 x 1

9. Matriz Nula – É toda matriz em que todos os
elementos são iguais a zero.
0 0
  0 0 0 
  0 0 0 0 
 
matriz 1 x 2 matriz 1 x 3 matriz 1 x 4
0 0
 
0 0 0 0 0
   
0 0 0   0 0 0
  0 0  
0 0 0    
  0
 0
 0 0 0
matriz 2 x 3 matriz 4 x 2 matriz 3 x 3

10. Matriz Quadrada de ordem n – É toda matriz do
tipo n x n, isto é, que possui igual número de
linhas e colunas.
 a11 a12 a13 ... a1n 
 
a ... a 2n 
21 a 22 a 23
 
 
A = (aij )m x n =  a 31 a 32 a 33 ... a 3n 
 
 ... ... ... ... ... 
 
an1 an2
 an3 ... ann 
Diagonal Principal Diagonal Principal
( i+j = n+1) ( i = j)

11.  2 −1  3 − 2 0   6 − 2 −1 5 
     
4 3   5 1 −3   0 3 2 −3 
     
  5 1 2 4
 −6 0 2  
 
 −2 3 4 0 
 

12. Matriz Triangular – É toda matriz quadrada
composta apenas de zeros nos elementos acima
ou abaixo da diagonal principal.
 3 −2 5   3 0 0
   
 0 1 −3   4 1 0
   
   
0 0 2  −2 5 6 
Triangular Superior Triangular Inferior

13. Matriz Diagonal – É toda matriz quadrada em que
os elementos que não pertencem à diagonal
principal são iguais a zero.
 2 0 4 0 0 5 0 0
     
 0 3  0 −2 0  0 2 0
     
   
0 0 5 0 0 0
 0 0
 
 0 0
 

14. Matriz Identidade ( ou Unitária ) – É toda matriz
diagonal, com ordem igual ou superior a 2, em
que os elementos da diagonal principal são iguais
a 1.
1 0
I2 =  
0 1 1 0 0
    1 0 0 0
I 3 = 0 1 0  
  0 1 0 0
  I4 =  
0 0 1  
0 0 1 0
 
0
 0 0 1


15. Dadas duas matrizes A = (aij)mxn e B = (bij)pxq ,
essas matrizes serão iguais quando as matrizes
forem da mesma ordem e todos os elementos
correspondentes de uma e outra forem iguais.
 4 2  4 2
 =  ambas são 2 x 2
 −1 3   −1 3 
    são iguais
 5 − 1 3   5 −1 3 
   
 0 4 2 ≠ 0 4 1 ambas são 3 x 3
   
    não são iguais
 2 − 3 1   2 −3 1 

16. EXEMPLO 03
Determine x, y, z e t, para que se tenha:
 x 2 y   25 −4 
   
 
 10 3z  = 10 9 
 
   
 4x t   20 − t 
 
SOLUÇÃO
As duas matrizes são de ordem 3 x 2. Falta agora
fazer a igualdade entre os termos correspondentes.
 x=5
 ; 4x = 20 ⇒ x = 5
2
x = 25 ⇒ x = ± 25 = ±5 
 x = −5
 ; t = − t ⇒ 2t = 0 ⇒ t = 0
y = −4 ; 10 = 10 ; 3z = 9 ⇒ z = 3

17. EXEMPLO 04
Calcule a soma de
matrizes abaixo.
Soma de Matrizes – É uma
operação de soma dos  6 3   2 −4 
elementos correspondentes    
de duas matrizes de 10 4  +  −1 0 
   
mesma ordem, gerando    
uma nova matriz de mesma  5 1   10 −1
ordem.
SOLUÇÃO  8 − 1
As duas matrizes são de ordem
 
3 x 2. Então a soma é 9 4
 
 
15 0 

18. I ) A+(B+C)=(A+B)+C
Enfermeira, estou
com febre !
II ) A + B = B + A
III) A + 0 = 0 + A
IV) A + (−A) = −A + A = 0

19. Multiplicação de Escalar por Matriz – É uma
operação similar a uma soma de matrizes, onde
todas essas matrizes são iguais. Portanto, basta
multiplicar o escalar por cada elemento da matriz.
EXEMPLO 05
Calcule o resultado SOLUÇÃO
da multiplicação de
escalar por matriz  2 −1 3   10 −5 15 
indicada abaixo. 5.  = 
 6 4 −2   30 20 −10 
   
 2 −1 3 
5.  
 6 4 −2 
 

20. I ) ( λ. µ ).A = λ.(µ.A)
II ) ( λ + µ ).A = λ.A + µ.A
III) ( λ − µ ).A = λ.A − µ.A
IV) λ.( A + B ) = λ.A + λ.B
V) 1 A = A

21. Oposta de Matriz – É obtida multiplicando o escalar
−1 pela matriz dada.
EXEMPLO 06
Calcule o resultado SOLUÇÃO
da multiplicação de
escalar por matriz  3 − 1   −3 1 
indicada abaixo.    
 −4 2   4 −2 
 3 −1 ( −1).  = 
     
 5 0   −5 0 
 −4 2 
( −1).      
   2 −3   −2 3 
   
 5 0
 
 2 −3 
 

22. Subtração de Matrizes – É uma operação de soma
de uma matriz com a oposta da segunda.
EXEMPLO 07
Calcule o resultado SOLUÇÃO
da diferença de
matrizes indicada
 6 3   2 −4   4 7 
abaixo.      
10 4  −  −1 0  =  11 4 
 6 3   2 −4       
         
10 4  −  −1 0   5 1   10 −1  −5 2 
   
   
 5 1   10 −1

23. Produto de Matrizes – Dadas duas matrizes A
= (aij)m x n e B = (bij)p x q , chama-se produto das
matrizes A e B, a matriz C = (cij)m x q , onde só é
possível efetuar essa operação se n = p.
A ordem da matriz produto é obtida pelo número
de linhas da primeira matriz e o número de
colunas da segunda matriz.
Só é possível efetuar o produto de duas matrizes,
se o número de colunas da primeira for igual ao
número de linhas da segunda.

24. I ) ( A.B ).C = A.( B.C )
II ) ( A + B ).C = A.C + B.C
III) C.( A + B ) = C.A + C.B
IV) ( α.A ).B = A .(α.B ) = α (A.B) onde α ∈ IR
V) A.B ≠ B.A , em geral. Se A.B = B.A, então A e B
comutam.
VI) Se A.B = 0, não é necessário que A = 0 ou
B = 0, porém se A.B = 0, qualquer que seja B, então
A = 0. Da mesma forma se A.B = 0, qualquer que
seja A, então B = 0.

25. EXEMPLO 08 SOLUÇÃO
Calcule o resultado da  1 − 1 Matriz
diferença de matrizes   1 2 3 Produto
indicada abaixo. 2 2  .   é 3x
 1 − 1    4 −5 1  3
Produto
  1 2 3    
2 2  .  3 4 
 possível
   4 −5 1  3x2 2x3
   
=
3 4 
1 1 1 2 1 3
−1 4 −1 −5 −1 1
Matriz −3 7 2
Produto 2 1 2 2 2 3
é da 10 −6 8 2 4 2 −5 2 1
forma:
3 1 3 2 3 3
19 −14 13
4 4 4 −5 4 1

26. 0
A = In
1
A =A
2
A = A.A
3
A = A.A.A
n
A = A.A.A....A

27. EXEMPLO 09
Dada a matriz A abaixo, calcule A0 , A2 e A3.
 4 2 SOLUÇÃO
A= 
 −1 3  1 0
  A0 = I 2 =  
0 1
 
 4 2   4 2   14 13 
A 2 = A.A =  . = 
 − 1 3   − 1 3   −7 7 
     
 14 13   4 2   43 −11
A 3 = A 2 .A =  . = 
 −7 7   −1 3   −35 7 
     

28. EXEMPLO 10
Dada a matriz A abaixo, calcule A1 + A2 + A3 + ... + A200.
1 0  SOLUÇÃO
A= 
1 0  1 0  1 0
1 0 
  A 2 = A.A =  . = 
A matriz A é IDEMPOTENTE. 
1 0  1 0  1
    0

1 0  1 0  1 0 
A 3 = A 2 .A =  . = 
1 0  1 0  1 0 
     
1 0  1 0  1 0 
A 200 =  . = 
1 0  1 0  1 0 
     
1 0   200 0
A1 + A 2 + ... + A 200 = 200.  = 
1 0   200
   0


29. EXEMPLO 11
Uma indústria fabrica certa máquina em dois
modelos diferentes, A e B. O modelo A utiliza
4 condensadores, 3 interruptores e 7 válvulas; o
modelo B utiliza 3 condensadores, 2 interruptores e
9 válvulas. Em novembro, foram encomendadas 3
máquinas do modelo A e 2 do modelo B; e em
dezembro, 2 máquinas do modelo A e 1 do modelo
B.
Qual o número de condensadores, interruptores e
válvulas em cada um dos meses para fabricar essas
encomendas?
SOLUÇÃO
Sugestão: monte primeiramente uma tabela peças x modelos e
posteriormente monte uma tabela modelo x meses.

30. Transposição de Matrizes – Dada uma matriz
A = (aij)m x n sua transposta é a matriz At = (aji)n x m.
Na prática é a operação de troca de posição dos
elementos da linha i para a coluna i.
EXEMPLO 12
Obtenha a transposta SOLUÇÃO
da matriz abaixo.
 6 −2 
 6 −3 2 1 
A=   
 −2 4 0 −4   −3 4 
 
At =  
 
2 0
 
 1 −4 
 

31. Matrizes Simétrica – É uma matriz
em que A = At, isto é, uma a b c
matriz em que os elementos a b  
  ; b d e
dispostos simetricamente em b
 d 
 

relação à diagonal principal são 
c e f
iguais.
Matrizes Anti-Simétrica – É uma
matriz em que A = −At, isto é,
uma matriz em que os 0 a b
elementos dispostos 0 a  
  ;  −a 0 c
simetricamente em relação à −a
 0 
 

diagonal principal são simétricos. 
−b −c 0
Os elementos da diagonal
principal são iguais a zero.

32. I ) ( A + B )t = At + Bt
II ) ( λ.A )t = λ.At Cuidado com a
Propriedade V,
III) (At)t = A que ela induz
ao erro !
IV) (−A)t = −At
V) (A.B)t = Bt.At

33. Determinante de uma Matriz – Considerando apenas
as matrizes quadradas M de elementos reais, o
determinante dessa matriz quadrada, representada
por det M, será o número obtido pela operação de
seus elementos da seguinte forma:
Se a matriz quadrada é de ordem n = 1, temos:
M = a11  ⇒ det M=det a11  = a11 = a11
   
Se a matriz quadrada é de ordem n = 2, temos:
 a11 a12   a11 a12 
M=  ⇒ det M=det  =
a a 22  a a 22 
 21   21 
a11 a12
= = a11 .a 22 − a12 .a 21
a 21 a 22
− +

34. Se a matriz quadrada é de ordem n = 3, temos:
 a11 a12 a13   a11 a12 a13 
   
M = a 21 a 22 a 23  ⇒ det M=det a 21 a 22 a 23  =
   
   
a 31 a 32 a 33  a 31 a 32 a 33 
a11 a12 a13 a11 a12
= a 21 a 22 a 23 a 21 a 22 =
a 31 a 32 a 33 a 31 a 32
− − − + + +

35. = a11 .a 22 .a 33 + a12 .a 23 .a 31 + a13 .a 21 .a 32
− a13 .a 22 .a 31 − a11 .a 23 .a 32 − a12 .a 21 .a 33
Pierre Frédéric
Sarrus
(1789-1861)

36. Se a matriz quadrada é de ordem n natural, onde
n ≥ 4, aplicaremos o Teorema de Laplace, que
também é válido para determinantes de ordens 1,
2 e 3.
Para tanto, basta escolhermos uma
linha ou coluna do determinante e
calcular os somatórios dos produtos
dos elementos da fila escolhida
pelos respectivos co-fatores.
 a11 a12 ... a1j ... a1n 
Pierre Simon  
a ... a 2n 
Laplace 21 a 22 ... a 2j
(1749-1827) M= 
 
Físico,
 ... ... ... ... ... ... 
Astrônomo e  
Matemático an1 an2 ... an3 ... ann 
 

37. Vamos escolher uma coluna genérica j, teremos:
 a11 a12 ... a1j ... a1n 
 
a ... a 2n 
21 a 22 ... a 2j
M=


 j
 ...

...
an1 an2
... ...
... anj
... ... 
... ann 

det M = ∑ anj .Anj
  n =1
onde :
Anj = ( −1)n + j .Dnj
Determinante de ordem uma unidade
abaixo, obtido eliminando-se a linha e a
coluna onde se encontra anj.

38. Se escolhermos uma linha genérica i, teremos:
 a11 a12 ... a1n 
 
a ... a 2n 
21 a 22
 
  i
 ...
∑ ain .Ain
... ... ... 
M=  det M =
 ai1 ai1 ... ain 
  n =1
 ... ... ... ... 
 
a ... ann 
 n1 an2 
onde :
i+n
A in = ( −1) .Din
Determinante de ordem uma unidade
abaixo, obtido eliminando-se a linha e a
coluna onde se encontra anj.

39. EXEMPLO 13
Calcule o valor dos determinantes das matrizes
abaixo.
2 1 3
 3 2  
a)A =   b)B =  1 4 2
1 4  
   
5 3 1
1 2 3 −4 2 
 
2 4 2 4 0 1 0 0 0
   
0 1 1 0  
d)D =  0 4 0 2 1
c)C =  
   
1 0 2 3  0 −5 5 1 4
   
3
 0 1 0
 0 1
 0 −1 2 


40. Inversão de Matrizes – Se A é uma matriz quadrada
de ordem n, dizemos que A é matriz inversível se
existir uma matriz B tal que A.B = B.A = In.
Dada uma matriz
inversível M, chama-se
inversa de A, a matriz M−1
, que é única, tal que
M. M−1 = M−1 .M = In.
Quando uma matriz M
não é inversível, ela é
dita matriz singular.

41. I ) (A−1)−1 = A
II ) A matriz unidade é a sua própria inversa.
III) (α.A)−1 = (1/α). A−1
Se A e B são matrizes quadradas de mesma
ordem, temos:
IV) ( α.A ).B = A .(α.B ) = α (A.B) onde α ∈ IR
V) A.B ≠ B.A , em geral. Se A.B = B.A, então A e B
comutam.

42. Lembrando que M. M−1 = In.
Por meio de determinantes, temos:
M−1 é a matriz M invertida.
1
. ( M ')
−1 t det M é o determinante da
M =
det M matriz M a inverter.
(M’)t é a matriz de
cofatores transposta de M.
Por meio de operações elementares.

43. EXEMPLO 12
Obtenha a matriz inversa das matrizes abaixo,
pelos 3 processos.
1 0 2
1 2  
a)A =   c)C =  2 1 3 
3 4  
   
3 1 0
1 4 7
 
 3 6
b)B =   d)D =  2 5 8 
 
 2 4
   
 3 6 9

44. SOLUÇÃO I
−1 1 2 x z 
A.A = I2 ⇒   .A −1 = I 2 A −1 =  
3 4 y w 
 
 
2x2 2x2 2x2
 1 2  x z   1 0  x + 2y z + 2w   1 0 
  . = ⇒  = 
 3 4  y w   0 1
       3x + 4y 3z + 4w   0 1 
   
AGORA É
SÓ
RESOLVER
OS
SISTEMAS

45.  1 2  x z   1 0  x + 2y z + 2w   1 0 
  . = ⇒  = 
 3 4  y w   0 1
       3x + 4y 3z + 4w   0 1 
   
 x + 2y = 1
  z + 2w = 0

 
 3x + 4y = 0
  3z + 4w = 1

1 2 1 1 2 0
3 4 0 3 4 1
−2 −3 −2 1
y = 3/2 w = −1/2
x = −2 z=1
 x z   −2 1 
A −1 =  = 
 y w   3 / 2 −1/ 2 
   

46. SOLUÇÃO II
1 1
. ( M ') . ( A')
−1 t −1 t
M = A =
det M det A
1 2 1 2
A=  ;det A = = 1.4 − 2.3 = −2
3 4
  3 4
A11 = ( −1)1+1 . 4 = 4 A12 = ( −1)1+ 2 . 3 = −3
A 21 = ( −1)2+1 . 2 = −2 A 22 = ( −1)2+ 2 . 1 = 1
 4 −3   4 −2 
A' =   ⇒ (A')t =  
 −2 1 
   −3 1 
 
1  4 −2   − 2 1 
A −1 = . = 
−2  −3 1   3 / 2 −1/ 2 
   

47. SOLUÇÃO III
1 2 1 2 1 0 L1 = 2.L1 − L2  − 1 0 2 − 1
A= ⇒    
 3 4  3 4 0 1
   3 4 0 1
  
L2 = L2 + 3.L1
 − 1 0 2 −1  L1 = − L1  1 0 −2 1 
   
 0 4 6 −2 
 
L4 = L4 : 4  0 1 3 / 2 − 1/ 2 
 
PERCEBERAM QUE
OS RESULTADOS
BATERAM ?

48. Está caindo
uma chuva de
Matrizes e
Determinantes!