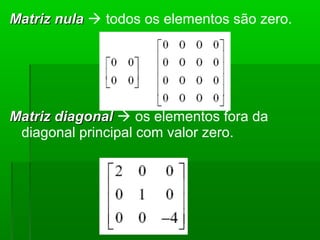
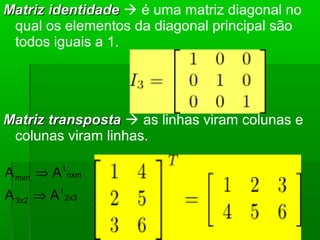
O documento introduz o conceito de matrizes, definindo-as como tabelas de elementos dispostos em linhas e colunas. Explica diferentes tipos de matrizes como matrizes quadradas, nulas, diagonais e identidade. Também descreve operações básicas com matrizes como adição, subtração, multiplicação por escalar e produto entre matrizes.

1. INTRODUÇÃO AINTRODUÇÃO A
MATRIZESMATRIZES
Prof. HenriqueProf. Henrique

2. Definição:Definição:
 Chamamos de matriz a uma tabela de elementosChamamos de matriz a uma tabela de elementos
dispostos em linhas e colunas.dispostos em linhas e colunas.
 Exemplo:Exemplo:
 Ao abstrairmos osAo abstrairmos os
significados das linha esignificados das linha e
colunas, obtemos acolunas, obtemos a
matriz:matriz:

3. mxnij
mnm3m2m1
3n333231
2n232221
1n131211
mxn ]a[
aaaa
aaaa
aaaa
aaaa
A =
















=





 Representação de uma matriz genérica:Representação de uma matriz genérica:
LINHA
COLUNA
ELEMENTOS

4. Matrizes EspeciaisMatrizes Especiais
Matriz QuadradaMatriz Quadrada
 quando o número de linhas é igual aoquando o número de linhas é igual ao
número de colunas (m=n).número de colunas (m=n).
Exemplo:Exemplo:
2221
1211
2x2
aa
aa
A =
Diagonal
Principal
Diagonal
Secundária

5. Matriz nulaMatriz nula  todos os elementos são zero.
Matriz diagonalMatriz diagonal  os elementos fora da
diagonal principal com valor zero.

6. Matriz identidadeMatriz identidade  é uma matriz diagonal no
qual os elementos da diagonal principal são
todos iguais a 1.
Matriz transpostaMatriz transposta  as linhas viram colunas e
colunas viram linhas.
2x3
t
3x2
nxm
t
mxn
AA
AA
⇒
⇒

7. Igualdade de matrizesIgualdade de matrizes
Dadas duas matrizes de mesma ordem
A = (aij) e B = (bij), dizemos que:
A = B ⇔ aij = bij

8. Operações comOperações com
matrizes:matrizes:
Adição e Subtração de matrizesAdição e Subtração de matrizes
Essas operações só podem ser feitas com
matrizes de mesmo número de linhas e
mesmo número de colunas.
Sejam duas matrizes Am×n e Bm×n.

10. Multiplicação entre um númeroMultiplicação entre um número
real e uma matrizreal e uma matriz
ℜ∈∀= ααα ).(. ijaA






=





35300
10515
760
213
5.

11. Produto entre matrizesProduto entre matrizes
Existe o produto entre matrizes, Am×n e Bn×p, se
somente se, duas matrizes tais que o número de
colunas da primeira (n) é igual ao número de
linhas da segunda (n).

12. Exemplo:Exemplo:
A3x2 . B2x2 = C3x2










=










++
++
++
==






=










=
2422
13
1412
5.44.15.24.3
0.41.10.21.3
3.42.13.22.3
A.BC
42
13
Be
54
01
32
A

13. 









=





=
65
43
21
Be
654
321
A
A2x3.B3x2 = C2x2
c11 = 1 x 1 + 2 x 3 + 3 x 5 = 1 + 6 + 15 = 22
c12 = 1 x 2 + 2 x 4 + 3 x 6 = 2 + 8 + 18 = 28
c21 = 4 x 1 + 5 x 3 + 6 x 5 = 4 + 15 + 30 = 49
c22 = 4 x 2 + 5 x 4 + 6 x 6 = 8 + 20 + 36 = 64






=
6449
2822
C

14. Propriedades daPropriedades da
multiplicaçãomultiplicação
1) AB ≠ BA
Embora existam matrizes M e N, tais que
MN = NM, neste caso dizemos que elas comutam
entre si.
2) (AB) C = A (BC)
3) A (B + C) = AB + AC e (A + B)C = AC + BC
4) A. 0 = 0. A = 0
5) A. I = I. A = A
6) (AB)t
= Bt
. At