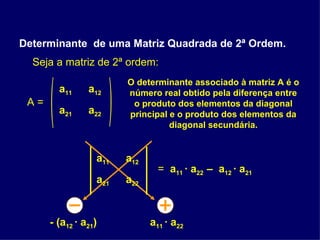
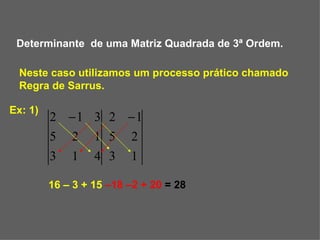
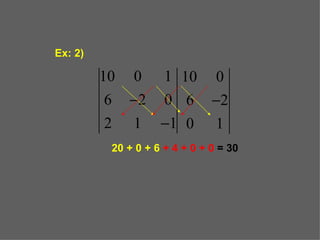
O documento explica o que é um determinante e como calculá-lo para matrizes quadradas de 1a, 2a e 3a ordem. O determinante é um número real associado à matriz e é calculado usando a diferença entre produtos de elementos nas diagonais principal e secundária para matrizes de 2a ordem ou a regra de Sarrus para 3a ordem. Propriedades incluem o determinante ser zero se houver linhas iguais ou proporcionais ou se uma linha for combinação linear de outras.

1. Determinantes

2. Determinantes Determinante é um número real associado a uma matriz quadrada. Notação: det A ou |A|. Determinante de uma Matriz Quadrada de 1ª Ordem. Seja a matriz A = (a 11 ). O determinante de A será o próprio elemento a 11 . A = ( 3 ) , logo | A | = 3

3. Determinante de uma Matriz Quadrada de 2ª Ordem. = a 11 · a 22 – a 12 · a 21 a 11 · a 22 - (a 12 · a 21 ) Seja a matriz de 2ª ordem: A = a 11 a 12 a 21 a 22 O determinante associado à matriz A é o número real obtido pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. a 11 a 12 a 21 a 22

4. Determinante de uma Matriz Quadrada de 2ª Ordem. Ex: 1) + - 7 2 3 5 = 7.5 - 2.3 = 29

5. Ex: 2)

6. Determinante de uma Matriz Quadrada de 3ª Ordem. Neste caso utilizamos um processo prático chamado Regra de Sarrus. Ex: 1) 16 – 3 + 15 –18 –2 + 20 = 28

7. Ex: 2) 20 + 0 + 6 + 4 + 0 + 0 = 30

8. Determinantes Propriedades

9. Casos em que um determinante é igual a ZERO: • Quando todos os elementos de uma fila são nulos Ex: 1) 2)

10. • Quando possui duas filas paralelas iguais ou proporcionais 3) 4) Casos em que um determinante é igual a ZERO:

11. • Quando uma das filas é a combinação linear de outras filas paralelas. 5) 6) Casos em que um determinante é igual a ZERO:

12. Outras propriedades: • det(A)=det(A t ) Ex: 1) 2)

13. 1) 2) Ex: • O determinante de uma matriz triangular é igual ao produto dos elementos da diagonal principal Outras propriedades:

14. 1) Ex: • Quando trocamos a posição de duas filas paralelas, o determinante troca de sinal 2) Outras propriedades:

15. Ex: 1) 2) • Se uma fila for multiplicada por um n o , então o determinante também fica multiplicado por esse n o Outras propriedades:

16. • det(k.A)=k n. det(A), onde n é a ordem de A 1) 2) Ex: Outras propriedades:

17. • det(A.B)=detA.detB Ex: Outras propriedades:

18. • det(A -1 )=1/detA Ex: