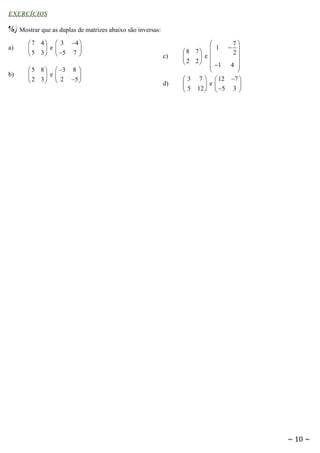A matriz é um conjunto numérico disposto em linhas e colunas. O documento explica os conceitos de matriz, incluindo matriz quadrada, linha, coluna, elementos, transposta e operações como adição. Há também exercícios para fixar os conceitos ensinados.

1. 10 - Matrizes
MATRIZES
Observe os seguintes conjuntos numéricos, onde os elementos estão dispostos em linhas e colunas e colocados
entre colchetes, parênteses ou barras duplas:
Exemplos:
1.
2.
1 0 2
A= 

4 3 5
0 5
B= 

 8 1
3.
4.
1 
C = 3
 
6
 
D = 2
3
4
Conjuntos desse tipo chamamos de matriz.
 As filas horizontais são chamadas linhas.
 As filas verticais são chamadas colunas.
Seja a matriz A: 1ª coluna 2ª coluna 3ª coluna

1ª linha 
2ª linha 

3ª linha 
4ª linha 


1
0
8
6
0
1
9
7
7
5
4
6
7
3








Ela possui 4 linhas e 3 colunas, assim é do tipo 4 × 3 (lê-se 4 por 3).
Observe:
Escrevemos primeiro o número de linhas e depois o número de colunas.
Exemplos:
1.
9 3 


1 4 
B= 
5
 0 3 


2 0 


2.

C= 3

5
3.

 8
D= 
7
5


7

0


é uma matriz do tipo 4 × 2
2
3
8

é uma matriz de ordem 1 × 4
é uma matriz 2 × 2
~1~

2. 4.
 9 
0
 
1
E= 3
 
0
9
 
0
 
é uma matriz 6 × 1
MATRIZ QUADRADA
É aquela em que o número de linhas é igual ao de colunas.
Exemplos:
1.
A =  8
matriz quadrada de ordem 1
2.
2

 0 7
B=


 9 1 
matriz quadrada de ordem 2
3.



C= 




0
1
8
3
8
3
7
5
3 


9 


2 

matriz quadrada de ordem 3
MATRIZ LINHA
É aquela que possui somente uma linha.
Exemplos:
1.
A=
0
3
1
2.
2
B= 
5
1

3

7
matriz linha do tipo 1 × 4
matriz linha de ordem 1 × 3
MATRIZ COLUNA
É aquela que possui somente uma coluna.
Exemplos:
1.
0 
A = 1 
 
8 
 
2.
 1
9
 
B= 3
 
7
 
0
~2~

3. EXERCÍCIOS
1) Dê o tipo de cada uma das matrizes:
 7 1 0 
Modelo: A =  2 5 10 


 1 3 6  3 × 3


 8 5 2 3 
B =  1 0 9 1 
a)


 3 6 9 12 


b)
D =  1 2
c)
5 
E=  
9 
1 
2
F=  
3
 
4
d)
e)
C =  5 6 7 8
2) No exercício anterior:
a)
b)
c)
Quais são as matrizes quadradas?
Quais são as matrizes linhas?
Quais são as matrizes colunas?
Notação genérica:
Representamos genericamente uma matriz do tipo m x n escolhendo uma letra minúscula com dois índices
para representar cada um dos seus elementos, de modo que o primeiro índice indique a linha a que o elemento
pertence e o segundo índice, a coluna.
Exemplo:
 a11
a
 21
A =  a 31


 a m1

a12
a 22
a 32
a m2
a1n 
a 2n 

a 3n 


a mn 

a13
a 23
a 33
a m3
Assim:
a11 (a um um) é um elemento da 1ª linha e 1ª coluna.
a 32 (a três dois) é um elemento da 3ª linha e 2ª coluna.
a 23 (a dois três) é um elemento da 2ª linha e 3ª coluna.
Abreviadamente, podemos representar essa matriz A tomando-se um elemento genérico a ij , onde 1  i  m e
1 j  n :
A   a ij 
m×n
Exemplo:
 
Construa a matriz A  a ij do tipo 2 × 3 , sendo a ij  i + j .
a11  1 + 1  2
a12  1 + 2  3
a 21  2 + 1  3
a 22  2 + 2  4
a13  1 + 3  4
2 3 4
Logo: A = 

3 4 5
a 23  2 + 3  5
~3~

4. EXERCÍCIOS
3) Dada a matriz:
 7 1 0 
A =  2 5 10 


 1 3 6 


a)
b)
Qual é a sua ordem?
Dê o valor dos seguintes elementos: a11 , a 21 , a 33 , a12 , a 31 .
4) Construa a matriz
A   a ij  do tipo 2 × 3 , sendo a ij  2i + j .
5) Construa a matriz
B   bij 
3×1
, sendo bij  3i  j .
6) Construa a matriz quadrada de ordem 3,
C   cij  , sendo cij  i 2 + j2 .
DIAGONAL PRINCIPAL E DIAGONAL SECUNDÁRIA
Na matriz quadrada de ordem n abaixo:
 a11
a
 21
A =  a 31


 a m1

a12
a 22
a 32
a m2
a1n 
a 2n 

a 3n  ,


a mn 

a13
a 23
a 33
a m3
o conjunto D= a11 , a 22 , a 33 , a 44 , a 55 ,
diagonal secundária.
, a nn  (elementos de índices iguais) chama-se diagonal principal e a outra
Exemplos:
1.


7
B

8


diagonal
secundária
3
2






diagonal
principal
2.


4

C
0

5



diagonal
secundária
6 8
7 9
1 9








diagonal
principal
IGUALDADE DE MATRIZES
Duas matrizes são iguais se e somente se são do mesmo tipo e cada elemento da primeira matriz é igual ao correspondente da segunda.
Exemplos:
1.
1 4 
5 9 


=
 1

 3  2 
 5  1 

32 
~4~

5. 2.
Dadas as matrizes:
x + 1
A
 2
5 
3
 e B2
3y 

5
,
12 

Para quais valores de x e y A e B são iguais?
x + 1
 2

5  3

3y   2
 
5  x + 1 = 3  x = 2

12  3y = 12
 y=4

EXERCÍCIOS
7) Calcule os valores de
a)
b)
c)
x e y nas seguintes igualdades:
x  3  1 4 
 1


 6
9   6 y2 


x+6
 2 3x 8   2
 4 10 0    4
10

 
 8  3y  2
 2


x  5  11 

8 
3y  12

MATRIZ NULA
Uma matriz é nula quando todos os seus elementos são iguais a zero.
Exemplo:
0 0 0 
0 0 0 


MATRIZ TRANSPOSTA
É aquela que se obtém trocando ordenadamente suas linhas por colunas ou vice-versa.
A transposta de matriz A por exemplo, é indicada por A t .
4
Sendo A =  1

8

5
4
0  , então A t = 

 5
7

1
0
8
7

.

EXERCÍCIOS
8) Escreva a matriz nula do tipo:
a)
2×1
b)
3×2
b)
 1 4 
B= 8
2


 5 9 


9) Escreva a matriz transposta de:
a)
 1 3 4 
A= 

 11 2 3
~5~

6. OPERAÇÕES COM MATRIZES
ADIÇÃO DE MATRIZES
Dadas duas matrizes A e B do mesmo tipo, chama-se C = A + B a matriz que se obtém adicionando os elementos
correspondentes das matrizes A e B.
Exemplos:
1.
Sendo:
7
 7 1 10 
 e B =  3 3 5 
0


 4+7
5 +  1
7 + 10   11 4 17 
Então A + B = 
.
 =
1 +  3
0 + 5   5 4 5 


 2+3
4
A= 
2
2.
5
1
Determine x
 4 x

+
 7 8 
4 + y = 10
e y tais que:
 y 10   10

=
 1 7   8
x + 10 = 8
y = 10  4
y= 6
8

1
x = 8  10
x = 2
EXERCÍCIOS
10) Sendo:
8 3


A =  2 4
1 5


1 4


B = 5 3
8 5


 1 8 


C =  2 4 
 3 5 


Calcule:
a)
b)
11) Calcule
a)
b)
c)
d)
A+B
A+C
B+C
A+B+C
x , y e z nas seguintes igualdades:
3 2
x

+
 7 y z 
 x 5   1

 
 y 1  +  3
 z
0   4

 
 1 4 1   2

=
 2 5 2   9
1   1 6 
 

2= 2 1
5   5 5 
 

7
0
1

2
MATRIZ OPOSTA
Chama-se oposta de uma matriz A, a matriz A que se obtém trocando o sinal de todos os elementos de A.
Exemplo:
3
A oposta de A = 
1
0 2 
é A =
4 5 

 3
 1

0
4
2
.
5

~6~

7. SUBTRAÇÃO DE MATRIZES
Dadas A e B do mesmo tipo, a matriz A  B é a matriz que se obtém adicionando a matriz A à matriz oposta de
B:
A  B = A +  B 
Exemplo:
A
B
 4 3
 1

  
 2 5
2
A +  B 
B
A
2   4 3   1 2   5
 =
 +
 =
7   2 5   2 7   0
1

2 
EXERCÍCIOS
12) Dadas as matrizes:
3 8


A = 2 1
 4 5


 1 0 


C =  3 7 
 4 2 


1 7


B=  3 4 
 4 5 


Calcule:
a)
b)
A  B
B  A
c)
d)
AC
A+B  C
MULTIPLICAÇÃO DE UMA MATRIZ POR UM NÚMERO REAL
 
Dada uma matriz A  a ij
B =  k  aij 
m×n
m×n
e um número real k , chamamos de produto do número k , pela matriz A, a matriz
, ou seja, para obter este produto basta multiplicar pelo número k cada elemento da matriz A.
Exemplos:
6   7  4
 
1=
  70
7 
1.
 4
7  
 0


2.
7   6  
  28
1 =
7   0
7 
Dadas as matrizes:
 3
A= 
0
4
7
1

8
8
B= 
0
1
9
42 

1 
3

5
Calcule 3A + 2B .

3




3
0
9
0
4
7
12
21
 8 1 3 
 2

0 9 5
3 
 16 2 6   25
  
=
24 
 0 18 10   0
1

8
14
39
9 

34 
~7~

8. EXERCÍCIOS
13) Calcule:
a)
 1

4
3  
 2

 1
2
5
0
8






 3
2  
 4
b)
5

0
c)
1 
8
4 
14) Dadas as matrizes:
2
A= 
4
3 

1 
 2 8 
C= 

 1 3 
0 1
B= 

 2 3
Calcule:
a)
b)
5A + 3B
6A  3B
c)
d)
A + 5B  2C
2B  C
MULTIPLICAÇÃO DE MATRIZES
Vimos que a adição de matrizes só é possível quando as matrizes são do mesmo tipo. A multiplicação de matrizes
exige que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz.
 
Dadas as matrizes A  a ij
m×n
e B   b jk 
n×p
, define-se produto AB =  cik  do tipo m x p tal que o elemento
cik é obtido multiplicando-se ordenadamente os elementos da linha i de A pelos elementos da coluna k de B e somando-se os produtos obtidos.
Exemplos:
1.
3 1


Sejam A =  2 5  e B =
4 7


 2 5


4 7
Sendo L1 , L 2 , L3 linhas de A e C1 , C 2 colunas de B,
 L1C1

A  B  L 2C1
L C
 3 1
L1C2 

L 2C2  .
L 3C 2 

3  2 + 1  4 3  5 + 1  7


A  B  2  2 + 5  4 2  5 + 5  7
 4  2 + 7  4 4  5 + 7  7


2.
 10 22 


A  B  24 45  .
 36 69 


3 4 8
7  
=
9 5 2
 1  3 + 7  9 1  4 + 7  5 1  8 + 7  2 =  66 39 22 
1
~8~

9. EXERCÍCIOS
15) Calcule os produtos indicados:
a)
b)
c)
d)
2
1
5   
 4
e)
 2
 1 3 4    1 
 
5
 
 5 3  1 4

  

 0 3   2 5 
 1 2   3 8 3 

  

 3 4   1 2 4 
f)
g)
h)
3   1
  
3   3
4
2 3 1 

  2
4 0 1  1

2

0
 5 3  1

  
8 9 0
1 0  2

  
0 1 7
3
2
4
1
5

4
1

3 
5

0

1
3

0
MATRIZ IDENTIDADE
A matriz quadrada de ordem n onde todos os elementos da diagonal principal são iguais a 1 e os outros elementos são iguais a zero, chama-se matriz identidade.
Exemplos:
1.
1 0
I2 = 

0 1
2.
1 0 0


I3 =  0 1 0 
0 0 1


MATRIZ INVERSA
Uma matriz quadrada de ordem n é inversível se existir uma matriz B tal que A  B = In e B  A = I n . Indica-se a
matriz B por A -1 .
Se não existir a inversa de A, então A não é inversível.
Exemplo:


1
2 
6 
.
 é
3  7
5 


 3


 7
 
2  15  1 + 6     15   2  + 6  5 
 3
 = 1
=

 0
7
5   7  1 + 3   
7   2  + 3  5  

 3
 





1  15 +  2   7 1  6 +  2   3   1
6
=
=
3  7
7
0
  6+5  3  
   15 + 5  7

3
 3



2 
 1
.
é a inversa de 
 7 5 


 3

15
Mostre que a matriz inversa de A = 
7
15

7

 1

 7

 3

1
6 
  
3  7

 3

2 
15
  
7
5  


15
Portanto, 
7
6

3
0

1
0

1
~9~

10. EXERCÍCIOS
16) Mostrar que as duplas de matrizes abaixo são inversas:
a)
b)
 7 4   3 4 


 e
 5 3   5 7 
c)
 5 8   3 8 


 e
 2 3   2 5 
d)
7

1  
8 7 
2


 e
 2 2   1 4 




 3 7   12 7 

 e

 5 12   5 3 
~ 10 ~

11. Gabarito
1)
a) 3 × 4
b) 1 × 4
c) 1 × 2
d) 2 × 1
e) 4 × 1
2)
a) A
b) C e D
c) E e F
3)
a) 3 × 3
b) a11 = 7 , a 21 = 2 , a 33 =  6 , a12 =  1 , a 31 =  1
4)
3 4 5
5 6 7 


6)
2
5
 
8 
 
 2 5 10 
 5 8 13


10 13 18


7)
a)
x=7
y = ±3
5)
b)
0
a)  
0
9)
 1 11 
a)  3 2 


 4 3


9
10) a)  7

9

7
b)  0

 2

7
7

10 

11 
0

0

 10
 26

 12
b) 
 18
14) a)


 b)  6
 8




x=3
y=4
c)
x = ±4
y=2
1
b) 
 4
0
c)  3

5

8
d)  5

6

8
2
12 
1

0

15
3

5

 11
c) 
 6
5
9 


 8
35 
15

4
 11 0 5 2 
e) 

 9 6 3 12 
15 2 14 
f) 

17 9 1
5 3
g) 

8 9 
2
h)  7

8

3 5
0 4

1 6 

4   3 4   7  3+4   5 7   4  +4  7   1 0 
=
 


3   5 7   5  3+3   5 5   4  +3  7   0 1 


 3 4   7 4   3  7+  4   5 3  4+  4   3   1 0 
=






 5 7   5 3    5  7+7  5  5  4+7  3   0 1 
b)
 5 8   3 8   5   3 +8  2 5  8+8   5   1 0 
=

 




 2 3   2 5   2   3 +3  2 2  8+3   5    0 1 
 3 8   5 8    3  5+8  2  3  8+8  3   1 0 
 =

 




 2 5   2 3   2  5+  5  2 2  8+  5   3   0 1 
c)
x = 1, y =  5 , z = 4
b) x = 0 , y = 5 , z =  1
4 8
c)  5 8 


8 7 


 5 15 
d)  8 12 


4 2


c)
 6 14 
c) 
20 
 12

 2 6 
d) 

3 9
 1 4 5 
d) 

 5 16 7 
16) a)  7

5
10 
0 

12 
4 

21
15

19
b)
11) a)
2 1
12) a)  1 3


 8 10 


 2 1 
b)  1
3 


 8 10 


6
15
0
24
15) a)  22
0 0 
b) 0 0 


0 0 


8)
 3
 12
13) a) 
 6

 3

1
8 7 


 2 2   1



 1

 1


d)
3

5
7 
   8 1+7   1
2

4   2 1+2   1

 

 7
8     +7  4 
 2
=1 0
 0 1
7


2     +2  4  
 2


 7
 7 
7
 
 1  8+     2 1  7+     2 
 2
 2   1 0
2 8 7  
=


 0 1
  2 2 


4 
  1  8+4  2  1  7+4  2 



7   12 7   3 12+7   5
 

12   5 3   5 12+12   5

3   7  +7  3   1 0 
=

5   7  +12  3   0 1 

7   12  3+  7   5

12    5  3+3  5

12  7+  7  12   1 0 
=
 5  7+3 12   0 1 

 
 12 7   3


 5 3   5
~ 11 ~