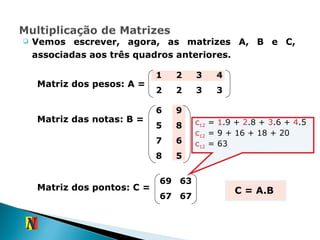
O documento apresenta informações sobre matrizes, incluindo sua definição, tipos, operações e exemplos. Resume os principais conceitos de matrizes como tabelas com linhas e colunas para organizar dados, indicando elementos individuais e realizando operações como soma, subtração e multiplicação.

2. O colégio Tales distribui, durante o ano letivo, 100 pontos por matéria. O quadro a seguir mostra os totais de pontos obtidos por Ana, Carlos e Pedro, em Matemática nos anos de 2006 e 2007. Quadros como esses ajudam a organizar dados. Fica mais fácil analisá-los, combiná-los com outros. Ana Carlos Pedro 2006 80 75 72,5 2007 76 82,5 78

3. Foi o matemático inglês, James Joseph, Sylvester, quem usou pela primeira vez esta forma de trabalhar com um conjunto de informações, dispondo-as em linhas e colunas em uma tabela. A um quadro desse tipo, damos o nome de Matriz . Cada número que o constitui é um elemento da matriz. O quadro apresentado é uma matriz 2 x 3 , isto é, possui 2 linhas e 3 colunas.

4. Para nomear matrizes, usamos letras latinas maiúsculas . Seus elementos ficam dentro de parênteses ou colchetes. Exemplo ou A = 80 75 72,5 76 82,5 78 80 75 72,5 76 85,2 78 A =

5. Nossa matriz tem 2 linhas e 3 colunas . Dizemos que ela é do tipo 2 x 3 (dois por três) ou, simplesmente, uma matriz 2 x 3. A = -> 1ª linha -> 2 ª linha 1ª coluna 2ª coluna 3ª coluna Nossa matriz é indicada por A 2x3 . 80 75 72,5 76 82,5 78

6. De maneira geral, indicamos um elemento de uma matriz por uma letra minúscula , acompanhada de dois índices, que definem sua posição na matriz. Um elemento genérico da matriz A é indicado assim: a ij i indica a linha do elemento j indica a coluna do elemento

7. Na matriz A exemplificada, temos a 11 = 80 a 12 = 75 a 13 = 72,5 a 21 = 76 a 22 = 82,5 a 23 = 78 80 75 72,5 76 82,5 78 A =

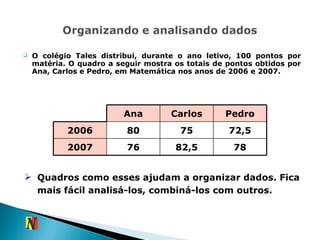
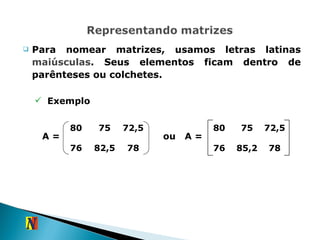
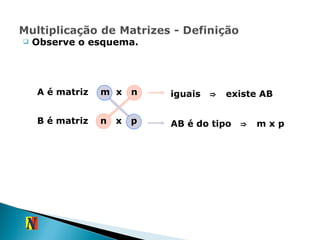
8. Se m e n são dois números naturais positivos, chama-se matriz do tipo m x n todo quadro formado por m.n números reais, dispostos de forma ordenada em m linhas e n colunas . Uma matriz genérica A m x n pode ser representada assim: a mn ... a m3 a m2 a m1 ... a 23 a 13 ... ... ... ... ... ... a 2n a 22 a 21 a 1n a 12 a 11 A = De forma simplificada, temos A = [a ij ] m x n

9. Na matriz A representada a seguir, cada elemento a ij indica a média, em Matemática, da turma i no bimestre j. Identificar o tipo de matriz e obter a média da turma 2 no 3.º bimestre e a média da turma 3 no 4.º bimestre. A = A 3 x 2 . a 23 = 8,7 a 34 = 7 6,2 8,3 9 7,4 8 7,3 8,7 6,5 7,2 8,1 6,9 7

11. Uma matriz pode ser definida, indicando-se seu tipo e uma fórmula para o cálculo de cada elemento a ij , em função de i e j.

12. Construir a matriz A = (a ij ) 3x2 , em que a ij = 3i – j. a 32 a 31 a 22 a 21 a 12 a 11 A = a ij = 3 i – j a 11 = 3. 1 – 1 = 2 a 12 = 3. 1 – 2 = 1 a 21 = 3. 2 – 1 = 5 a 22 = 3. 2 – 2 = 4 a 31 = 3. 3 – 1 = 8 a 32 = 3. 3 – 2 = 7 A = 2 1 5 4 8 7

13. Construir a matriz B = (b ij ) 2x2 , tal que b 22 b 21 b 12 b 11 B = b 11 = 2. 1 + 1 = 3 b 12 = 2 1 = 2 b 21 = 2. 2 + 1 = 5 b 22 = 2. 2 + 2 = 6 B = b ij = 2i + j, se i ≥ j j i , se i < j 3 2 5 6

14. Uma matriz que tem os seus elementos iguais a zero é chamada matriz nula. Existe uma matriz nula de cada tipo. A matriz nula pode ser indicada por O m x n . É uma matriz nula 2 x 3. O = O = É uma matriz nula 2 x 2. 0 0 0 0 0 0 0 0 0 0

15. Uma matriz que tem apenas uma linha é chamada de matriz linha . Uma matriz que tem somente uma coluna é denominada de matriz coluna . Exemplos É uma matriz linha 1 x 3. É uma matriz coluna 2 x 1. – 1 2 5 3 6

17. Chama-se matriz quadrada toda matriz em que o número de linhas é igual ao de colunas. O número de linhas (ou colunas) é a ordem da matriz. é matriz quadrada de ordem 2. é matriz quadrada de ordem 3. 0 3 – 2 5 3 0 – 3 7 2 – 5 1 4 0

18. Numa matriz quadrada A =[a ij ], de ordem n, chama-se Diagonal principal o conjunto dos elementos a ij em que i = j ; Diagonal secundária o conjunto dos elementos a ij em que i + j = n + 1 ; Diagonal secundária (i + j = 4) Diagonal principal (i = j) a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

19. Dizemos que duas matrizes A e B são iguais só se elas são do mesmo tipo e cada elemento de uma delas é igual ao elemento de mesma posição da outra. Se alguma das condições anteriores falhar, dizemos que A e B são matrizes diferentes.

20. Verificar se as matrizes A e B abaixo são iguais. A = B = As matrizes são do mesmo tipo (3 x 2) e têm os mesmos elementos. Elas são diferentes pois os elementos 5 e 8 ocupam posições diferentes. 2 1 5 4 8 7 2 1 8 4 5 7

21. Calcular x, y, z e t para que ocorra a igualdade. = 2 x = 4 y + 1 = 5 x + z = –1 t – y = 3 ⇒ 2 x = 2 2 ⇒ x = 2 ⇒ y = 4 ⇒ 2 + z = –1 ⇒ z = –3 ⇒ t – 4 = 3 ⇒ t = 7 2 x – 1 y + 1 3 4 x + z 5 t – y

22. Encontre os valores de x e y, para que a matriz M abaixo seja nula. M = x 2 – 1 = 0 x 2 – x – 2 = 0 x 2 – y 2 = 0 x + y = 0 ⇒ x = ± 1 ⇒ x = –1 ou x = 2 ⇒ x = –1 e y = 1 ⇒ x = –y x 2 – 1 x 2 – x – 2 x 2 – y 2 x + y

24. Em certos casos surge a necessidade de efetuar operações com matrizes. Adição; Subtração; Multiplicação de uma constante real por uma matriz; Multiplicação.

25. Sendo A e B matrizes de mesmo tipo e k uma constante real, definem-se as seguintes operações: Adição de matrizes : A + B é a matriz em que cada elemento é a soma dos elementos de mesma posição em A e B. Subtração de matrizes : A – B = A + (–B) , é a soma de A com a oposta de B. Multiplicação de um número por uma matriz : kA é a matriz obtida multiplicando-se, por k , cada um dos elementos de A .

26. Calcule: + = N = 3N = = 2 – 1 1 3 4 5 – 5 – 2 2 + 4 – 1 + 5 1 – 5 3 – 2 3 -7 10 -1 8 -5 0 4 -2 9 -21 30 -3 24 -15 0 12 6 6 4 – 4 1

28. Veja como podemos apresentar os dados referente à tabela da introdução de matrizes. A = B = ⇒ Ana Carlos Pedro 2006 80 75 72,5 2007 76 82,5 78 2006 2007 Ana 80 76 Carlos 75 82,5 Pedro 72,5 78 80 75 72,5 76 82,5 78 78 72,5 82,5 75 76 80

29. Se A é uma matriz do tipo m x n , chama-se transposta de A (simbolicamente A t ), a matriz do tipo n x m , obtida de A, trocando-se de posição linhas com colunas, de forma que A = (a ij ) m x n ⇒ A t = (a ji ) n x m A = – 5 1 0 – 1 3 2 A t = ⇒ 2 – 1 1 3 0 – 5

30. Chama-se oposta de uma matriz A a matriz representada por –A , cujos elementos são os opostos dos elementos de mesma posição em A. A oposta da matriz A = , é a matriz – A = 0 3 – 2 5 0 – 3 2 – 5

31. Chama-se matriz identidade de ordem n a matriz quadrada indicada I n tal que. Os elementos da diagonal principal são todos iguais a 1; Todos os outros elementos são iguais a 0; é matriz identidade de ordem 2. é matriz identidade de ordem 3. I 2 = I 3 = 1 0 0 1 1 0 0 0 1 0 0 0 1

32. Toda matriz quadrada em que todos os elementos fora da diagonal principal são iguais a zero é chamada matriz diagonal. Chama-se traço de uma matriz quadrada a soma dos elementos de sua diagonal principal . M = N = Traço de M é –2. Traço de N é 3/2. 3 0 0 – 5 ½ 0 0 0 0 0 0 0 2

33. Calcule o traço da matriz quadrada A abaixo, sabendo que ela é matriz diagonal. A = x + 2y = 0 x – y + 6 = 0 ⇒ x = –4 ⇒ x + 2y = 0 2x – 2y + 12 = 0 x (2) + 3x + 12 = 0 e y = 2 O traço da matriz é: x – 2y + x + y = 2x – y = –10 x – 2y x – y + 6 x + 2y x + y

34. Toda matriz quadrada que é igual a sua transposta é chamada matriz simétrica. N = A é simétrica ⇔ A = A t Exemplo 1 – 3 5 – 3 2 – 1 5 – 1 6

35. Obtenha m, n, e p, para que seja simétrica a matriz. P = m + n = –1 m – 2n = 2 ⇒ m + n = –1 m – 2n = 2 p + 2 = 5 ⇒ 2m + 2n = –2 m – 2n = 2 + 3m = 0 ⇒ m = 0 e n = –1 ⇒ p = 3 3 m + n 2 – 1 1 5 m – 2n p + 2 0

36. Toda matriz quadrada que é igual à oposta de sua transposta é chamada matriz anti-simétrica. N = A é anti-simétrica ⇔ A = –A t Exemplo 0 3 – 5 – 3 0 – 1 5 1 0

37. Complete a matriz para que ela seja anti-simétrica. Q = 0 0 0 2 – 5 – 3 .... .... 5 – 2 .... 3 .... .... ....

38. Toda matriz quadrada na qual são nulos todos os elementos situados num mesmo lado da diagonal principal. A = B = Exemplos 3 1 0 – 5 ½ 7 3 0 – 2 1 0 0 2

39. Uma empresa fabrica dois produtos A e B , que podem ser acondicionados nas embalagens E 1 , E 2 e E 3 , com 12 , 24 ou 30 unidades, respectivamente. Os quadros abaixo mostram os custos de fabricação do produto e da embalagem, em cada caso. Custo do produto (R$) Custo da embalagem (R$) A B E 1 2 3 E 2 3 4 E 3 4 6 A B E 1 60 80 E 2 100 130 E 3 120 160

40. O fabricante quer vender o produto com lucro de 50% sobre o custo do produto, mas não quer obter lucro no custo da embalagem. Qual será o preço de venda dos produtos A e B . P = E = O preço de venda é obtido efetuando-se a operação: 1,5 . P + E 60 80 100 130 120 160 2 3 3 4 4 6

41. V = 1,5 . P + E P = E = 1,5 . P = 1,5 .160 1,5 .120 1,5 .100 1,5 .60 1,5 .130 1,5 .80 = 240 180 150 90 195 120 1,5 . P + E = + = 246 184 153 92 199 123 60 80 100 130 120 160 2 3 3 4 4 6 90 120 150 195 180 240 2 3 3 4 4 6

42. Veja como seriam os preços de venda dos dois produtos nas três possíveis embalagens. Preço de venda (R$) A B E 1 92 123 E 2 153 199 E 3 184 246

43. Dada as matrizes abaixo obter a matriz 3M – 2N + I 2 . N = M = 3.M = 3 .2 3 .3 3 .1 3 .–2 = – 2.M = – 2 .4 – 2 .3 – 2 .0 – 2 .2 = – 2 1 3 2 2 0 3 4 – 6 3 9 6 – 4 0 – 6 – 8

44. Dada as matrizes abaixo obter a matriz 3M – 2N + I 2 . N = M = 3M –2N + I 2 = 3.M + (–2.N) + I 2 = – 1 3 3 – 9 = + + = – 2 1 3 2 2 0 3 4 – 6 3 9 6 – 4 0 – 6 – 8 1 0 0 1

46. Resolver a equação 3X – A = 2B, onde B = A = A matriz X deve ser do mesmo tipo de A e B. X = 3.X – A = 2B ⇒ 3. – = 2. – 5 0 – 1 4 1 – 3 2 1 x y z t x y z t – 5 0 – 1 4 1 – 3 2 1

47. 3.X – A = 2B ⇒ + = ⇒ 3t – 4 3z + 1 3y 3x + 5 = 3x + 5 = 2 3y = –6 3z + 1 = 4 3t – 4 = 2 ⇒ x = –1 y = –2 z = 1 t = 2 ⇒ X = 3x 3y 3z 3t 5 0 1 – 4 2 – 6 4 2 2 – 6 4 2 – 1 – 2 1 2

48. Resolver a equação 3X – A = 2B, onde B = A = Equações como essa podem ser resolvidas, também, como se fossem equações algébricas . Veja . 3.X – A = 2B ⇒ 3.X = A + 2B ⇒ X = 1 3 A + 2B = + = 6 3 – 6 – 3 (A + 2B) – 5 0 – 1 4 1 – 3 2 1 – 5 0 – 1 4 2 – 6 4 2

49. Resolver a equação 3X – A = 2B, onde B = A = Equações como essa podem ser resolvidas, também, como se fossem equações algébricas . Veja . 3.X – A = 2B ⇒ 3.X = A + 2B ⇒ X = (A + 2B) 1 3 X = = 1 3 2 1 – 2 – 1 – 5 0 – 1 4 1 – 3 2 1 – 3 – 6 3 6

51. Suponha que A, B e C sejam matrizes de mesmo tipo e que O seja a matriz nula de mesmo tipo daquelas. Valem, para a adição, as seguintes propriedades: Associativa : (A + B) + C = A + (B + C) Comutativa : A + B = B + A Existência do elemento neutro , a matriz O, tal que A + O = O + A = A Existência do elemento oposto de A, a matriz –A tal que A + (–A) = O. (A + B) t = A t + B t

53. O colégio Tales e o colégio Platão distribuem em cada bimestre letivo, um total de 10 pontos por matéria. No entanto, os pesos em cada bimestre diferem nos dois colégios. Veja o quadro a seguir Peso por bimestre em cada colégio 1º B 2º B 3º B 4º B Tales 1 2 3 4 Platão 2 2 3 3

54. Dois alunos das duas escolas, que eram amigos, resolveram comparar a soma dos pontos obtidos em Matemática no seu colégio com a que teriam obtido, caso estudasse no outro colégio. Nota de cada aluno por bimestre André Pedro 1º B 6 9 2º B 5 8 3º B 7 6 4º B 8 5

55. Veja o total de pontos que cada um teria feito, estudando no colégio Tales . André: 1 .6 + 2 .5 + 3 .7 + 4 .8 = 6 + 10 + 21 + 32 = 69 Pedro: 1 .9 + 2 .8 + 3 .6 + 4 .5 = 9 + 16 + 18 + 20 = 63 André Pedro 1º B 6 9 2º B 5 8 3º B 7 6 4º B 8 5 1º B 2º B 3º B 4º B Tales 1 2 3 4 Platão 2 2 3 3

56. Veja o total de pontos que cada um teria feito, estudando no colégio Platão . André: 2 .6 + 2 .5 + 3 .7 + 3 .8 = 12 + 10 + 21 + 24 = 67 Pedro: 2 .9 + 2 .8 + 3 .6 + 3 .5 = 18 + 16 + 18 + 15 = 67 André Pedro 1º B 6 9 2º B 5 8 3º B 7 6 4º B 8 5 1º B 2º B 3º B 4º B Tales 1 2 3 4 Platão 2 2 3 3

57. O quadro a seguir sintetiza os resultados. Pontos de cada aluno por colégio André Pedro Tales 69 63 Platão 67 67

58. Vemos escrever, agora, as matrizes A, B e C, associadas aos três quadros anteriores. Matriz dos pesos: A = Matriz das notas: B = Matriz dos pontos: C = c 12 = 1 .9 + 2 .8 + 3 .6 + 4 .5 c 12 = 9 + 16 + 18 + 20 c 12 = 63 C = A.B 1 2 3 4 2 2 3 3 6 9 5 8 7 6 8 5 69 63 67 67

59. Sob certas condições, definem-se a multiplicação de matrizes. Dadas duas matrizes A e B Existe o produto AB (ou A.B ) se, e somente se, o número de colunas de A (1ª matriz) é igual ao número de linhas de B (2ª matriz); Existindo a matriz AB, ela tem o número de linhas de A (1ª matriz) e o número de colunas de B (2ª matriz).

60. Observe o esquema. A é matriz m x n B é matriz n x p iguais ⇒ existe AB AB é do tipo ⇒ m x p

61. Dado as matrizes A e B abaixo, mostrar que é definido e obter o produto AB. B = A = A é matriz 2 x 3 B é matriz 3 x 2 iguais ⇒ existe AB AB é do tipo ⇒ 2 x 2 AB = – 3 1 0 2 4 – 2 – 1 2 3 5 – 2 6 x 11 x 12 x 21 x 22

62. Dado as matrizes A e B abaixo, mostrar que é definido e obter o produto AB. B = A = Cálculo de x 11 : x 11 = –3 .(–1) + 1 .3 + 0 .(–2) = 3 + 3 + 0 = 6 Cálculo de x 12 : x 12 = –3 .2 + 1 .5 + 0 .6 = –6 + 5 + 0 = –1 – 3 1 0 2 4 – 2 – 1 2 3 5 – 2 6

63. Dado as matrizes A e B abaixo, mostrar que é definido e obter o produto AB. B = A = Cálculo de x 21 : x 21 = 2.(–1) + 4.3 + (–2).(–2) = –2 + 12 + 4 = 14 Cálculo de x 22 : x 22 = 2.2 + 4.5 + –2 .6 = 4 + 20 – 12 = 12 – 3 1 0 2 4 – 2 – 1 2 3 5 – 2 6

64. Dado as matrizes A e B abaixo, mostrar que é definido e obter o produto AB. B = A = Conclusão: AB = = – 3 1 0 2 4 – 2 – 1 2 3 5 – 2 6 x 11 x 12 x 21 x 22 6 – 1 14 12

65. Observe que no caso das matrizes A 2x3 e B 3x2 do exemplo anterior, existe o produto BA que é do tipo 3 x 3. Ainda que, em certos casos, tanto AB como BA sejam definidos, em geral AB ≠ BA . Se existirem tanto AB quanto BA e, além disso, AB = BA , dizemos que A e B comutam . Se A é uma matriz quadrada, existe o produto AA, que também pode ser indicado por A 2 .

67. Suponha que A, B e C sejam matrizes de mesmo tipo e que O seja a matriz nula de mesmo tipo daquelas. Valem, para a multiplicação, as seguintes propriedades: Associativa : (AB)C = A(BC) Distributiva : A(B + C) = AB +AC e (B + C)A = BA + CA Seja A m x n , A.I n = I m .A = A (AB) t = B t .A t

69. Dado as matrizes A e B abaixo, resolver a equação matricial AX = B. B = A = Vamos analisar primeiro de que tipo é a matriz X. A é matriz 2 x 2 X é matriz m x n existe AX ⇒ m = 2 AX é do tipo ⇒ 2 x n AX 2 x n = B 2 x 1 ⇒ n = 1 X = 2 – 1 1 1 5 4 x y

70. Dado as matrizes A e B abaixo, resolver a equação matricial AX = B. 2x – y = 5 x + y = 4 B = A = AX = B ⇒ . = x + y 2x – y 4 5 = ⇒ x = 3 y = 1 ⇒ X = 2 – 1 1 1 5 4 x y 2 – 1 1 1 5 4 3 1

72. Dadas as matrizes A e B abaixo, vamos obter os produtos AB e BA. AB = A = B = . = – 2 + 3 – 1 + 1 6 – 6 3 – 2 = 1 0 0 1 BA = . = – 2 + 3 3 – 3 – 2 + 2 3 – 2 = 1 0 0 1 Note que AB = BA = I 2 , matriz identidade de ordem 2. 1 1 2 3 3 – 1 – 2 1 1 1 2 3 3 – 1 – 2 1 3 – 1 – 2 1 1 1 2 3

73. AB = BA = I 2 , matriz identidade de ordem 2. Dizemos que: A é a inversa de B ( A = B –1 ); B é a inversa de A ( B = A –1 ).

74. Dizemos que uma matriz quadrada A, de ordem n, é invertível se, e somente se, existir uma matriz B tal que AB = BA = I n . No caso a matriz B é chamada de inversa de A e é representada por A –1 . Portanto AA –1 = A –1 A = I n

75. Mostrar que a matriz A abaixo é invertível e obter sua inversa. A = Caso exista, A –1 ela será de ordem 2. A –1 = AA –1 = I 2 ⇒ . = ⇒ b – 3d 2b – 5d a – 3c 2a – 5c = 2 – 5 1 – 3 a b c d 2 – 5 1 – 3 a b c d 1 0 0 1 1 0 0 1

76. Mostrar que a matriz A abaixo é invertível e obter sua inversa. A = Resolvendo os sistemas encontramos a = 3, b = –5, c = 1 e d = –2. Logo ⇒ 2a – 5c = 1 a – 3c = 0 e 2b – 5d = 0 b – 3d = 1 A –1 = = 2 – 5 1 – 3 a b c d 3 – 5 1 – 2