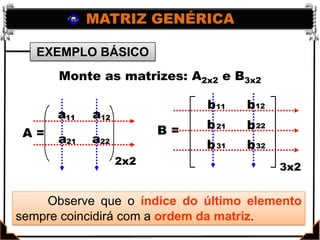
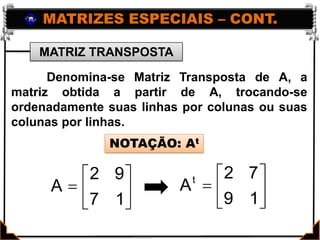
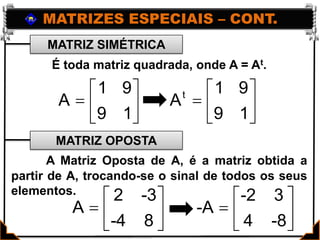
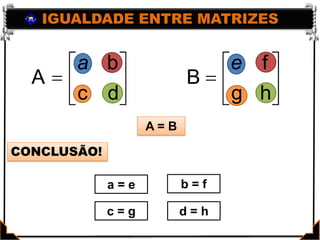
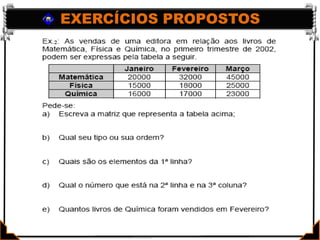
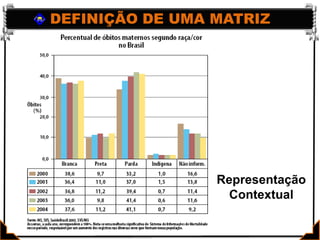
Este documento apresenta os conceitos básicos de matrizes, incluindo: (1) definição de matrizes e sua representação matemática; (2) tipos de matrizes como quadradas, retangulares, nulas e identidade; e (3) igualdade entre matrizes. Exemplos ilustram como localizar elementos e calcular a ordem de matrizes. Exercícios são fornecidos para praticar os conceitos.

1. TEORIA DAS MATRIZES AULA 01: Conceito, Igualdade e Tipos de Matrizes Professor MÁRIO PALHETA mspalheta@yahoo.com.br

2. DEFINIÇÃO DE UMA MATRIZ Representação Contextual

3. REPRESENTAÇÃO MATEMÁTICA ( ) ou [ ] ou || ||

4. ORDEM MATRICIAL 1ª linha 2ª linha 3ª linha 4ª linha 5ª linha 5 LINHAS E 5 COLUNAS 1ª coluna 3ª coluna 5ª coluna 2ª coluna 4ª coluna 5x5 (CINCO POR CINCO) ORDEM MATRICIAL: 5 LINHAS E 5 COLUNAS = 25 ELEMENTOS

5. LOCALIZAÇÃO DE UM ELEMENTO 2ª linha 4ª linha 1ª coluna 4ª coluna Elemento: 36,4 Posição: 2 1 (Dois Um) Elemento: 0,6 Posição: 4 4 (Quatro Quatro)

6. MATRIZ GENÉRICA EXEMPLO BÁSICO Monte as matrizes: A2x2 e B3x2 b b 12 11 a a 11 12 b b 22 21 B = A = a a 22 21 b b 31 32 2x2 3x2 Observe que o índice do últimoelemento sempre coincidirá com a ordem da matriz.

7. MATRIZES ESPECIAIS MATRIZ LINHA MATRIZ COLUNA É toda matriz do tipo 1 x n, ou seja, com uma única linha. ORDEM: 1 x 4 É toda matriz do tipo m x 1, ou seja, com uma única coluna. ORDEM: 3 x 1

8. MATRIZES ESPECIAIS – CONT. MATRIZ RETANGULAR MATRIZ QUADRADA É toda matriz do tipo m x n, ou seja, com o números de linhas diferente do de colunas. ORDEM: 1 x 4 É toda matriz do tipo m x m, ou seja, com o número de linhas igual ao número de colunas. Neste caso dizemos que a matriz é de ordem “m”. ORDEM: 2 x 2 Matriz de Segunda Ordem

9. MATRIZES ESPECIAIS – CONT. ATENÇÃO !!! Em toda Matriz Quadrada é possível localizarmos duas diagonais, chamadas de: DIAGONAL PRINCIPAL e DIAGONAL SECUNDÁRIA. Diagonal Secundária D.P.: 5 / 1 / 15 D.S.: 8 / 1 / 10 Diagonal Principal

10. O2 x 2= MATRIZES ESPECIAIS – CONT. MATRIZ NULA MATRIZ DIAGONAL É toda matriz onde seus elementos são iguais a zero. NOTAÇÃO: Om x n O2X2 = É toda matriz quadrada onde todos os elementos que não estão na diagonal principal são nulos.

11. MATRIZES ESPECIAIS – CONT. MATRIZ IDENTIDADE É toda matriz quadrada onde os elementos da diagonal principal são iguais a 1 e os demais são nulos. NOTAÇÃO: In

12. MATRIZES ESPECIAIS – CONT. MATRIZ TRANSPOSTA Denomina-se Matriz Transposta de A, a matriz obtida a partir de A, trocando-se ordenadamente suas linhas por colunas ou suas colunas por linhas. NOTAÇÃO: At

13. MATRIZES ESPECIAIS – CONT. MATRIZ SIMÉTRICA MATRIZ OPOSTA É toda matriz quadrada, onde A = At. A Matriz Oposta de A, é a matriz obtida a partir de A, trocando-se o sinal de todos os seus elementos.

14. IGUALDADE ENTRE MATRIZES A = B CONCLUSÃO! b = f a = e c = g d = h

15. EXEMPLO - APOSTILA Na igualdade abaixo, encontre o valor dos termos desconhecidos.

16. EXERCÍCIOS PROPOSTOS

17. EXERCÍCIOS PROPOSTOS

18. EXERCÍCIOS PROPOSTOS

19. EXERCÍCIOS PROPOSTOS