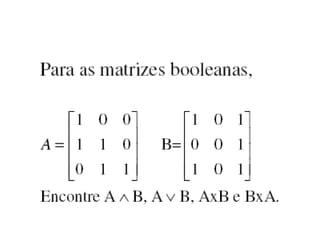
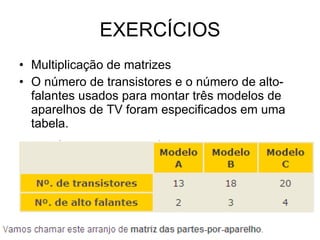
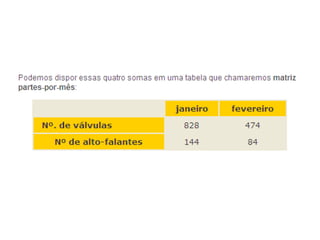
Este documento descreve as características básicas de matrizes, incluindo suas dimensões, elementos, transposição e operações como adição, subtração e multiplicação. Matrizes podem ser quadradas ou retangulares, e vetores são considerados matrizes de dimensão especial.

1. MATRIZES

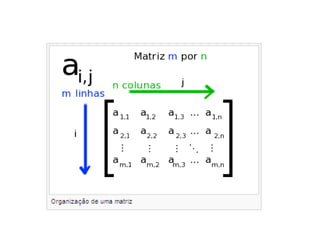
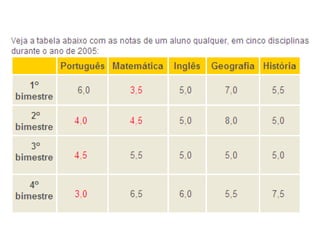
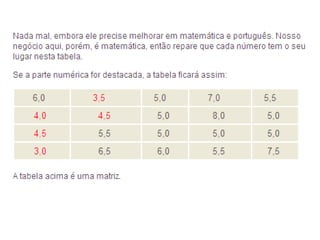
3. As linhas horizontais da matriz são chamadas de linhas e as linhas verticais são chamadas de colunas . Uma matriz com m linhas e n colunas é chamada de uma matriz m por n (escreve-se m×n ) e m e n são chamadas de suas dimensões , tipo ou ordem . Um elemento de uma matriz A que está na i-ésima linha e na j-ésima coluna é chamado de elemento i,j ou ( i,j )-ésimo elemento de A . Ele é escrito como A i,j ou A [ i,j ].

4. Uma matriz onde uma de suas dimensões é igual a 1 é geralmente chamada de vetor . Uma matriz 1 × n (uma linha e n colunas) é chamada de vetor linha ou matriz linha , e uma matriz m × 1 (uma coluna e m linhas) é chamada de vetor coluna ou matriz coluna .

5. A matriz a seguir é uma matriz de ordem 2×3 com elementos naturais Nesse exemplo, o elemento a 1 2 é 2, o número na primeira linha e segunda coluna do quadro.

12. A transposta de uma matriz A m × n é a matriz A t n × m em que , ou seja, todos os elementos da primeira linha, tornar-se-ão elementos da primeira coluna, todos os elementos da segunda linha, tornar-se-ão elementos da segunda coluna, todos os elementos da n linha, tornar-se-ão elementos da m coluna.

14. Uma matriz é dita quadrada se tem o mesmo número de linhas e colunas, ou seja, quando podemos dizer que, m tem a mesma quantidade de elementos que n . Numa matriz quadrada A de ordem n × n, chama-se de diagonal principal os elementos a ij onde i = j, para i de 1 a n.

17. Operações envolvendo Matrizes Multiplicação por um escalar A multiplicação é uma das operações mais simples que podem ser feitas com matrizes. Para multiplicar um número k qualquer por uma matriz n×m A, basta multiplicar cada entrada aij de A por k . Assim, a matriz resultante B será também n×m e bij = k .aij. Com isso, pode-se pensar também na noção de dividir uma matriz por um número: basta multiplicá-la pelo inverso desse número. Mas essa noção pode ser perigosa: enquanto a multiplicação entre um número e uma matriz pode ser dita " comutativa ", o mesmo não vale para a divisão, pois não se pode dividir um número por uma matriz.

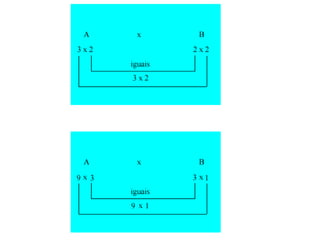
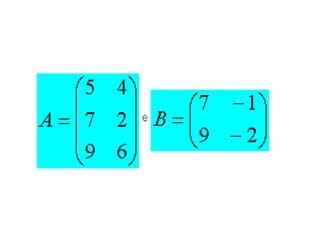
19. Adição e Subtração entre Matrizes Dado as matrizes A e B do tipo m por n , sua soma A + B é a matriz m por n computada adicionando os elementos correspondentes: ( A + B )[ i , j ] = A [ i, j ] + B [ i, j ].

24. Multiplicação de Matrizes Multiplicação de duas matrizes é bem definida apenas se o número de colunas da matriz da esquerda é o mesmo número de linhas da matriz da direita. Se A é uma matriz m por n e B é uma matriz n por p , então seu produto AB é a matriz m por p ( m linhas e p colunas) dada por:

31. Matrizes booleanas São matrizes que têm apenas elementos iguais a 0 ou 1. Podemos definir uma operação booleana de multiplicação A×B para matrizes booleanas usando multiplicação e soma booleanas, ao invés de multiplicação e adição usuais.

32. operações booleanas de multiplicação e adição

33. A multiplicação booleana de matrizes A X B é definida por:

36. EXERCÍCIOS Multiplicação de matrizes O número de transistores e o número de alto-falantes usados para montar três modelos de aparelhos de TV foram especificados em uma tabela.