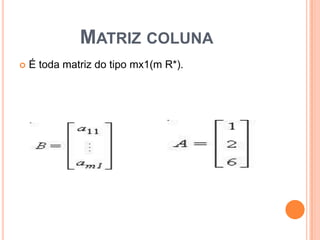
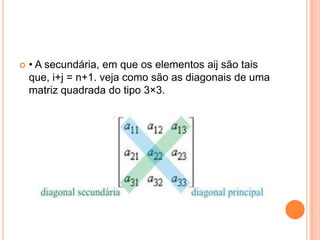
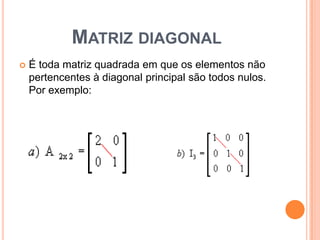
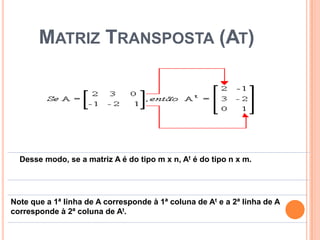
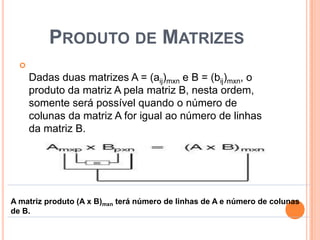
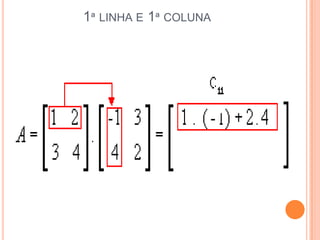
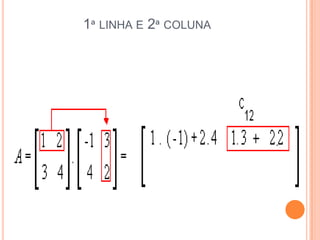
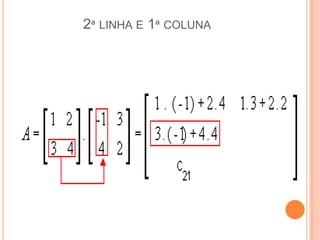
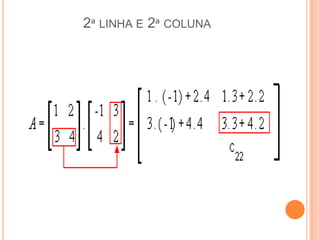
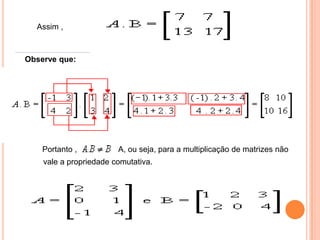
1) Uma matriz é uma tabela com linhas e colunas que representa elementos ordenados. 2) Existem diferentes tipos de matrizes como matrizes quadradas, diagonais, nulas e transpostas. 3) Podemos realizar operações com matrizes como soma, subtração e multiplicação seguindo regras de ordem das linhas e colunas.

1. Matriz

2. MatrizPodemos dizer que uma matriz é uma tabela com colunas (vertical) e linhas (horizontal). Então chamamos de matriz toda tabela m x n sendo que m e n podem assumir qualquer valor natural menos o zero. Sendo que m é o número de linhas e n o número de colunas. Para representar uma matriz devemos colocar as linhas e colunas entre parênteses, chaves ou entre duas barras duplas, veja alguns exemplos:

3. Observe que em cada matriz dos exemplos acima tem ao lado indicando o número de linhas e o de colunas da matriz, o primeiro exemplo esta indicado 2 x 3 que lê assim a matriz é de ordem dois por três. E cada número pertencente a uma matriz é o seu elemento. Se pegarmos uma matriz qualquer de ordem m x n, como iríamos representá-la? Cada elemento de uma matriz pertence a uma linha e uma coluna. Dada a matriz de ordem 3 x 2: O elemento - 5 pertence a 1ª linha e a 1ª coluna. O elemento 2 pertence a 2ª linha e 2ª coluna.

4. Para representarmos uma matriz de ordem 2 x 2 onde não temos seus elementos definidos, representamos da seguinte forma: a11 ; a21 ; a12 ; a22 são elementos da matriz de ordem 2 x 2 (duas linhas e duas colunas). Então o elemento a21 pertence a 2ª linha e 1º coluna.

5. Exemplo:Escreva a matriz A = (aA matriz A é de ordem 2 x 3, então podemos escrevê-la assim: i j)2 x 3 tal que ai j = 2i + j.

6. Agora os números que ocuparam o lugar de: a11, a21, a12, a22, a13 e a23, irão depender da equação dada no enunciado: ai j = 2i + j. Então iremos calcular cada elemento sabendo que: i é a linha que o elemento pertence. j é a coluna que o elemento pertence. a11 = 2 . 1 + 1 a21 = 2 . 2 + 1 a11 = 3 a21 = 5 a12 = 2 . 1 + 2 a22 = 2 . 2 + 2 a12 = 4 a22 = 6 a13 = 2 . 1 + 3 a23 = 2 . 2 + 3 a13= 5 a23 = 7

7. Então os elementos que pertencem a matriz A são:

8. Tipos de matrizesMatriz linhaÉ toda matriz do tipo 1xn(n ∈ R*).Observe os exemplos:

9. Matriz colunaÉ toda matriz do tipo mx1(m R*).

10. Matriz quadradaÉ Toda matriz quadrada possui duas diagonais:• A principal, composta por elementos aij tais que i=j, isto é:Toda matriz cujo numero de linhas é igual ao numero de colunas. Assim, chamamos matriz quadrada de ordem n toda matriz do tipo n x n. Exemplos:

11. • A secundária, em que os elementos aij são tais que, i+j = n+1. veja como são as diagonais de uma matriz quadrada do tipo 3×3.

12. Matriz nula: É toda matriz do tipo m x n cujos elementos são todos nulos. Para indicar uma matriz nula utiliza-s a notação:

13. Matriz diagonalÉ toda matriz quadrada em que os elementos não pertencentes à diagonal principal são todos nulos. Por exemplo:

14. Matriz Transposta (At)

15. Matriz Diagonal É uma matriz quadrada onde aij = 0, para i j, isto é, os elementos que não estão na diagonal principal são nulos.

16. Matriz simétricamatriz quadrada de ordem n tal que A = At . Por exemplo,

17. Matriz opostamatriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A.

18. Operações com Matrizes Igualdade de MatrizesDuas matrizes A = (aij)mxn e B = (bij)mxn de mesma ordem, são iguais se, e somente se, aij = bij.

19. Adição e subtração de MatrizesA soma de duas matrizes A = (aij)mxn e B = (bij)mxn de mesma ordem é uma matriz C = (aij)mxn tal que C = aij + bij. A subtração de matrizes é dada pela sentença:

20. ExemplosObservação: A + B existe se, e somente se, A e B forem do mesmo tipo

21. Produto de um Número Real por uma Matriz Se é um número real, o produto desse número por uma matriz A = (aij)mxn é uma matriz B = (bij)mxn tal que bij = . aij

22. Produto de MatrizesDadas duas matrizes A = (aij)mxn e B = (bij)mxn, o produto da matriz A pela matriz B, nesta ordem, somente será possível quando o número de colunas da matriz A for igual ao número de linhas da matriz B.

23. Os elementos da matriz produto são obtidos multiplicando-se cada elemento das linhas da matriz A pelo correspondente elemento das colunas da matriz B e adicionando os produtos obtidos. Vamos multiplicar a matriz para entender como se obtém cada Cij:

24. 1ª linha e 1ª coluna

25. 1ª linha e 2ª coluna

26. 2ª linha e 1ª coluna

27. 2ª linha e 2ª coluna

28. Assim , Portanto ,A, ou seja, para a multiplicação de matrizes nãovale a propriedade comutativa.

29. Vejamos outro exemplo com as matrizes