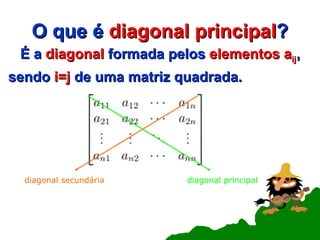
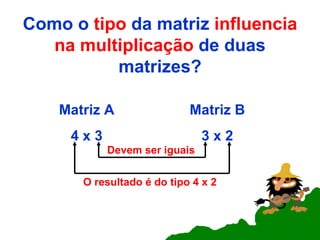
O documento aborda conceitos fundamentais sobre matrizes, incluindo definições e tipos como matrizes nula, linha, coluna, quadrada, diagonal, triangular, oposta, identidade e inversa. Além disso, discute operações como soma, subtração e multiplicação de matrizes, além de propriedades específicas, como simetria e traço. Exemplos práticos e exercícios são fornecidos para ilustrar os conceitos apresentados.

1. Matrizes

2. Ao final dessa aula você saberá: O que é matriz e suas representações. Igualdade de matrizes. A definição de: matriz nula, matriz linha, matriz coluna, matriz quadrada, matriz diagonal, matriz triangular, matriz oposta, matriz identidade e matriz inversa. O que é diagonal principal e diagonal secundária. Soma, subtração e multiplicação de matrizes.

3. O que é matriz ? É uma tabela de números que pode ser representada entre chaves ou entre colchetes . Exemplos: São matrizes com 2 linhas e 3 colunas. Então dizemos que é uma matriz 2 x 3.

4. Como é a representação genérica de uma matriz?

5. O que é índice de um elemento? É a representação da posição que o elemento ocupa dentro da matriz. Exemplo: O 3 é o elemento a 12 , ou seja, está na 1ª linha e na 2ª coluna .

6. Quando duas matrizes A e B são iguais ? Quando os elementos de mesmo índice são correspondentes . Exemplo:

7. Tente fazer sozinho! (PUC-MG)A matriz A = (a ij ) 2x3 é tal que: É correto afirmar que:

8. Solução a 11 = 2.1 – 3.1 = 2 – 3 = -1 a 12 = 3.1 + 2 = 3+ 2 = 5 a 13 = 3.1 + 3 = 3 + 3 = 6 a 21 = 3.2 + 1 = 6 + 1 = 7 a 22 = 2.2 – 3.2 = 4 – 6 = -2 a 23 = 3.2 + 3 = 6 + 3 = 9 Resposta: D

9. O que é matriz linha ? É uma matriz formada por apenas uma linha . Exemplo: É uma matriz formada por apenas uma coluna . Exemplo: O que é matriz coluna ?

10. O que é matriz nula ? É uma matriz que apresenta todos os elementos iguais a zero . Exemplos:

11. O que é matriz quadrada ? É a matriz que apresenta o mesmo número de linhas e colunas . Exemplos: Dizemos que a matriz A é de ordem 3 e que a matriz B é de ordem 2. Matriz 3 x 3 Matriz 2 x 2

12. O que é diagonal principal ? É a diagonal formada pelos elementos a ij , sendo i=j de uma matriz quadrada. diagonal principal diagonal secundária

13. Tente fazer sozinho! (Ufop-MG) Observe a matriz: Chama-se traço de uma matriz a soma dos elementos de sua diagonal principal. Determine x e y na matriz acima de tal forma que seu traço valha 9 e x seja o triplo de y.

14. Solução x = 3y 1 + 3y + y = 9  4y = 8  y = 2 x = 3.2  x = 6

15. O que é matriz diagonal ? É a matriz quadrada na qual todos os elementos que não pertencem a diagonal principal são iguais a zero . A diagonal principal deve apresentar pelo menos um elemento diferente de zero . Exemplos:

16. O que é matriz triangular ? É a matriz quadrada na qual os elementos abaixo ou acima da diagonal principal são iguais a zero . Exemplos:

17. O que é matriz oposta ? É a matriz cujos elementos são os opostos de uma matriz dada. Exemplos:

18. O que é matriz transposta ? É a matriz cujas colunas são iguais às linhas de uma matriz dada. Exemplo: Note que o número de linhas de A é o número de colunas de A t . O mesmo acontece com o número de colunas A é 3x2 e A t =2x3

19. Tente fazer sozinho! (UF-AM) Uma matriz quadrada é simétrica se, e somente se, A t = A. Se a matriz É simétrica, então o valor de é: a) – 1 b) 3 c) 1 d) 4 e) 0

20. Solução Resposta: letra c

21. O que é matriz identidade ? É a matriz quadrada que apresenta todos os elementos da diagonal principal iguais a 1 e os outros elementos iguais a zero . Exemplo:

22. Como somamos ou subtraímos matrizes? Basta somar ou subtrair os elementos correspondentes . As matrizes devem ser do mesmo tipo (m x n). Exemplos:

23. Como multiplicamos uma matriz por um número real ? Basta multiplicar todos os elementos da matriz por esse número real. Exemplo:

24. Como o tipo da matriz influencia na multiplicação de duas matrizes? Matriz A 4 x 3 Matriz B 3 x 2 Devem ser iguais O resultado é do tipo 4 x 2

25. Como efetuamos o produto de duas matrizes ? Dada uma matriz A = (a ij ) mxn e uma matriz B = (b ij ) nxp , o produto é uma matriz C = (c ij ) mxp , onde o elemento c ij é calculado multiplicando ordenadamente os elementos da linha i, da matriz A, pelos elementos da coluna j, da matriz B, e somando os produtos obtidos .

26. Exemplo 1 :

27. Exemplo 2 :

28. Tente fazer sozinho! 1) (Mackenzie-SP) Se o produto de matrizes é a matriz nula, x + y é igual a: a) 0 b) 1 c) -1 d) 2 e) -2

29. Solução

31. 2) (Fatec-SP) Seja a matriz , tal que . É verdade que a+b é igual a: a) 0 b) 1 c) 9 d) -1 e) -9

32. Solução Resposta: Letra B

33. O que é matriz inversa ? É matriz X de ordem n, cujo produto com a matriz A é igual a matriz identidade de ordem n . Ou seja, A.X = X.A = In, onde X = A -1 A matriz inversa de A É indicada por A -1 .

34. Exemplo: Logo, B = A -1

35. Tente fazer sozinho! (Unifor-CE) Se a matriz b( ij ) de ordem 2, é a matriz inversa de , então: a) b 11 = - ½ b) b 12 = -1 c) b 21 = 1 d) b 22 = -1 e) b 22 = - ½

36. Solução Resposta: Letra B

37. Bibliografia Dante, Luiz Roberto – Matemática Contexto e Aplicações. 3ª edição – 2008. Editora Ática – SP. Páginas: 118 a 145. Iezzi, Gelson; Dolce, Osvaldo; Périgo, Roberto; Degenszajn, David – Matemática (volume único). 4ª edição – 2007. Editora Atual – SP. Páginas: 287 a 302. Bianchini, Edwaldo; Paccola, Herval – Curso de Matemática. 3ª edição – 2003. Editora Moderna – SP. Páginas: 283 a 308.