Matrizes
•Transferir como PPT, PDF•
3 gostaram•942 visualizações
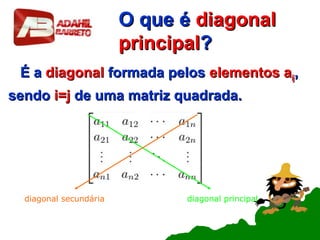
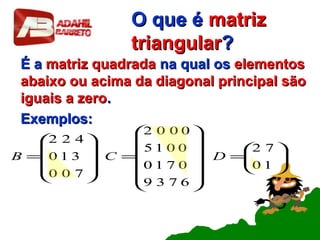
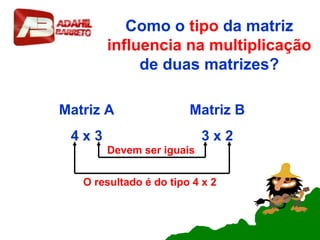
Este documento resume os principais conceitos sobre matrizes, incluindo: (1) definição de matriz e representação; (2) igualdade de matrizes; (3) tipos de matrizes como nula, linha, coluna, quadrada, diagonal, triangular, oposta e identidade; (4) operações como soma, subtração e multiplicação de matrizes.
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
Destaque
Destaque (20)
Semelhante a Matrizes
Semelhante a Matrizes (20)
Matrizes
- 1. Matrizes
- 2. Ao final dessa aula você saberá: O que é matriz e suas representações. Igualdade de matrizes. A definição de: matriz nula, matriz linha, matriz coluna, matriz quadrada, matriz diagonal, matriz triangular, matriz oposta, matriz identidade e matriz inversa. O que é diagonal principal e diagonal secundária. Soma, subtração e multiplicação de matrizes.
- 3. O que éO que é matrizmatriz?? É umaÉ uma tabelatabela de números que pode serde números que pode ser representadarepresentada entreentre chaveschaves ou entreou entre colchetescolchetes.. Exemplos:Exemplos: = = 104 321 104 321 AouA São matrizes com 2 linhas e 3 colunas. Então dizemos que é uma matriz 2 x 3.
- 4. Como é a representação genérica de uma matriz?
- 5. O que éO que é índiceíndice de umde um elemento?elemento? É a representação daÉ a representação da posiçãoposição que oque o elemento ocupa dentro da matriz.elemento ocupa dentro da matriz. Exemplo:Exemplo: O 3 é o elementoO 3 é o elemento aa1212, ou seja, está, ou seja, está nana 1ª linha1ª linha e nae na 2ª coluna2ª coluna.. = = 01 32 2221 1211 aa aa A
- 6. Quando duasQuando duas matrizesmatrizes AA e B sãoe B são iguaisiguais?? Quando os elementosQuando os elementos de mesmo índicede mesmo índice sãosão correspondentescorrespondentes.. Exemplo:Exemplo: 22222121 12121111 2221 1211 2221 1211 , ,,, baaa babaLogo ba bb B aa aa A == == == =
- 7. Tente fazer sozinho!Tente fazer sozinho! (PUC-MG)A matriz A = (a(PUC-MG)A matriz A = (aijij))2x32x3 é tal que:é tal que: É correto afirmar que:É correto afirmar que: =− ≠+ = jiseji jiseji aij ,32 ,3 − − − − − − −− = 927 651 ) 926 571 ) 96 25 71 ) 92 76 51 ) dc bAa
- 8. SoluçãoSolução aa1111 = 2.1 – 3.1 = 2 – 3 = -1= 2.1 – 3.1 = 2 – 3 = -1 aa1212 = 3.1 + 2 = 3+ 2 = 5= 3.1 + 2 = 3+ 2 = 5 aa1313 = 3.1 + 3 = 3 + 3 = 6= 3.1 + 3 = 3 + 3 = 6 aa2121 = 3.2 + 1 = 6 + 1 = 7= 3.2 + 1 = 6 + 1 = 7 aa2222 = 2.2 – 3.2 = 4 – 6 = -2= 2.2 – 3.2 = 4 – 6 = -2 aa2323 = 3.2 + 3 = 6 + 3 = 9= 3.2 + 3 = 6 + 3 = 9 Resposta: D 232221 131211 aaa aaa =− ≠+ = jiseji jiseji aij ,32 ,3
- 9. O que éO que é matriz linhamatriz linha?? É uma matriz formada porÉ uma matriz formada por apenas uma linhaapenas uma linha.. Exemplo:Exemplo: É uma matriz formada porÉ uma matriz formada por apenas uma colunaapenas uma coluna.. Exemplo:Exemplo: ( )70342=A O que éO que é matriz colunamatriz coluna?? = 9 0 2 B
- 10. O que éO que é matriz nulamatriz nula?? É uma matriz que apresentaÉ uma matriz que apresenta todostodos osos elementoselementos iguais aiguais a zerozero.. Exemplos:Exemplos: = = 000 000 0000 0000 0000 DC
- 11. O que éO que é matrizmatriz quadradaquadrada?? É a matriz que apresenta oÉ a matriz que apresenta o mesmo númeromesmo número dede linhas e colunaslinhas e colunas.. Exemplos:Exemplos: = 703 140 342 A Matriz 3 x 3 = 49 10 B Matriz 2 x 2 Dizemos que a matriz A é de ordem 3 e que a matriz B é de ordem 2.
- 12. O que éO que é diagonaldiagonal principalprincipal?? É aÉ a diagonaldiagonal formada pelosformada pelos elementos aelementos aijij,, sendosendo i=ji=j de uma matriz quadrada.de uma matriz quadrada. diagonal principaldiagonal secundária
- 13. Tente fazer sozinho! (Ufop-MG) Observe a matriz: Chama-se traço de uma matriz a soma dos elementos de sua diagonal principal. Determine x e y na matriz acima de tal forma que seu traço valha 9 e x seja o triplo de y. y x 00 40 321
- 14. Solução x = 3y 1 + 3y + y = 9 4y = 8 y = 2 x = 3.2 x = 6 y x 00 40 321
- 15. O que éO que é matrizmatriz diagonaldiagonal?? É aÉ a matriz quadradamatriz quadrada na qual todos osna qual todos os elementos que não pertencem a diagonalelementos que não pertencem a diagonal principal são iguais a zeroprincipal são iguais a zero. A. A diagonaldiagonal principalprincipal deve apresentardeve apresentar pelo menos umpelo menos um elemento diferente de zeroelemento diferente de zero.. Exemplos:Exemplos: = 700 010 002 A
- 16. O que éO que é matrizmatriz triangulartriangular?? É aÉ a matriz quadradamatriz quadrada na qual osna qual os elementoselementos abaixo ou acima da diagonal principal sãoabaixo ou acima da diagonal principal são iguais a zeroiguais a zero.. Exemplos:Exemplos: = = = 10 72 6739 0710 0015 0002 700 310 422 DCB
- 17. O que éO que é matrizmatriz opostaoposta?? É aÉ a matrizmatriz cujoscujos elementos são oselementos são os opostos de uma matriz dada.opostos de uma matriz dada. Exemplos:Exemplos: −− − =− − − = 732 410 732 410 AA − − =− − − = 52 81 52 81 BB
- 18. O que éO que é matrizmatriz transpostatransposta?? É aÉ a matrizmatriz cujascujas colunascolunas sãosão iguais àsiguais às linhas de uma matriz dada.linhas de uma matriz dada. Exemplo:Exemplo: − − = − − = 74 31 20 732 410 t AA Note que o número de linhas de A é o número de colunas de At . O mesmo acontece com o número de colunas A é 3x2 e At =2x3
- 19. Tente fazer sozinho! (UF-AM) Uma matriz quadrada é simétrica se, e somente se, At = A. Se a matriz É simétrica, então o valor de é: a) – 1 b) 3 c) 1 d) 4 e) 0 −− −= 131 501 2 2 y y xx A 3 yx +
- 20. Solução − − − = −− − 15 30 112 131 501 2 2 2 yx yx y y xx 112 ±=⇒= xx 1−=x 48235 =⇒−=−⇒−=− yyyy 1 3 3 3 41 3 == +− = + yx Resposta: letra c
- 21. O que éO que é matrizmatriz identidadeidentidade?? É aÉ a matriz quadradamatriz quadrada que apresentaque apresenta todos os elementos datodos os elementos da diagonal principaldiagonal principal iguais aiguais a 11 e ose os outrosoutros elementos iguais aelementos iguais a zerozero.. Exemplo:Exemplo: = = 10 01 100 010 001 23 II
- 22. Como somamos ou subtraímos matrizes? Basta somar ou subtrair os elementos correspondentes. As matrizes devem ser do mesmo tipo (m x n). Exemplos: = − − − − = − −− + − 4 3 10 3 5 1 7 8 9 ) 535 353 632 104 103 451 ) b a
- 23. Como multiplicamos uma matriz por um número real? Basta multiplicar todos os elementos da matriz por esse número real. Exemplo: − −− = − −− 06 33 156 02 11 52 3
- 24. Como o tipo da matriz influencia na multiplicação de duas matrizes? Matriz A 4 x 3 Matriz B 3 x 2 Devem ser iguais O resultado é do tipo 4 x 2
- 25. Como efetuamos o produto de duas matrizes? Dada uma matriz A = (aij)mxn e uma matriz B = (bij)nxp , o produto é uma matriz C = (cij)mxp, onde o elemento cij é calculado multiplicando ordenadamente os elementos da linha i, da matriz A, pelos elementos da coluna j, da matriz B, e somando os produtos obtidos.
- 28. Tente fazer sozinho! 1) (Mackenzie-SP) Se o produto de matrizes é a matriz nula, x + y é igual a: a) 0 b) 1 c) -1 d) 2 e) -2 − − 1 201 110 11 01 y x
- 29. Solução = − − 0 0 1 201 110 11 01 y x − − = − − 311 110 201 110 11 01
- 31. 2) (Fatec-SP) Seja a matriz , tal que . É verdade que a+b é igual a: a) 0 b) 1 c) 9 d) -1 e) -9 = 1 1 a b A − −− = 1910 8192 A
- 33. O que é matriz inversa? É matriz X de ordem n, cujo produto com a matriz A é igual a matriz identidade de ordem n. Ou seja, A.X = X.A = In, onde X = A-1 A matriz inversa de A É indicada por A-1 .
- 34. Exemplo: − − = = 25 13 35 12 BeA ( ) ( ) ( ) ( ) = +−−+ +−−+ = − − = 10 01 2.31.55.33.5 2.11.25.13.2 25 13 35 12 AB AB AB Logo, B = A-1
- 35. Tente fazer sozinho! (Unifor-CE) Se a matriz b(ij) de ordem 2, é a matriz inversa de , então: a) b11 = - ½ b) b12 = -1 c) b21 = 1 d) b22 = -1 e) b22 = - ½ − = 11 20 A
- 37. Bibliografia Dante, Luiz Roberto – Matemática Contexto e Aplicações. 5ª edição – 2013. Editora Ática – SP. Páginas: 96 a 119. Iezzi, Gelson; Dolce, Osvaldo; Périgo, Roberto; Degenszajn, David – Matemática (volume único). 4ª edição – 2007. Editora Atual – SP. Páginas: 287 a 302. Bianchini, Edwaldo; Paccola, Herval – Curso de Matemática. 3ª edição – 2003. Editora Moderna – SP. Páginas: 283 a 308.