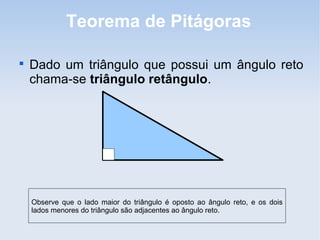
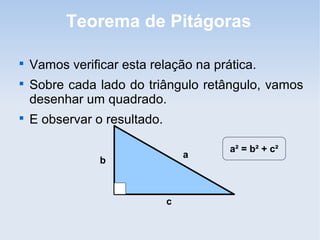
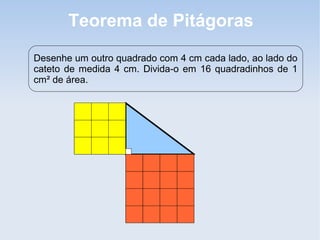
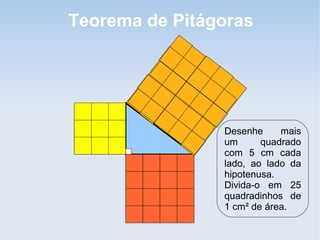
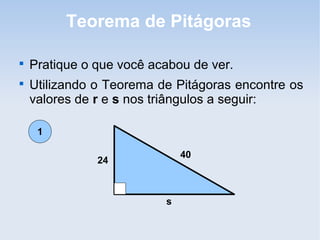
O documento explica o Teorema de Pitágoras, que estabelece que na qualquer triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Ele fornece exemplos para ilustrar a relação e instruções para que o leitor verifique a propriedade desenhando quadrados nos lados do triângulo.

1. Teorema de Pitágoras

Prof. Roberto
Informática Educativa II

2. Teorema de Pitágoras

Dado um triângulo que possui um ângulo reto
chama-se triângulo retângulo.
Observe que o lado maior do triângulo é oposto ao ângulo reto, e os dois
lados menores do triângulo são adjacentes ao ângulo reto.

3. Teorema de Pitágoras

Em todo triângulo retângulo, o lado maior, que
é o lado oposto ao ângulo reto, chama-se
hipotenusa; e os outros dois lados menores
chamam-se catetos.
hipotenusa
cateto
cateto

4. Teorema de Pitágoras

Os babilônios já sabiam que qualquer triângulo
cujos lados são proporcionais a 3, 4 e 5, é um
triângulo retângulo, como por exemplo.
3, 4, 5 6, 8, 10 9, 12, 15
12, 16, 20 15, 20, 25
Você mesmo, poderá comprovar, desenhando cuidadosamente um
triângulo, com lados de medidas 3 cm, 4 cm e 5 cm, verificando com
um transferidor que o ângulo oposto ao lado de 5cm mede 90°.
Observe que essa comprovação é apenas aproximada, pois ao medir
com o transferidor é muito provável que não meça exatamente 90°.

5. Teorema de Pitágoras

Os babilônicos descobriram, que em todo o
triângulo retângulo, a soma dos quadrados das
medidas dos catetos é igual ao quadrado da
medida da hipotenusa .
a
c
b
a² = b² + c²

6. Teorema de Pitágoras

Vamos verificar esta relação na prática.

Sobre cada lado do triângulo retângulo, vamos
desenhar um quadrado.

E observar o resultado.
a
c
b
a² = b² + c²

7. Teorema de Pitágoras
Desenhe um quadrado com 3 cm cada lado, ao lado do
cateto menor de medida 3 cm. Divida-o em 9 quadradinhos
de 1 cm² de área.

8. Teorema de Pitágoras
Desenhe um outro quadrado com 4 cm cada lado, ao lado do
cateto de medida 4 cm. Divida-o em 16 quadradinhos de 1
cm² de área.

9. Teorema de Pitágoras
Desenhe mais
um quadrado
com 5 cm cada
lado, ao lado da
hipotenusa.
Divida-o em 25
quadradinhos de
1 cm² de área.

10. Teorema de Pitágoras

Observe que a soma das áreas dos quadrados
menores é igual à área do quadrado maior.
9 16 25
Portanto, 3² + 4² = 5² → 9 + 16 = 25

11. Teorema de Pitágoras

Pratique o que você acabou de ver.

Utilizando o Teorema de Pitágoras encontre os
valores de r e s nos triângulos a seguir:
40
s
24
1

12. Teorema de Pitágoras
2
20
40
r
3
22
27,5
s
4
18
30
r

13. Teorema de Pitágoras

REFERÊNCIAS BIBLIOGRÁFICAS:

GUELLI, Oscar – Contando a História da Matemática - volume
1 – A Invenção dos números: Editora Ática.

RIBEIRO, Jackson e SOARES, Elizabeth – Construindo
Consciências Matemática – 8ª Série : Editora Scipione.

GUELLI, Oscar – EJA Educação de Jovens e Adultos – 7ª e 8ª
Séries : Editora Ática.