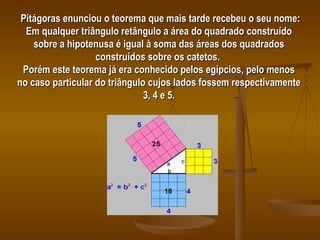
Pitágoras foi um matemático grego que descobriu o teorema que leva seu nome, o Teorema de Pitágoras. Este teorema estabelece que no triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. O documento apresenta a biografia de Pitágoras e exemplos de aplicações do teorema para calcular alturas de objetos geométricos como cones e pirâmides.

1. Teorema de Pitágoras

2. Bibliografia de Pitágoras Pitágoras foi um matemático, filósofo, astrônomo, músico e místico grego; nasceu na ilha de Samos, na Grécia. Na matemática, os estudos mais atribuídos a Pitágoras são: -o teorema do triângulo retângulo, a que chamamos Teorema de Pitágoras. -a descoberta dos irracionais ; Pitágoras foi o primeiro a enunciar e a demonstrar o teorema para todos os triângulos retângulos.

4. Pitágoras enunciou o teorema que mais tarde recebeu o seu nome: Em qualquer triângulo retângulo a área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os catetos. Porém este teorema já era conhecido pelos egípcios, pelo menos no caso particular do triângulo cujos lados fossem respectivamente 3, 4 e 5.

5. Aplicação do Teorema Pitágoras começou por estudar o teorema no plano, mas a aplicação do teorema em triângulos retângulos que se definem no espaço permite-nos resolver muitos outros problemas. Esta imagem que vêm ao lado é a região lagunar de Aveiro, é uma região belíssima, de horizontes amplos. Os habitantes desta região dedicaram-se durante largos séculos à extração do sal, por cristalização a partir da água salgada da ria. Em ambas as margens da ria erguiam-se os montes de sal . Suponha que um monte de sal é um modelo satisfatório de um cone de revolução.

6. Vamos desenhar um cone para exemplificar o monte de sal. Suponha que você tenha uma fita métrica. Como determinarias a altura do cone? Observe a figura acima e note que a altura o raio e a geratriz formam um triângulo retângulo. Sendo assim poderemos usar o teorema de Pitágoras para nos ajudar. Basta então obter a medida do raio e da geratriz para calcularmos.

7. Nos jardins do Museu do Louvre, em Paris, foi construída recentemente uma pirâmide quadrangular regular cujas faces laterais são em vidro. O lado da base tem 34 m e a altura da pirâmide é 22 m. Quantos metros de vidro foi necessária para a sua construção?

8. Resolução usando o teorema de Pitágoras

9. “ Todas as coisas são números. “ Pitágoras

10. Bibliografia Bibliografia de Pitágoras. Disponível em: http://www.suapesquisa.com/pesquisa/pitagoras.htm . Acessado em 20 de junho de 2009. Aplicações do Teorema de Pitágoras. Disponível em: www.prof2000.pt/ users / hjco / Pitagora /pg000010.htm . Acessado em 21 de junho de 2009.