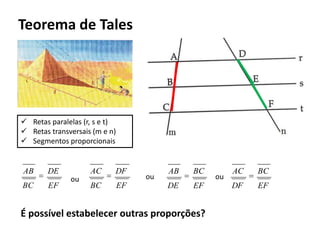
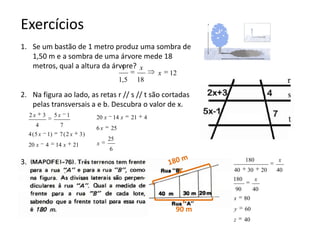
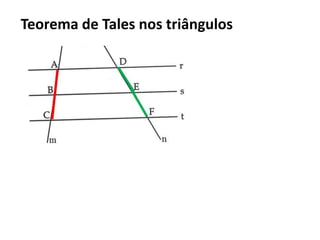
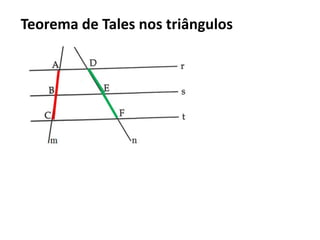
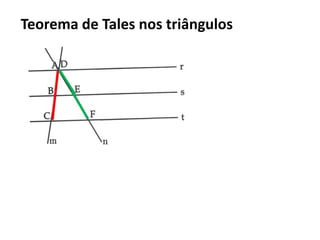
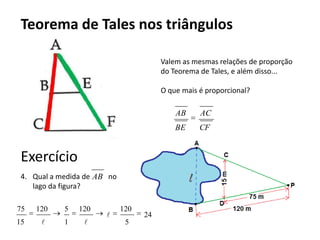
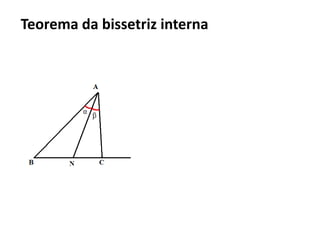
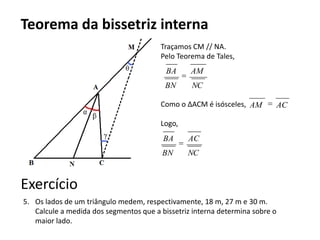
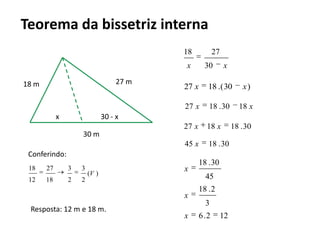
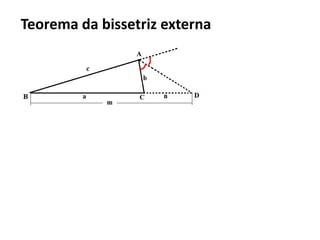
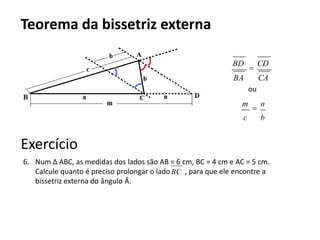
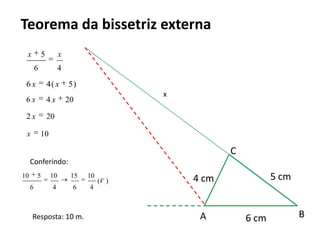
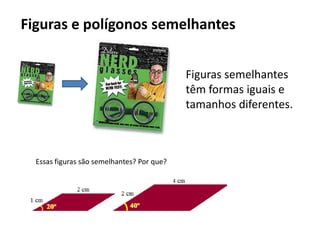
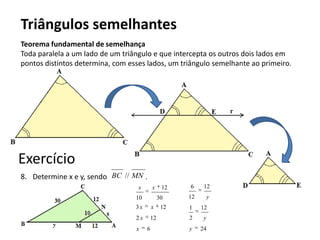
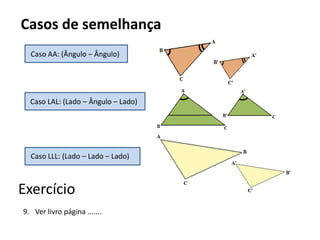
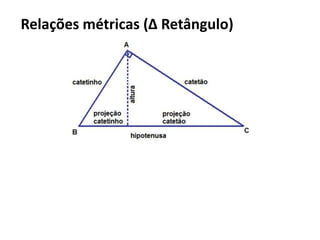
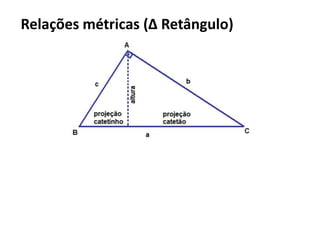
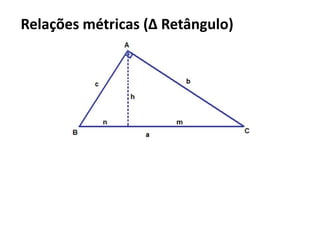
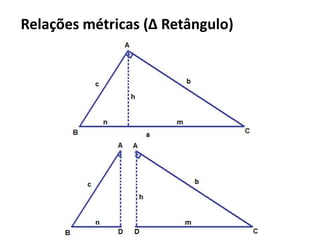
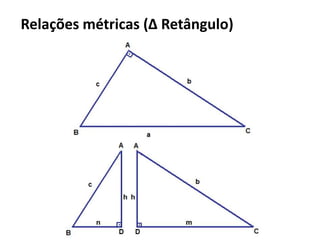
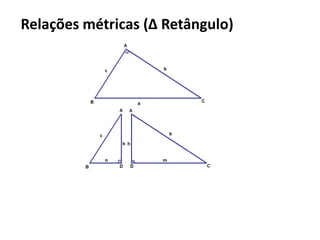
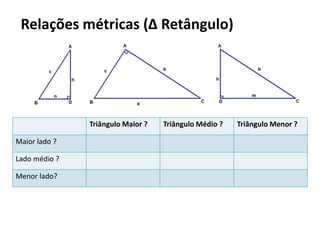
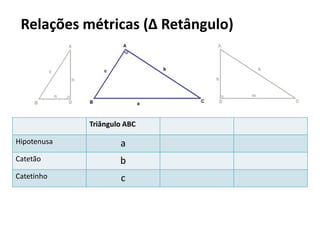
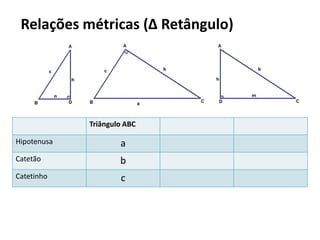
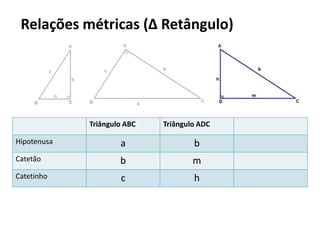
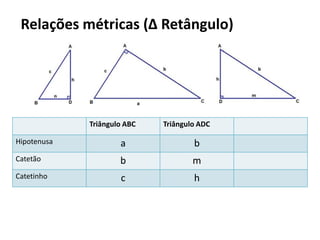
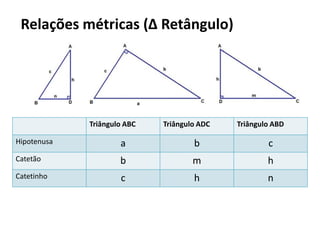
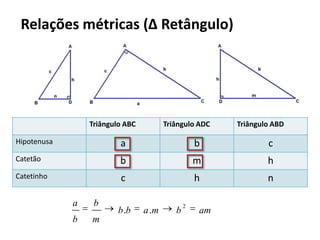
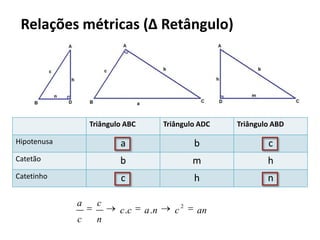
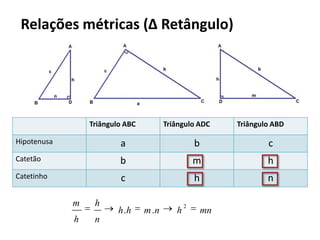
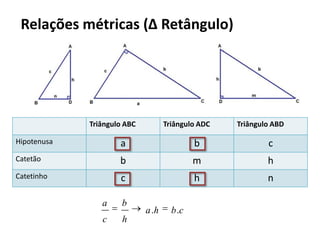
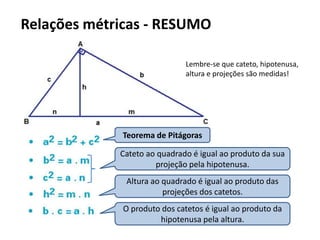
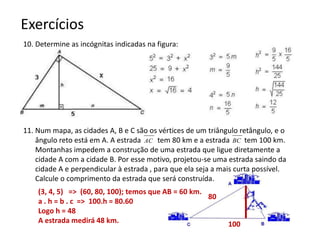
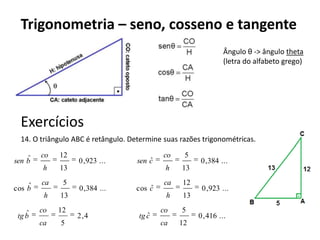
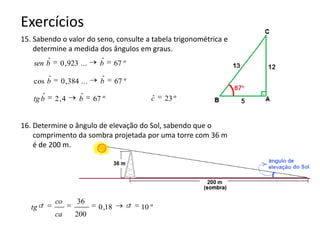
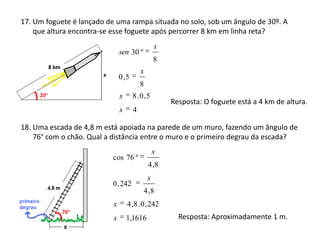
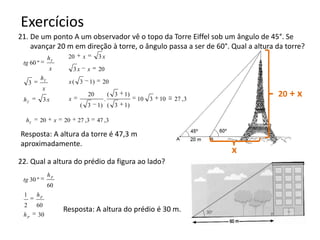
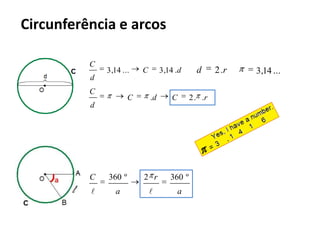
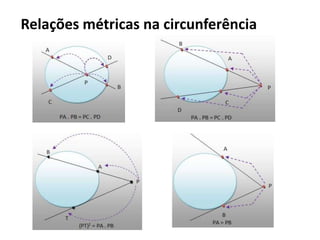
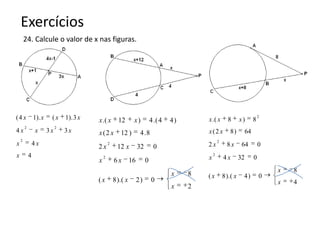
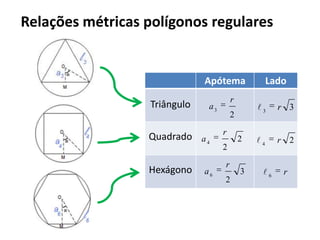
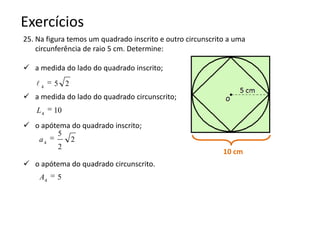
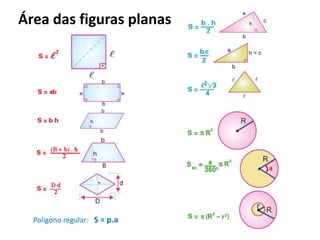
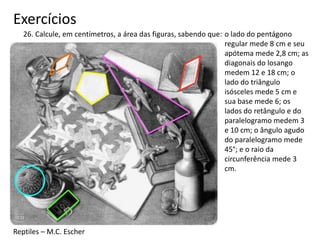
O documento resume os principais teoremas e conceitos de geometria analítica ensinados no 9o ano, incluindo Teorema de Tales, semelhança de figuras, trigonometria, áreas de polígonos e circunferências. Exercícios são fornecidos para aplicar esses conceitos.

1. Recuperaçãode Geometria9º ano - Escola NovaProf. Andréa Thees

2. Teorema de TalesRetas paralelas (r, s e t)

3. Retas transversais (m e n)

4. Segmentos proporcionaisouououÉ possível estabelecer outras proporções?

5. ExercíciosSe um bastão de 1 metro produz uma sombra de 1,50 m e a sombra de uma árvore mede 18 metros, qual a altura da árvore?Na figura ao lado, as retas r // s // t são cortadas pelas transversais a e b. Descubra o valor de x.180 m90 m

6. Teorema de Tales nos triângulos

7. Teorema de Tales nos triângulos

8. Teorema de Tales nos triângulos

9. Teorema de Tales nos triângulosValem as mesmas relações de proporção do Teorema de Tales, e além disso...O que mais é proporcional?ExercícioQual a medida de no lago da figura?

10. Teorema da bissetriz interna

11. Teorema da bissetriz internaTraçamos CM // NA.Pelo Teorema de Tales,Como o ΔACM é isósceles, Logo,ExercícioOs lados de um triângulo medem, respectivamente, 18 m, 27 m e 30 m. Calcule a medida dos segmentos que a bissetriz interna determina sobre o maior lado.

12. Teorema da bissetriz interna27 m18 mx30 - x30 mConferindo:Resposta: 12 m e 18 m.

13. Teorema da bissetriz externa

14. Teorema da bissetriz externaouExercícioNum Δ ABC, as medidas dos lados são AB = 6 cm, BC = 4 cm e AC = 5 cm. Calcule quanto é preciso prolongar o lado , para que ele encontre a bissetriz externa do ângulo Â.

15. Teorema da bissetriz externaC5 cm4 cmx6 cmBAConferindo:Resposta: 10 m.

16. Figuras e polígonos semelhantesFiguras semelhantes têm formas iguais e tamanhos diferentes.Essas figuras são semelhantes? Por que?

17. Figuras e polígonos semelhantesDois polígonos são semelhantes quando os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais. E a razão entre seus perímetros é igual à razão entre dois lados correspondentes (ou homólogos).

18. Figuras e polígonos semelhantesDois polígonos são semelhantes quando os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais. E a razão entre seus perímetros é igual à razão entre dois lados correspondentes (ou homólogos).ExercícioAs pétalas da flor pentágono são congruentes e medem 3 cm aproximadamente. Ao ampliar a foto, as pétalas passaram a medir 5 cm. Calcule a razão de semelhança. O que você pode concluir em relação aos perímetros das duas flores?

19. Triângulos semelhantesTeorema fundamental de semelhançaToda paralela a um lado de um triângulo e que intercepta os outros dois lados em pontos distintos determina, com esses lados, um triângulo semelhante ao primeiro.ExercícioDetermine x e y, sendo .

20. Casos de semelhançaCaso AA: (Ângulo – Ângulo)Caso LAL: (Lado – Ângulo – Lado)Caso LLL: (Lado – Lado – Lado)ExercícioVer livro página .......

21. Relações métricas (Δ Retângulo)

22. Relações métricas (Δ Retângulo)

23. Relações métricas (Δ Retângulo)

24. Relações métricas (Δ Retângulo)

25. Relações métricas (Δ Retângulo)

26. Relações métricas (Δ Retângulo)

27. Relações métricas (Δ Retângulo)

28. Relações métricas (Δ Retângulo)

29. Relações métricas (Δ Retângulo)

30. Relações métricas (Δ Retângulo)

31. Relações métricas (Δ Retângulo)

32. Relações métricas (Δ Retângulo)

33. Relações métricas (Δ Retângulo)

34. Relações métricas (Δ Retângulo)

35. Relações métricas (Δ Retângulo)

36. Relações métricas (Δ Retângulo)

37. Relações métricas (Δ Retângulo)

38. Relações métricas - RESUMOLembre-se que cateto, hipotenusa, altura e projeções são medidas!Teorema de PitágorasCateto ao quadrado é igual ao produto da sua projeção pela hipotenusa.Altura ao quadrado é igual ao produto das projeções dos catetos.O produto dos catetos é igual ao produto da hipotenusa pela altura.

39. ExercíciosDetermine as incógnitas indicadas na figura:Num mapa, as cidades A, B e C são os vértices de um triângulo retângulo, e o ângulo reto está em A. A estrada tem 80 km e a estrada tem 100 km. Montanhas impedem a construção de uma estrada que ligue diretamente a cidade A com a cidade B. Por esse motivo, projetou-se uma estrada saindo da cidade A e perpendicular à estrada , para que ela seja a mais curta possível. Calcule o comprimento da estrada que será construída.(3, 4, 5) => (60, 80, 100); temos que AB = 60 km.a . h = b . c => 100.h = 80.60Logo h = 48A estrada medirá 48 km.80100

40. TrigonometriaEla está em todo lugar!

41. Trigonometria – seno, cosseno e tangenteÂngulo θ -> ângulo theta (letra do alfabeto grego)ExercíciosO triângulo ABC é retângulo. Determine suas razões trigonométricas.

42. ExercíciosSabendo o valor do seno, consulte a tabela trigonométrica e determine a medida dos ângulos em graus. Determine o ângulo de elevação do Sol, sabendo que o comprimento da sombra projetada por uma torre com 36 m é de 200 m.

43. Um foguete é lançado de uma rampa situada no solo, sob um ângulo de 30º. A que altura encontra-se esse foguete após percorrer 8 km em linha reta?Uma escada de 4,8 m está apoiada na parede de um muro, fazendo um ângulo de 76° com o chão. Qual a distância entre o muro e o primeiro degrau da escada?Resposta: O foguete está a 4 km de altura.Resposta: Aproximadamente 1 m.

44. Resposta: A altura das nuvens é de 5,6 km.xResposta: O ponta A está a 52,2 m do solo.

45. Razões trigonométricas de 30°, 45° e 60°

46. ExercíciosDe um ponto A um observador vê o topo da Torre Eiffel sob um ângulo de 45°. Se avançar 20 m em direção à torre, o ângulo passa a ser de 60°. Qual a altura da torre?Qual a altura do prédio da figura ao lado?20 + xResposta: A altura da torre é 47,3 maproximadamente.xResposta: A altura do prédio é 30 m.

47. Circunferência e arcos

48. Relações métricas na circunferência

49. ExercíciosO sino do relógio mais preciso do mundo, o Big Ben, fica na Torre de Santo Estéfano, em Londres, na Inglaterra. Os ponteiros desse relógio são enormes e medem dois metros e setenta centímetros, o das horas, e quatro metros e trinta centímetros, o dos minutos. Qual é a distância que a ponta de cada ponteiro percorre num intervalo de tempo de 6 horas?Resposta: Aproximadamente 8,5 m o ponteiro das horas e 162m o ponteiro dos minutos.

50. ExercíciosCalcule o valor de x nas figuras.

51. Relações métricas polígonos regulares

52. ExercíciosNa figura temos um quadrado inscrito e outro circunscrito a uma circunferência de raio 5 cm. Determine:a medida do lado do quadrado inscrito;

53. a medida do lado do quadrado circunscrito;

54. o apótema do quadrado inscrito;

55. o apótema do quadrado circunscrito.10 cm