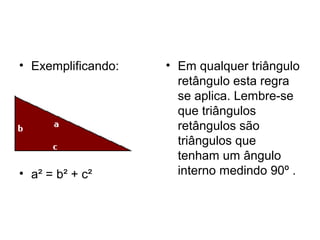
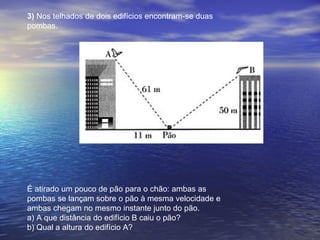
O documento descreve o Teorema de Pitágoras, que relaciona os lados de um triângulo retângulo. A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Exemplos e exercícios são fornecidos para ilustrar a aplicação deste teorema fundamental da matemática.

1. RELAÇÃO MÉTRICA NO
TRIÂNGULO RETÂNGULO
TEOREMA DE PITÁGORAS

2. O Teorema de PitágorasO Teorema de Pitágoras
talvez seja o mais importantetalvez seja o mais importante
teorema de toda ateorema de toda a
matemática. Com ele pode-sematemática. Com ele pode-se
descobrir a medida de umdescobrir a medida de um
lado de um triângulolado de um triângulo
retângulo, a partir daretângulo, a partir da
medida de seus outros doismedida de seus outros dois
lados.lados.

3. A soma dos
quadrados dos
catetos é igual ao
quadrado da
hipotenusa.

4. • Exemplificando:
• a² = b² + c²
• Em qualquer triângulo
retângulo esta regra
se aplica. Lembre-se
que triângulos
retângulos são
triângulos que
tenham um ângulo
interno medindo 90º .

5. • É possível utilizar a regra
de Pitágoras em
praticamente todas as
figuras geométricas
planas, pois, de alguma
forma elas podem ser
divididos em triângulos.
Por exemplo um
quadrado. Podemos
determinar a medida da
bissetriz de um ângulo
interno usando a mesma
fórmula, basta perceber
que a bissetriz seria a
hipotenusa de um
triângulo inscrito no
quadrado:
• Assim, h² mediria:
• a²+b²

6. ExercíciosExercícios
1 - A figura representa um barco à vela.
Determine, de acordo com os dados da figura,
os valores de

7. 2) Qual a altura do poste?

8. 3) Nos telhados de dois edifícios encontram-se duas
pombas.
É atirado um pouco de pão para o chão: ambas as
pombas se lançam sobre o pão à mesma velocidade e
ambas chegam no mesmo instante junto do pão.
a) A que distância do edifício B caiu o pão?
b) Qual a altura do edifício A?