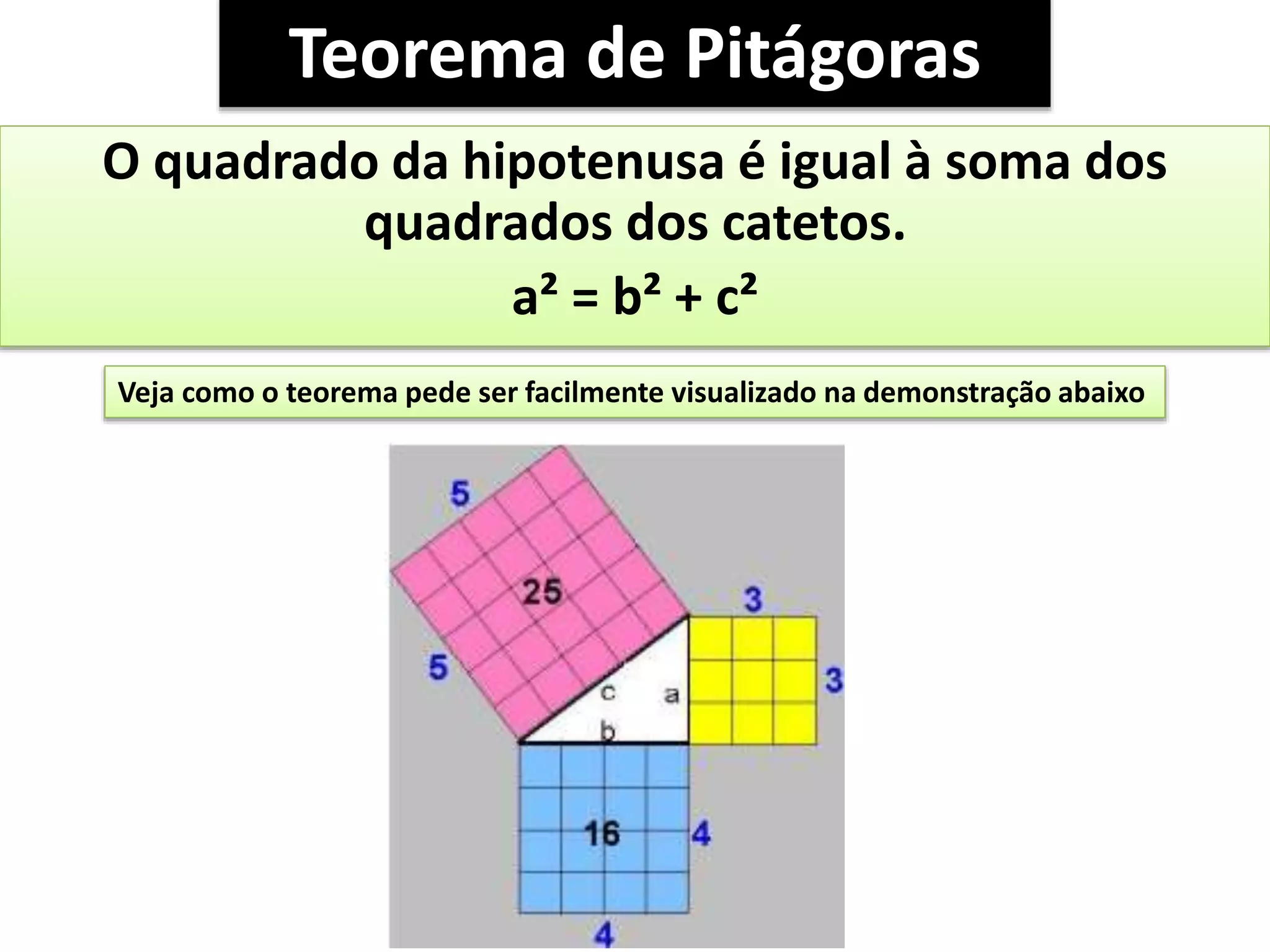
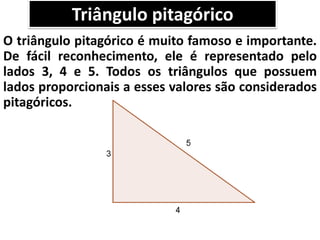
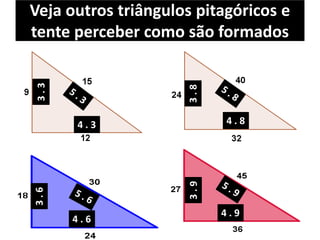
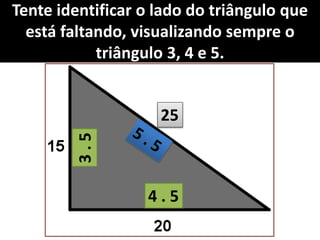
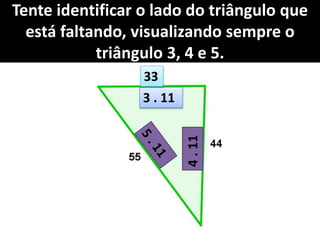
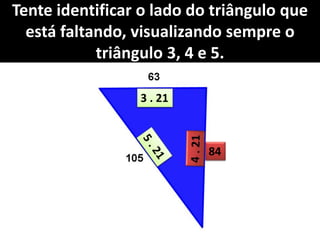
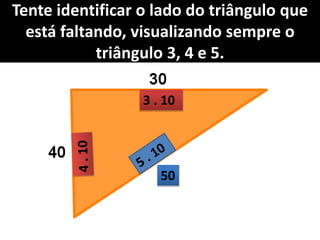
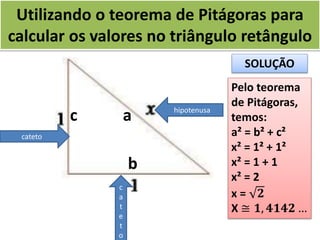
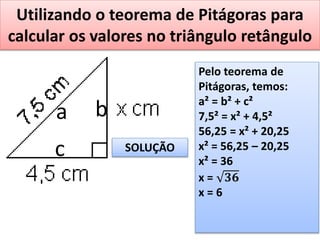
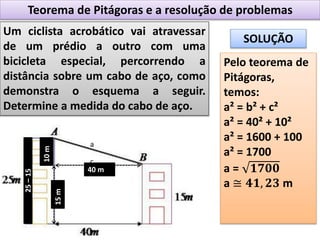
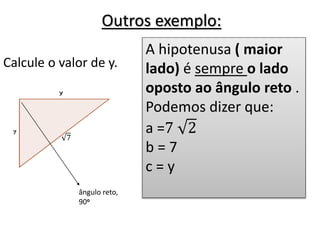
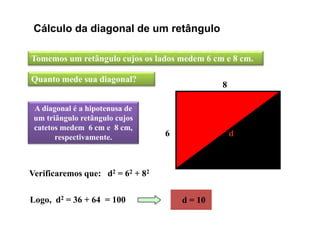
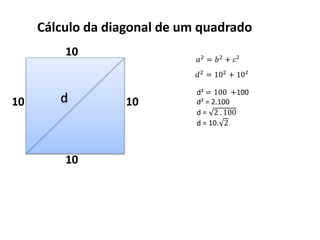
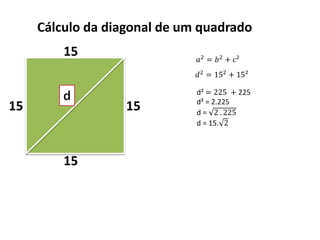
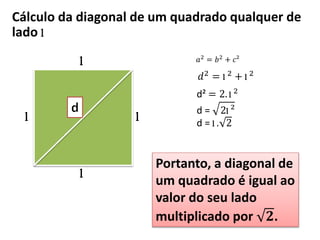
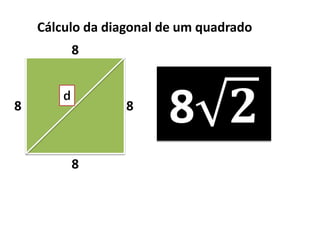
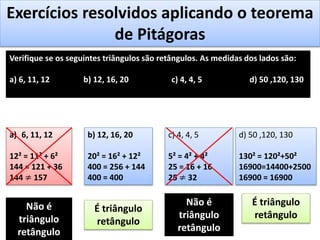
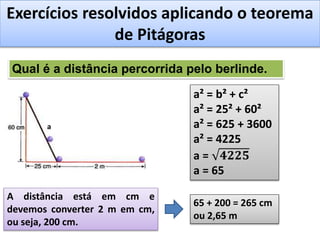
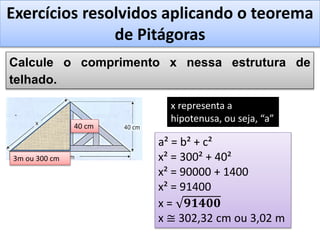
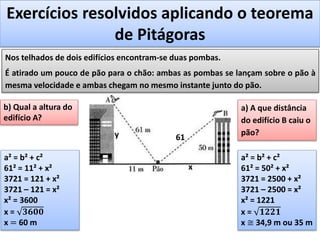
O documento aborda o teorema de Pitágoras, que afirma que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos em um triângulo retângulo. Diversos exemplos e exercícios são apresentados para ilustrar a aplicação do teorema na determinação de lados e diagonais de várias figuras geométricas. Além disso, são discutidos problemas práticos que utilizam o teorema para resolver situações cotidianas.

1. Teorema de Pitágoras
O quadrado da hipotenusa é igual à soma dos
quadrados dos catetos.
a² = b² + c²
Veja como o teorema pede ser facilmente visualizado na demonstração abaixo

2. Triângulo pitagórico
O triângulo pitagórico é muito famoso e importante.
De fácil reconhecimento, ele é representado pelo
lados 3, 4 e 5. Todos os triângulos que possuem
lados proporcionais a esses valores são considerados
pitagóricos.

3. Veja outros triângulos pitagóricos e
tente perceber como são formados3.3
4 . 3
3.8
4 . 8
3.6
4 . 6
3.9
4 . 9

4. Tente identificar o lado do triângulo que
está faltando, visualizando sempre o
triângulo 3, 4 e 5.
3.5
4 . 5
25

5. Tente identificar o lado do triângulo que
está faltando, visualizando sempre o
triângulo 3, 4 e 5.
4.11
3 . 11
33

6. Tente identificar o lado do triângulo que
está faltando, visualizando sempre o
triângulo 3, 4 e 5.
3 . 21
84

7. Tente identificar o lado do triângulo que
está faltando, visualizando sempre o
triângulo 3, 4 e 5.
3 . 10
50

8. Utilizando o teorema de Pitágoras para
calcular os valores no triângulo retângulo
hipotenusa
c
a
t
e
t
o
cateto
ac
b
SOLUÇÃO
Pelo teorema
de Pitágoras,
temos:
a² = b² + c²
x² = 1² + 1²
x² = 1 + 1
x² = 2
x = 𝟐
X ≅ 𝟏, 𝟒𝟏𝟒𝟐 …

9. Utilizando o teorema de Pitágoras para
calcular os valores no triângulo retângulo
a b
c
Pelo teorema de
Pitágoras, temos:
a² = b² + c²
7,5² = x² + 4,5²
56,25 = x² + 20,25
x² = 56,25 – 20,25
x² = 36
x = 𝟑𝟔
x = 6
SOLUÇÃO

10. Teorema de Pitágoras e a resolução de problemas
Um ciclista acrobático vai atravessar
de um prédio a outro com uma
bicicleta especial, percorrendo a
distância sobre um cabo de aço, como
demonstra o esquema a seguir.
Determine a medida do cabo de aço.
SOLUÇÃO
Pelo teorema de
Pitágoras,
temos:
a² = b² + c²
a² = 40² + 10²
a² = 1600 + 100
a² = 1700
a = 𝟏𝟕𝟎𝟎
a ≅ 𝟒𝟏, 𝟐𝟑 m
a
c
b
40 m
15m
25–15
10m

11. Teorema de Pitágoras e a resolução de problemas
Analisando o trapézio
isósceles, determine a
medida “x” , o perímetro
e sua área.
Obs.: Trapézio isósceles é o quadrilátero
que possui os dois lados não paralelos
iguais
20 – 14
33 14
33 14
Como já vimos anteriormente, temos o
triângulo pitagórico 3, 4 e x = 5.
55
Perímetro  é a soma de
todos os lados de uma figura
O perímetro do trapézio
isósceles é:
P = 14 + 5 + 20 + 5
P = 44
A área é calculada pela
fórmula: 𝑨 =
𝑩+𝒃 .𝒉
𝟐
𝑨 =
𝟐𝟎 + 𝟏𝟒 . 𝟒
𝟐
𝑨 =
𝟑𝟒 . 𝟒
𝟐
𝑨 =
𝟏𝟑𝟔
𝟐
= 𝟔8

12. Calcule o valor de y.
Outros exemplo:
A hipotenusa ( maior
lado) é sempre o lado
oposto ao ângulo reto .
Podemos dizer que:
a =7 2
b = 7
c = y
7
ângulo reto,
90o

13. → y = +7 ou – 7 ------ como não tem como uma distância ser negativa o valor de y será:
y = 7.
Aplicando o teorema de Pitágoras, temos: 𝒂 𝟐
= 𝒃 𝟐
+ 𝒄 𝟐
→ 𝟕 𝟐
𝟐
= 𝟕 𝟐 + 𝒚 𝟐
→ 49. 2 = 49 + y2
→ 98 = 49 + y2 --------- como queremos achar o valor de y devemos isolá-lo
em um lado da igualdade. Para isso o 49 passará para o outro membro da
igualdade com a operação inversa.
→ 98 – 49 = y2
→ y² = 49 ------- agora a potência do y passará para o outro membro da
igualdade com a operação inversa (radiciação).
→ 𝐲 = ± 𝟒𝟗

14. Cálculo da diagonal de um retângulo
Tomemos um retângulo cujos os lados medem 6 cm e 8 cm.
A diagonal é a hipotenusa de
um triângulo retângulo cujos
catetos medem 6 cm e 8 cm,
respectivamente.
Logo, d2 = 36 + 64 = 100
Quanto mede sua diagonal?
6
8
d
Verificaremos que: d2 = 62 + 82
d = 10

15. Cálculo da diagonal de um quadrado
6
6
6
6
𝑎2 = 𝑏2 + 𝑐²
𝑑2
= 62
+ 6²
d
d² = 36 + 36
d² = 2.36
d = 2 . 36
d = 6. 2
𝒏
𝒂
𝒏
= 𝒂

16. Cálculo da diagonal de um quadrado
d10 10
10
10
𝑎2 = 𝑏2 + 𝑐²
𝑑2
= 102
+ 10²
d² = 100 +100
d² = 2.100
d = 2 . 100
d = 10. 2

17. Cálculo da diagonal de um quadrado
15
1515
15
𝑎2 = 𝑏2 + 𝑐²
𝑑2
= 152
+ 15²
d² = 225 + 225
d² = 2.225
d = 2 . 225
d = 15. 2

18. Cálculo da diagonal de um quadrado qualquer de
lado l
l
l
l
l
𝑎2 = 𝑏2 + 𝑐²
𝑑2
= l 2
+ l 2
d² = 2. l 2
d = 2l ²
d = l . 2
Portanto, a diagonal de
um quadrado é igual ao
valor do seu lado
multiplicado por 𝟐.

19. Cálculo da diagonal de um quadrado
8
8
8 𝟐88

20. Exercícios resolvidos aplicando o teorema
de Pitágoras
Verifique se os seguintes triângulos são retângulos. As medidas dos lados são:
a) 6, 11, 12 b) 12, 16, 20 c) 4, 4, 5 d) 50 ,120, 130
a) 6, 11, 12
12² = 11² + 6²
144 = 121 + 36
144 ≠ 157
Não é
triângulo
retângulo
b) 12, 16, 20
20² = 16² + 12²
400 = 256 + 144
400 = 400
É triângulo
retângulo
c) 4, 4, 5
5² = 4² + 4²
25 = 16 + 16
25 ≠ 32
Não é
triângulo
retângulo
d) 50 ,120, 130
130² = 120²+50²
16900=14400+2500
16900 = 16900
É triângulo
retângulo

21. Exercícios resolvidos aplicando o teorema
de Pitágoras
Qual é a distância percorrida pelo berlinde.
a
a² = b² + c²
a² = 25² + 60²
a² = 625 + 3600
a² = 4225
a = 𝟒𝟐𝟐𝟓
a = 65
A distância está em cm e
devemos converter 2 m em cm,
ou seja, 200 cm.
65 + 200 = 265 cm
ou 2,65 m

22. Exercícios resolvidos aplicando o teorema
de Pitágoras
O Pedro e o João brincam de gangorra, como indica
a figura:
A altura máxima que
pode subir cada um
dos amigos é de 60
cm. Qual o
comprimento da
gangorra?
60cm
180cm
a² = b² + c²
a² = 180² + 60²
a² = 32400 + 3600
a² = 36000
a = 𝟑𝟔𝟎𝟎𝟎
a ≅ 189,7 cm ou 1,89m
a

23. Exercícios resolvidos aplicando o teorema
de Pitágoras
Calcule o comprimento x nessa estrutura de
telhado.
40 cm
3m ou 300 cm
x representa a
hipotenusa, ou seja, “a”
a² = b² + c²
x² = 300² + 40²
x² = 90000 + 1400
x² = 91400
x = 𝟗𝟏𝟒𝟎𝟎
x ≅ 302,32 cm ou 3,02 m

24. (Uflavras 2000) Qual deve ser a altitude do
balão para que sua distância ao topo do
prédio seja de 10 km?
Exercícios resolvidos aplicando o teorema
de Pitágoras
8 km
h
a² = b² + c²
10² = h² + 8²
100 = h² + 64
100 – 64 = h²
h² = 36
h = 𝟑𝟔
h = 6 km ou 6000 m
Somando a altura do
prédio, temos:
6000 + 200 = 6200 m
Pelo
triângulo
pitagórico,
temos:
5 . 2
3 . 2
4 . 2
Ou calculando
pelo teorema de
Pitágoras, temos:

25. Exercícios resolvidos aplicando o teorema
de Pitágoras
Nos telhados de dois edifícios encontram-se duas pombas.
É atirado um pouco de pão para o chão: ambas as pombas se lançam sobre o pão à
mesma velocidade e ambas chegam no mesmo instante junto do pão.
a) A que distância
do edifício B caiu o
pão?
61
a² = b² + c²
61² = 50² + x²
3721 = 2500 + x²
3721 – 2500 = x²
x² = 1221
x = 𝟏𝟐𝟐𝟏
x ≅ 34,9 m ou 35 m
x
b) Qual a altura do
edifício A?
y
a² = b² + c²
61² = 11² + x²
3721 = 121 + x²
3721 – 121 = x²
x² = 3600
x = 𝟑𝟔𝟎𝟎
x = 60 m