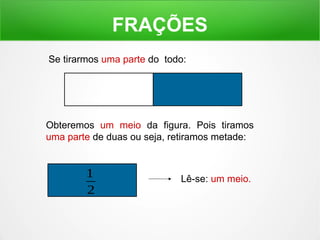
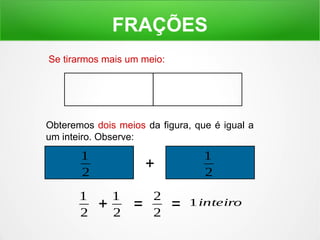
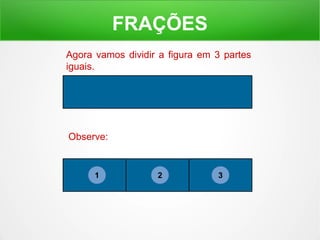
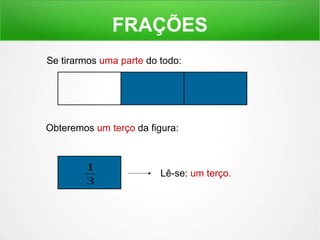
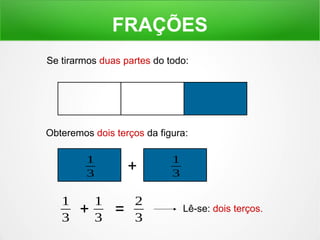
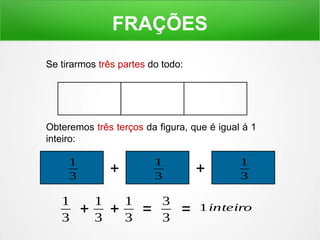
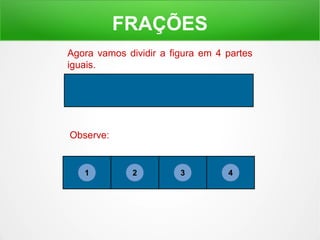
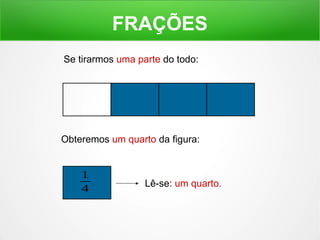
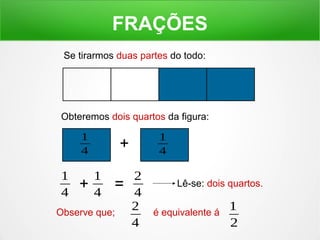
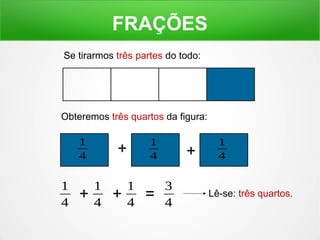
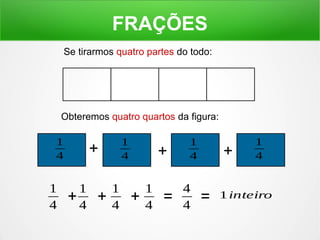
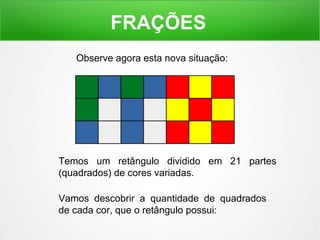
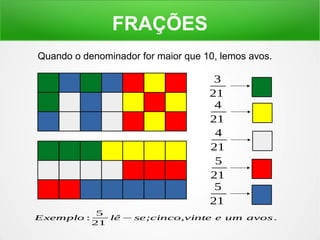
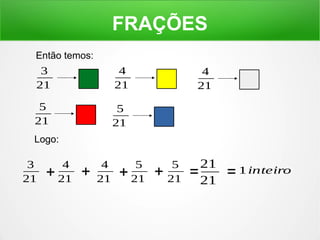
O documento explica o conceito de frações, dividindo figuras geométricas em partes iguais e identificando quantas partes são retiradas do todo. É mostrado como ler frações como "um meio", "dois terços" e como a soma de frações pode resultar em um inteiro.

1. •Matemática
•Frações
•Prof. Roberto
• Visite meu blog:
• www.betontem.blogspot.com.br

2. FRAÇÕES
A fração envolve a ideia de alguma coisa que foi
dividida em partes iguais. Dentre essas partes,
consideramos uma ou algumas, de acordo com o
nosso interesse.
Observe a figura:
Vamos dividi-la em 2 partes iguais:
1 2

3. FRAÇÕES
Se tirarmos uma parte do todo:
Obteremos um meio da figura. Pois tiramos
uma parte de duas ou seja, retiramos metade:
1 Lê-se: um meio.
2

4. FRAÇÕES
Se tirarmos mais um meio:
Obteremos dois meios da figura, que é igual a
um inteiro. Observe:
1 +
2
1
2
1
2 + 1
2 = 2
2 = 1inteiro

5. FRAÇÕES
Agora vamos dividir a figura em 3 partes
iguais.
Observe:
1 2 3

6. FRAÇÕES
Se tirarmos uma parte do todo:
Obteremos um terço da figura:
1 Lê-se: um terço.
3

7. FRAÇÕES
Se tirarmos duas partes do todo:
Obteremos dois terços da figura:
Lê-se: dois terços.
1
3
1
3 +
1
3 + 1
3 = 2
3

8. FRAÇÕES
Se tirarmos três partes do todo:
Obteremos três terços da figura, que é igual á 1
inteiro:
1
3
1
3 +
1
3 + 1
3 = 3
3
1
3 +
+ 1
3 = 1inteiro

9. FRAÇÕES
Agora vamos dividir a figura em 4 partes
iguais.
Observe:
1 2 3 4

10. FRAÇÕES
Se tirarmos uma parte do todo:
Obteremos um quarto da figura:
Lê-se: um quarto.
1
4

11. FRAÇÕES
Se tirarmos duas partes do todo:
Obteremos dois quartos da figura:
Lê-se: dois quartos.
1
4 + 1
4
1
4 + 1
4 = 2
4
Observe que; 2
4
1
2
é equivalente á

12. FRAÇÕES
Se tirarmos três partes do todo:
Obteremos três quartos da figura:
Lê-se: três quartos.
1
4 + 1
4
1
4 + 1
4 = 3
4
+ 1
4
+ 1
4

13. FRAÇÕES
Se tirarmos quatro partes do todo:
Obteremos quatro quartos da figura:
1
4 + 1
4
+ 1
4
1
+ 1
+ 1
= 4
4 4 4
4
+ 1
4
1
4 + = 1inteiro

14. FRAÇÕES
Observe agora esta nova situação:
Temos um retângulo dividido em 21 partes
(quadrados) de cores variadas.
Vamos descobrir a quantidade de quadrados
de cada cor, que o retângulo possui:

15. FRAÇÕES
Quando o denominador for maior que 10, lemos avos.
3
21
4
21
4
21
5
21
5
21
Exemplo : 5
21
lê−se;cinco,vinte e um avos.

16. FRAÇÕES
3
21
4
21
4
21
5
21
5
21
Então temos:
Logo:
3
21
+ 4
+ 4
21
21
+ 5
+ 5
=21
21
21 21 =1inteiro

17. Conclusão:
Observamos, que trabalhar com fração,
é dividir algo ou alguma coisa em partes
iguais. O que não é difícil de entender,
basta termos atenção ao lidarmos com
estas partes de forma correta, quando
fizermos algum cálculo que envolva as
mesmas.

18. Atividade elaborada pelo:
Prof. Roberto
Disciplina Matemática.
Visite meu blog:
www.betontem.blogspot.com.br