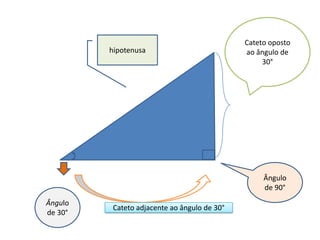
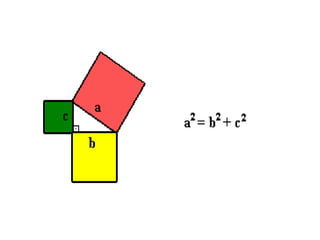
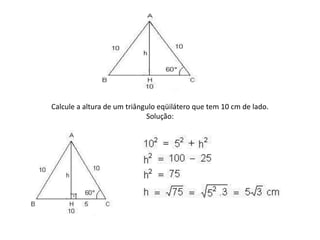
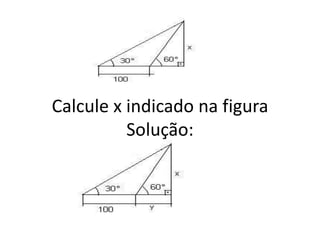
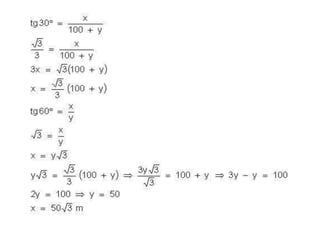O documento discute trigonometria em triângulos retângulos, definindo seus lados como hipotenusa e catetos, e apresenta as funções trigonométricas básicas de seno, cosseno e tangente. Também apresenta o Teorema de Pitágoras e exemplos de exercícios resolvidos usando conceitos de trigonometria.

1. PorKeilaRodrigues CarvalhoRio Bonito

2. Trigonometria no Triângulo Retângulo

3. Lados do Triângulo RetânguloOs lados de um triângulo retângulo recebem nomes especiais. Estes nomes são dados de acordo com a posição em relação ao ângulo reto. O lado oposto ao ângulo reto é a hipotenusa. Os lados que formam o ângulo reto (adjacentes a ele) são os catetos.

4. A trigonometria possui uma infinidade de aplicações práticas. Desde a antiguidade já se usava da trigonometria para obter distâncias impossíveis de serem calculadas por métodos comuns.

5. Triângulo Retângulo

6. É um triângulo que possui um ângulo reto, isto é, um dos seus ângulos mede noventa graus, daí o nome triângulo retângulo. Como a soma das medidas dos ângulos internos de um triângulo é igual a 180°, então a soma dos outros dois ângulos medirão 90°.

7. Cateto oposto ao ângulo de 30°hipotenusaÂngulo de 90°Ângulo de 30°Cateto adjacente ao ângulo de 30°

8. Os catetos recebem nomes especiais de acordo com a sua posição em relação ao ângulo sob análise. Se estivermos operando com o ângulo 30°, então o lado oposto a esse ângulo é o cateto oposto ao ângulo de 30° e o lado adjacente ao ângulo 30°, que fica ao lado, é o cateto adjacente ao ângulo de 30°.

9. Funções trigonométricas básicas

10. Seno = medida do cateto oposto medida da hipotenusa cos = medida do cateto adjacente medida da hipotenusatang = medida do cateto oposto medida do cateto adjacente

11. O Teorema de Pitágoras diz que, em um triângulo retângulo, o quadrado da hipotenusa é igualà soma dos quadrados dos catetos. Se construírmos quadrados sobre os lados a, b e c do triângulo retângulo, esses quadrados terão área a2, b2 e c2.Assim podemos enunciar o Teorema de Pitágoras da seguinte forma:

13. Desafios

14. Calcule a altura de um triângulo eqüilátero que tem 10 cm de lado.Solução:

15. 1) Calcule o perímetro do triângulo retângulo ABC da figura, sabendo que o segmento BC é igual a 10 m e cos α = 3/5 Exercícios resolvidos:1) Calcule o perímetro do triângulo retângulo ABC da figura, sabendo que o segmento BC é igual a 10 m e cos α = 3/5 Solução:

16. Calcule x indicado na figuraSolução:

18. Uma escada apoiada em uma parede, num ponto distante 4 m dos solo, forma com essa parede um ângulo de 60°. Qual é o comprimento da escada em metros? Solução:

19. Referênciashttp://quimsigaud.tripod.com/trianguloretangulo/http://www.colegiocatanduvas.com.br/desgeo/teopitago/index.htmhttp://pessoal.sercomtel.com.br/matematica/trigonom/trigon1/mod114.htm