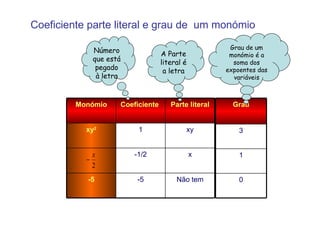
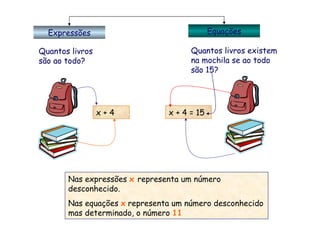
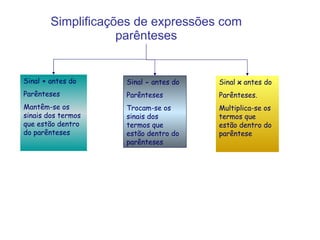
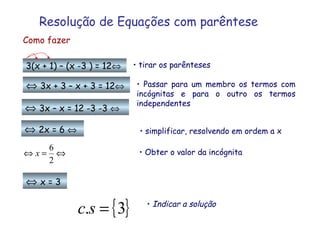
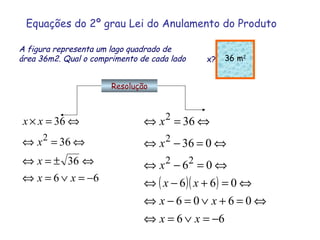
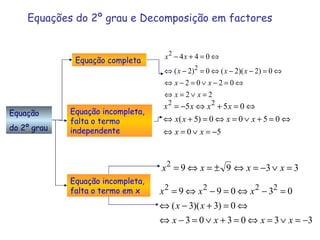
1) O documento discute equações de primeiro e segundo grau, incluindo monômios, polinômios, adição, subtração, multiplicação e divisão destes. 2) É explicado o que são equações literais e como resolver equações em ordem a uma variável específica. 3) Diferentes tipos de equações são apresentados como equações com parênteses, fracções e do segundo grau.

1. Unidade 3 Equações 8º ano Resumo Equações 8º Ano

2. Monómios e polinómios O Pedro leva na mão 1 livro e não sabe quantos livros leva na mochila. Que expressão pode representara situação? Vamos designar por n o número de livros que estão dentro da mochila. A expressão n + 1 representa a totalidade de livros que o Pedro transporta, sendo n a variável. Nesta situação podemos ter várias hipóteses, então vamos utilizar uma tabela para organizar os dados 4 3 2 1 n+1 3 2 1 0 n

3. Monómios e polinómios O que é um monómio? É uma expressão constituída por um número ou uma letra, ou por um produto de números e letra Exemplos: 3; 5n; Num monómio existe um coeficiente e uma parte literal O que é um Polinómio? É a soma de vários monómios x + 3 ; 5x +2y +3; 3x 2 + 8x + 4

4. Coeficiente parte literal e grau de um monómio Grau de um monómio é a soma dos expoentes das variáveis A Parte literal é a letra Número que está pegado à letra Não tem -5 -5 x -1/2 xy 1 xy 2 Parte literal Coeficiente Monómio 0 1 3 Grau

5. Monómios e polinómios Monómios semelhantes: têm a mesma parte literal Exemplos: 5x e 6x; 4y 2 e 6y 2 Monómios simétricos: São monómios semelhantes com coeficientes simétricos Exemplos: 5x e -5x Notas: Num monómio não há adições nem subtracções Expressão que representa a área de um triângulo b h

6. Adição de monómios e polinómios Observa a figura: as distâncias estão em metros A C B x e 2x são monómios. Nos monómios os números representam letra Se x = 4 então a distância de A até C é 4 + 2x4 = 12m Simplificação da expressão: x + 2x = 3x ( adiciona-se os coeficientes (1 + 2)) Lê-se 1 x Nota : Só se podem adicionar monómios semelhantes (com a mesma parte literal) x 2x

7. Adição de monómios e polinómios Como fazer: No problema anterior podia-se simplificar 1º a expressão: x + 2x = 3x se x = 4 então 3 x 4 = 12m Como fazer: simplifica a seguinte expressão: 1º passo – identificar os monómios semelhantes 2º passo – adicionar os monómios semelhantes x + 3y + 2 + 3x – y – 5 = = 4x + 2y -3

8. Adição de monómios e polinómios Comutativa: Propriedades Associativa : Distributiva da multiplicação em relação à adição: Elemento absorvente da Multiplicação: Elemento neutro da adição: a + b = b + a ab = ba (a + b) + c = a + (b + c) (ab)c = a(bc) a( b + c ) = ab + ac a + 0 = 0 + a = a a x 0 = 0 x a = 0

9. Simplificações de expressões com parênteses Sinal + antes do Parênteses Mantêm-se os sinais dos termos que estão dentro do parênteses Sinal - antes do Parênteses Trocam-se os sinais dos termos que estão dentro do parênteses Sinal x antes do Parênteses. Multiplica-se os termos que estão dentro do parêntese

10. Como fazer Sinal + antes do Parênteses Mantêm-se os sinais dos termos que estão dentro do parênteses 3 + ( x - 3y + 2 ) = 3 + x – 3y + 2 = x – 3y + 5 Sinal - antes do Parênteses Trocam-se os sinais dos termos que estão dentro do parênteses Sinal x antes do Parênteses. Multiplica-se os termos que estão dentro do parêntese 3 - ( x - 3y + 2 ) = 3 – x + 3y – 2 = - x + 3y + 1 3( x - 3y + 2 ) = 3x – 9y + 6

11. Produto de um monómio por um polinómio Observa a figura: Qual a área da figura? A = 2y( 3 + y) = 6y + 2y 2 Como fazer: 1) 2) 2y 3 y

12. Multiplicação de polinómios Um polinómio é a soma de vários monómios: A = ac + bc + ad + bd ( a + b ) ( c + d ) = ac + ad + bc + bd 3x 2 +21x –x -7= Qual a área da figura? ac bc ad bd Como fazer 1) 2) (3x -1 )(x + 7) = = 3x 2 + 20x -7 a b c d

13. Operações com polinómios Observa as figuras:

14. Operações com polinómios Em alguns problemas temos de efectuar operações com polinómios. Observa o seguinte exemplo : 3x + 2 Qual é o volume do cubo?

15. Quadrado do binómio Quadrado do 1º Quadrado do 2º O dobro do 1º pelo 2º ( a + b ) 2 = a 2 + 2ab + b 2 Como fazer 1) 2) 3)

16. Quantos livros são ao todo? Quantos livros existem na mochila se ao todo são 15? Expressões Equações x + 4 x + 4 = 15 Nas expressões x representa um número desconhecido. Nas equações x representa um número desconhecido mas determinado, o número 11

17. Balanças em equilíbrio

20. Resolução de Equações com parêntese Como fazer 3(x + 1) – (x -3 ) = 12  tirar os parênteses  3x + 3 – x + 3 = 12   3x – x = 12 -3 -3   2x = 6   x = 3 Passar para um membro os termos com incógnitas e para o outro os termos independentes Obter o valor da incógnita simplificar, resolvendo em ordem a x Indicar a solução

21. Equações com fracções Como fazer: Colocar com o mesmo denominador Cuidado com o sinal Indicar a solução

22. Problemas com fracções A soma de metade de um número com 2 é 3. Qual é esse número? Como Fazer Dados: seja x o número x/2 é a sua metade

23. Resolução de Problemas e equações Como fazer: x = dinheiro do Pedro x/4 = quarta parte do dinheiro que tinha = metade do restante Resolução: R: O Pedro tinha 120 euros O Pedro foi às compras. Na primeira compra gastou a quarta parte do dinheiro que tinha e na segunda compra gastou metade do restante. Verificou que lhe sobraram 45 euros. Quanto dinheiro tinha o Pedro?

24. Lei do Anulamento do Produto A lei do anulamento do produto aplica-se a equações de grau 2 ou superior Lei do anulamento do produto: Se um produto de dois factores é zero então pelo menos um dos factores é zero ab = 0  a = 0 v b =0 Como Fazer :

25. Equações do 2º grau Lei do Anulamento do Produto A figura representa um lago quadrado de área 36m2. Qual o comprimento de cada lado Resolução x? 36 m 2

26. Equações do 2º grau e Decomposição em factores Equação do 2º grau Equação completa Equação incompleta, falta o termo independente Equação incompleta, falta o termo em x

27. Equação literal Chama-se equação literal a todo as equações que têm mais de uma variável. Como resolver uma equação em ordem a uma variável Equação simplificada da velocidade de um móvel V= velocidade; e = espaço percorrido; t = tempo Resolver em ordem a e Resolver em ordem a t

28. Fim Bom trabalho Professor: Nelson Escalda