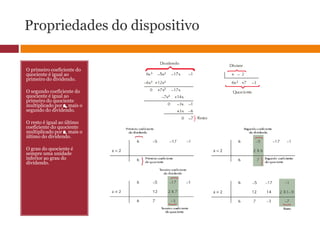
O documento discute operações com polinômios, incluindo soma, subtração, multiplicação e divisão. Ele explica como calcular o grau de um polinômio e como determinar se dois polinômios são iguais. Também apresenta o Dispositivo de Briot-Ruffini para ajudar na divisão de polinômios.

1. PolinômiosSoma de monômios

2. Polinômios Não são polinômios: Expressões com expoente fracionário e expoente negativo.Polinômio identicamente nulo:Se todos os coeficientes forem iguais a zeroGrau de um polinômio:O grau de um polinômio não nulo é o maior expoente da variável dentre os termos de coeficientes não-nulos.

3. PolinômiosValor numéricoSejam um polinômio p(x) e um número complexo α. Substituindo x pelo número α, teremos o valor numérico do polinômio para x = α.Raiz de um polinômioSe, ao substituirmos x por α, o valor numérico de um polinômio for p(α) = 0, dizemos que α é a raiz do polinômio p(x)

4. Igualdade de polinômiosDados os polinômios p(x) e q(x) na variável dizemos que eles são indenticos se, e somente se, todos os coeficientes de p(x) são, segundo suas potências, ordenadamente iguais aos de q(x).

5. Operações com polinômiosAdição e Subtração Eliminar os parênteses; Reduzir os termos semelhantes ; Ordenar de acordo com a potência ;Multiplicação Aplicar a propriedade distributiva; Reduzir os termos semelhantes.Adição (–2x² + 5x – 2) + (–3x³ + 2x – 1) = –2x² + 5x – 2 – 3x³ + 2x – 1 =–2x² + 7x – 3x³ – 3 =–3x³ – 2x² + 7x – 3Subtração (–2x² + 5x – 2) – (–3x³ + 2x – 1) =–2x² + 5x – 2 + 3x³ – 2x + 1 =–2x² + 3x – 1 + 3x³ =3x³ – 2x² + 3x – 1Multiplicação (x – 1) * (x2 + 2x - 6) x2 * (x – 1) + 2x * (x – 1) – 6 * (x – 1) =(x³ – x²) + (2x² – 2x) – (6x – 6) =x³ – x² + 2x² – 2x – 6x + 6 = x³ + x² – 8x + 6

6. Divisão – Método da chaveSendo: Verificar se A(x) e B(x) estão escritos segundo as potências decrescentes de x e se o A(x) possui termos com coeficientes iguais a 0.Dividir o 1º termo de A(x) pelo 1º termo de B(x), obtendo o 1º termo de Q(x).Multiplicar o quociente obtido por todos os termo de B(x) e colocar os resultados encontrados, com o sinal trocado, abaixo dos termos semelhantes de A(x) e efetuar a adição.Repetir o passo anterior até que o grau de R(x) seja menor que o grau de B(x).

8. (Ou Teorema do resto): O resto da divisão de um polinômio por um binômio, é igual ao valor numérico da raiz do binômio no polinômio.r(x) = p(a)RestoDivisão por polinômios do tipo x -a

9. Divisão por polinômios do tipo x - a⇒ x – b = 0 ⇒ x = b Logo, b é a raiz do binômio (divisor).Pelo teorema fundamental da divisão, temos:P(x) = (x – b). Q(x) + R(x) Substituindo b (raiz do binômio)em P(x), temos:P(b) = (b – b). Q(b) + RP(b) = (x – b). Q(b) + RP(b) = R ⇒ R= P(b) Assim:

10. Um polinômio p(x) é divisível por x – a se, e somente se, a é raiz de p(x), isto é, p(a)= 0.Teorema de D’Alembert

11. Trabalha somente com os coeficientes de um polinômio p(x) e as raízes do divisor, um binômio do tipo x-a.QuocienteDispositivo de Briot-Ruffini

12. Dispositivo de Briot-RuffiniPara lembrar: O dispositivo de Briot-Ruffini nos ajuda a achar os coeficientes do quociente e do resto quando fazemos a divisão de um polinômio por x – a.Os binômios são do seguinte tipo, por exemplo: x – 2 onde a = 2x + 3 = x – (– 3)onde a = – 3x – 1/3onde a = 1/3 Na primeira linha colocam-se os coeficientes dos termos do polinômio p(x), na ordem decrescente de seus expoentes. Se faltar algum termo, coloca-se um zero no lugar. Na terceira linha, após o traço, aparecem os coeficientes de q(x). O último número da terceira linha, situado dentro do retângulo, é o resto da divisão (R).

13. Propriedades do dispositivoO primeiro coeficiente do quociente é igual ao primeiro do dividendo. O segundo coeficiente do quociente é igual ao primeiro do quociente multiplicado por a, mais o segundo do dividendo. O resto é igual ao último coeficiente do quociente multiplicado por a, mais o último do dividendo. O grau do quociente é sempre uma unidade inferior ao grau do dividendo.

14. Dispositivo de Briot-RuffiniUma vez calculados os coeficientes do quociente, podemos escrevê-los diretamente (o grau do quociente é uma unidade inferior ao do dividendo): 6x2 + 7x – 3 O resto é o último número obtido: – 7Na divisão, quando multiplicamos um termo do quociente pelo divisor, o multiplicamos por x e por– a, mas depois mudamos seu sinal para subtraí-lo do dividendo. Por este motivo, dizemos que se multiplica por a, no Dispositivo de Briot-Ruffini. Resultado:Para lembrar: