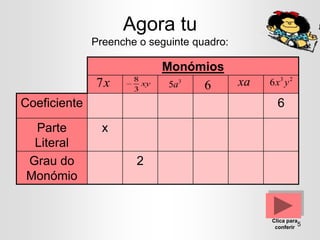
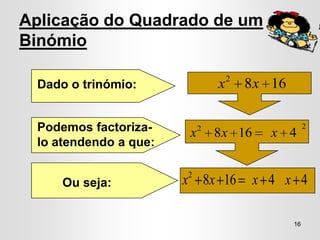
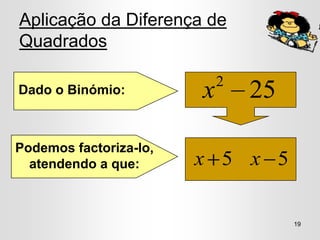
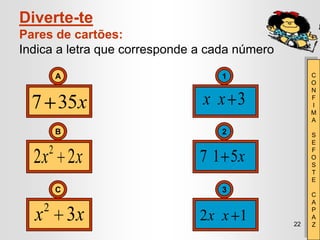
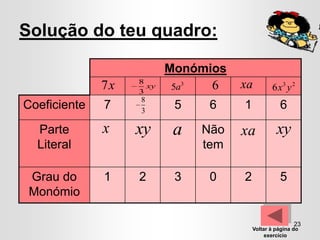
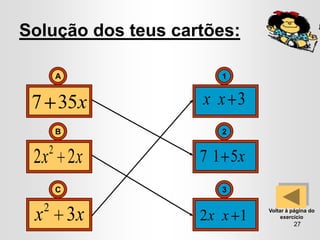
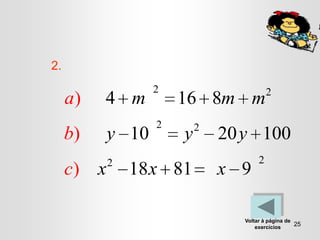O documento apresenta conceitos sobre monómios e polinómios, incluindo sua definição, composição e propriedades. É ensinada a factorização de polinómios usando propriedades como o quadrado de um binómio e a diferença de quadrados. Exercícios são fornecidos para que os alunos possam praticar estas técnicas.

1. Revisões 9º Ano

2. Monómios
• Definição
2
Um Monómio é 3x
um número ou
um produto de 8
y 6
números em que 3
7x
alguns podem ser
representados b
2
por letras. 5a
2

3. Composição de um Monómio
• Num Monómio podemos distinguir uma parte
numérica ou coeficiente e uma parte literal.
2
Monómio
5a
2
5
Coeficiente
aParte
Literal
3

4. E o grau do
Monómio o
que é???
O Grau do Monómio é
igual à soma dos
expoentes da parte literal.
4

5. Agora tu
Preenche o seguinte quadro:
Monómios
8
7x 3
xy 5a 3
6 xa 6x 3 y 2
Coeficiente 6
Parte x
Literal
Grau do 2
Monómio
Clica para
conferir
5

6. Polinómios
• Definição:
Um Polinómio é x 3
7x
a soma
algébrica de
vários monómios.
5a 2 a 4
8 1
y
3 2
3x 2 6
6

7. Composição de um Polinómio
Então,
2
no polinómio 5a a 4
às parcelas 5a ; a ; 4
2
Chamam-se termos ou monómios
7

8. Relembra que:
A+B é uma soma A X B é um produto
A e B são as parcelas A e B são os factores
8

9. Factorização de Polinómios
Definição:
Factorizar um
polinómio é escreve-lo
sob a forma de um
produto.
9

10. Aplicação:
3 x
x
A área do rectângulo da figura pode ser
dada por qualquer uma das expressões:
2
x x 3 ou x 3x
Expressão Expressão
factorizada por factorizar
10

11. Polinómios Especiais
2 3
3x x 2 x 3x 4
1 termo 2 termos 3 termos
Monómio Binómio Trinómio
11

12. Propriedade Distributiva
Para decompor um polinómio
em factores, aplicando a
propriedade distributiva,
procuramos os factores
comuns e pomos-los em
evidência.
12

13. Aplicação da propriedade distributiva
à factorização de polinómios
2
2x 8x x 2x 8
ou
2 2
2x 8x 2 x 4x
ou
2
2x 8x 2x x 4
13

14. Exercícios:
1. Decompõem num produto de factores:
a) 3x 27
b) ab b
3 2
c) 5 x 25 x 10
14
Soluções

15. Quadrado de um Binómio
Recorda que:
2 2 2
a 2ab b a b
Quadrado do Quadrado do
1º termo 2º termo
Dobro do produto
do 1º pelo 2º termo
15

16. Aplicação do Quadrado de um
Binómio
2
Dado o trinómio: x 8 x 16
Podemos factoriza- x 2
8x 16 x 4
2
lo atendendo a que:
2
Ou seja: x 8x 16 x 4 x 4
16

17. Exercícios:
2. Completa:
2
a) __ m 16 __ __
2 2
b) __ __ y __ 100
2 2
c) x __ 81 x __
17
Soluções

18. Diferença de Quadrados
Recorda que:
2 2
a b a b a b
Quadrado do 1º termo
Quadrado do 2º termo
18

19. Aplicação da Diferença de
Quadrados
2
Dado o Binómio: x 25
Podemos factoriza-lo,
atendendo a que: x 5 x 5
19

20. Exercícios:
2 2
3. Aplica a fórmula a b a b a b
para calcular cada um dos seguintes
produtos de binómios:
a) 2x 1 2x 1
2 1
b) a
16
2
c) y 25
20
Soluções

21. As igualdades:
2 2 2
a b a 2ab b
2 2
a b a b a b
São casos particulares da multiplicação
de polinómios, chamam-se por isso,
Casos Notáveis da Multiplicação.
21

22. Diverte-te
Pares de cartões:
Indica a letra que corresponde a cada número
A 1 C
O
N
7 35x x x 3 F
I
M
A
B 2 S
E
2 F
2x 2x 7 1 5x O
S
T
E
C 3
C
A
22
x x 33x
x 2x x 1 22
P
A
Z

23. Solução do teu quadro:
Monómios
8
7x 3
xy 5a3 6 xa 6x 3 y 2
8
Coeficiente 7 3
5 6 1 6
Parte x xy a Não xa xy
Literal tem
Grau do 1 2 3 0 2 5
Monómio
23
Voltar à página do
exercício

24. Soluções:
1.
a) 3 x 9
b) b a 1
3 2
c) 5 x 5x 2
Voltar à página de 24
exercícios

25. 2.
2 2
a) 4 m 16 8m m
2 2
b) y 10 y 20 y 100
2 2
c) x 18 x 81 x 9
Voltar à página de
exercícios
25

26. 3.
2
a) 4 x 1
1 1
b) a a
4 4
c) y 5 y 5
Voltar à página de 26
exercícios

27. Solução dos teus cartões:
A 1
7 35x x x 3
B 2
2
2x 2x 7 1 5x
C 3
2
x
x 2
3x
3x 2x x 1 Voltar à página do
exercício
27