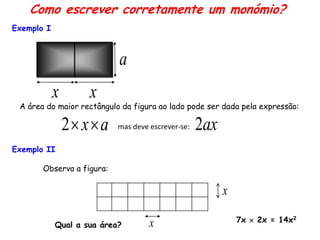
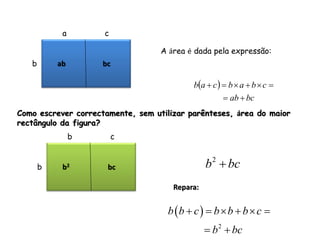
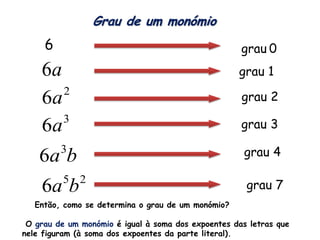
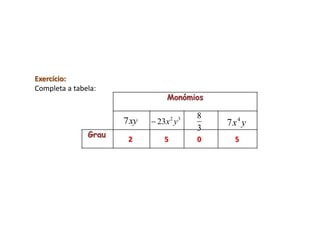
Este documento fornece informações sobre monômios e polinômios. Resume: 1. Apresenta exemplos de monômios e explica que um monômio é uma expressão algébrica constituída por um número ou produto de números e letras, podendo ter expoentes. 2. Explica que um polinômio é uma soma algébrica de dois ou mais monômios. 3. Demonstra como determinar o grau de um monômio e de um polinômio, que é igual à soma dos expoentes das letras nos

1. MONÓMIOS
E
POLINÓMIOS

2. Problema: Observa as figuras.
6
x-9 6
x–4
Sabendo que as figuras são equivalentes, determina as dimensões do rectângulo.
Resolução:
Se as figuras são equivalentes significa que têm a mesma área, logo
podemos formar a seguinte equação:
x  9x  4  36
No 1.º membro da equação surge um produto que ainda não sabem efetuar.
Portanto, torna-se necessário estudar novas expressões e suas operações
que nos permitam dar resposta a alguns problemas.

3. POLINÓMIOS
1 2a  3
 x6
2
2x2  3
7x  4
y  4y  3
2
Exemplos de várias expressões algébricas.
Uma expressão algébrica é constituída por um ou mais termos.

4. No polinómio y  4y  3
2
, às parcelas, y 2,  4 y e 3
chamam-se termos ou monómios.
Um polinómio é uma soma algébrica de pelo menos dois monómios..
Exemplos:
y2  4 y Binómio, porque é constituído por dois monómios.
4 x 2  4 x  30 Trinómios
cada expressão é constituído por 3 monómios
7 y 2  4 xy  7 xy

5. Curiosidade:
MONÓMIOS Monómio é uma palavra de
origem grega, derivada de
monos, que significa único.
Monómio significa único termo.
Um monómio é uma expressão que pode ser constituída por um
número ou por um produto de números em que alguns podem ser
representados por letras.
Exemplos:
23x
M3
y
x 
-xy 4
6
NOTA
y 1 1
  y y
4 4 4
Nota: Num monómio não aparecem adições nem subtracções.

6. Constituição de um monómio
Exemplo:
-7 y3
Neste monómio podemos distinguir uma parte numérica ou coeficiente (-7) e
uma parte literal (y3).
Exercício:
Completa a tabela seguinte:
Monómio Coeficiente Parte literal
x 1 x
 10 __
10
z 1
  z
6 6
5 yz yz 5
89xyz  89 xyz

7. Como escrever corretamente um monómio?
Exemplo I
a
x x
A área do maior rectângulo da figura ao lado pode ser dada pela expressão:
2 x  a mas deve escrever-se: 2ax
Exemplo II
Observa a figura:
x
7x  2x = 14x2
Qual a sua área? x

8. O produto de dois monómios é outro monómio cujo coeficiente é o
produto dos coeficientes e cuja parte literal é o produto das partes
literais.
Convencionou-se que para escrever um produto de vários fatores (um monómio)
escreve-se primeiro os números, e, em seguida, as letras por ordem alfabética.
Por exemplo:
Monómio Escrita correta
x 5  y 5 xy
5 b  a  3 15ab
 3  q   2 p 6 pq
3  a 2  b   2 a  b  6a3b 2

9. Grau de um monómio
6 grau 0
6a grau 1
2
6a grau 2
6a 3
grau 3
3
6a b grau 4
5 2
6a b grau 7
Então, como se determina o grau de um monómio?
O grau de um monómio é igual à soma dos expoentes das letras que
nele figuram (à soma dos expoentes da parte literal).

10. Exercício:
Completa a tabela:
Monómios
8
7 xy  23x 2 y 3 7 x4 y
3
Grau
2 5 0 5

11. Consolidação dos conhecimentos
Exercícios da página 41 (volume 2)
TPC- terminar os
exercícios não realizados
na aula e tarefa 1 da
página 38.

12. OPERAÇÕES COM
POLINÓMIOS

13. Adição algébrica de polinómios
Tal como na aritmética, também é possível simplificar expressões algébricas
quando estas têm termos semelhantes.
Aritmética Álgebra
3 + 3 + 3 + 3 = 43 a + a + a + a =4a = 4a
54 + 64 = 114 5a + 6a = 11a
37 + 27 + 47 = 97 3a + 2a + 4a = 9a
Para se obter a soma polinómios basta adicionar os termos semelhantes.

14. Exemplos: Processo:
1. O polinómio Algoritmo
6 x 4  7 x  9  4 x  6 x 4  3x  9
Polinómio reduzido porque não tem termos
semelhantes
2. Transforma num polinómio reduzido os seguintes polinómios:
6 x  7 y  9 x  4 y  12 
4 4
6 y3  2 y  5   7 y 3  y 2  3 y  10  
 15x  3 y  12
4
Simplificar um polinómio
é reduzir os termos
semelhantes

15. Consolidação dos conhecimentos
Exercícios da página 43

16. Produto de um monómio
por um polinómio

17. a c
A área é dada pela expressão:
b ab bc
ba  c   b  a  b  c 
 ab  bc
Como escrever correctamente, sem utilizar parênteses, área do maior
rectângulo da figura?
b c
b b2 bc b 2  bc
Repara:
b b  c   b  b  b  c 
 b 2  bc

18. Para multiplicar um monómio por um polinómio, aplica-se a propriedade
distributiva da multiplicação em relação à adição, isto é, multiplica-se
o monómio por cada um dos termos do polinómio.
 2 3x  3  x 1  6x  6  2 x  2

19. Monómios semelhantes
Considera o seguinte polinómio: 6x  7 x  9  4x
4
este polinómio é constituído por 4 monómios 6x 4 ,7 x ,  4 x e 9.
Os monómios
7x e  4x são semelhantes.
Mais
exemplos: 4 y 2
e 56 y 2
887xy z 2
e 4xy z
2
 4y e 19 y Conseguirás chegar à definição de monómios
semelhantes?
Monómios semelhantes - são monómios que têm a mesma parte literal.
Os monómios  4x e 6x 4 não são semelhantes porque não têm a
mesma parte literal.

20. Monómios simétricos - são monómios com a mesma parte literal e coeficientes
simétricos.
19y e 19 y
Grau de um polinómio
Consideremos o polinómios e o respetivo grau.
6 x 4  5x 2  1 O grau deste polinómio é 4
x y  x 9
5 5
Grau 6
x3  1 Grau 3
Definição:
Chama-se grau de um polinómio é o maior dos graus dos monómios que
o constituem.
x  43 x
3
grau 3 grau 1
POLINÓMIO DE GRAU 3

21. Multiplicação de polinómios

22. A figura representa um rectângulo.
x+8
x+2
A expressão que representa a sua área é:
x  8x  2 Multiplicação de dois polinómios
Para multiplicar dois polinómios também se aplica a propriedade
distributiva da multiplicação em relação à adição.

23. x  8x  2
1.º processo: 2.º processo:
x  8x  2  xx  2  8x  2 
 x 2  2 x  8 x  16 
 x 2  10 x  16
x  8x  2  x  2x  8x  16 
2
x  10 x  16
2  x  10 x  16
2
Polinómio reduzido Para multiplicar polinómios, multiplica-se
cada termo de um, por todos os termos do
outro, obtendo-se assim um novo polinómio.
Expressão que representa a área
do rectângulo dado. 3.º processo:
Algoritmo

24. Exercício:
Transforma num polinómio reduzido:
3x  2 x  5 Se tivermos dois polínómios de graus 2 e 4
então a multiplicação desses polínómios
dará um polinómio de grau 6
 1
 y   2 x  6
 2
  
2 x 2  3x 4  10 x3 
2
2
1   1 
 y   10 0,4 y  y 2 
3   3 
 2 1  x 
 x  2 x     1
 4  2 
x  53x  1  2x2  3

25. OBSERVAÇÃO:
 3x 2
 2   x  5  3x  15x  2 x  10
4 6 2 4
Polinómio de grau 2
Polinómio de grau 4 Polinómio de grau 6
A multiplicação de um polinómio de grau 2 por um polinómio de grau 4 é um polinómio
de grau 6.
grau  P  Q   grau  P   grau Q 
 1
 y   2 x  6
 2

26. Consolidação dos conhecimentos
Exercícios da página 47 e 49
TPC- terminar os
exercícios não realizados
na aula