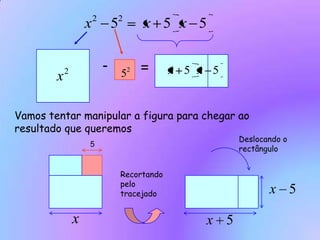
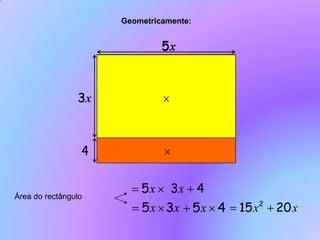
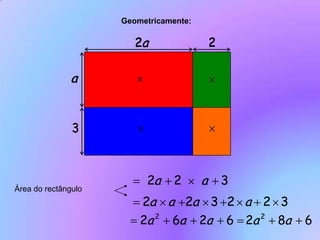
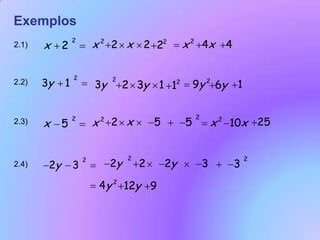Este documento discute vários tópicos sobre multiplicação de monômios e polinômios, incluindo a fórmula do quadrado de um binômio. A fórmula é derivada geometricamente como a área de um quadrado e algebricamente através da propriedade distributiva. Exemplos e exercícios são fornecidos para praticar a aplicação da fórmula. A diferença de quadrados simétricos também é discutida geometricamente como áreas de figuras sobrepostas.

1. Multiplicação deMonómios e Polinómios

2. Multiplicação de Monómios

3. O Quadrado de um MonómioOU

4. Multiplicação de um Monómiopor um Polinómio

5. Geometricamente:Área do rectângulo

6. Multiplicação de Polinómios

7. Geometricamente:Área do rectângulo

8. Casos Notáveis da Multiplicação

9. Quadrado do binómioJá vimos quepode ser visto como o produto de 2 polinómios, então:Temos 2 termos semelhantes que podemos simplificar

10. GeometricamenteEste quadrado de um binómio pode ser visto como a área de um quadrado de lado Decompondo a figura a área é igual à soma das áreas de cada uma das figuras

11. PraticandoTenta descobrir uma lei que te permita escrever directamente o quadrado de um binómio!

12. 1) Observa a figura1.1) Qual é a medida do comprimento do lado do quadrado [ABCD]?a + bA medida do lado é

13. 1.2) E qual é a sua área?A área é (a+b)(a+b)=(a+b)²1.3) Recorta a figura pelo tracejado. Qual é a área de cada uma das figuras obtidas? As figuras obtidas são dois quadrados de áreas a² e b² e dois rectângulos de área ab.

14. 1.4) Estes quatro quadriláteros obtidos têm origem no quadrado original. Portanto a área do quadrado original é igual à soma das áreas destes quatro quadriláteros, ou seja, ou ainda, Esta fórmula é conhecida porFórmula do Quadrado do BinómioEsta fórmula é um Caso Notável da Multiplicação

15. 1.5) Vejamos o que acontece algebricamente. Sabemos que Então, aplicando a propriedade distributiva, duas vezes, obtemos Resulta daqui que: Esta fórmula é conhecida porFórmula do Quadrado do Binómio

16. De um modo geralRepara que:Quadrado do 2.º termoDobro do produto do 1.º termo pelo 2.º termoQuadrado de um binómio:a é o 1.º termo do binómiob é o 2.º termo do binómioQuadrado do 1.º termo

17. Exemplos2.1) 2.2) 2.3) 2.4)

18. Exercícios3.1) 3.2) 3.3) 3.4)

19. Diferença de quadradossimétricosO termo 25 pode ser escrito como um quadrado

20. GeometricamenteQueremos mostrar que:Pode ser visto como a área de um rectângulo de ladosPode ser visto como a área de um quadrado de lado 5Pode ser visto como a área de um quadrado de lado

21. -=Vamos tentar manipular a figura para chegar ao resultado que queremosDeslocando o rectângulo 5Recortando pelo tracejado

22. De um modo geralRepara que:Quadrado do 1.º termoQuadrado do 2.º termo1º 2º 1º 2º

23. ConclusõesO produto de dois binómios que só diferem no sinal de um dos termos é igual à diferença dos quadrados dos termos. O sinal -, da diferença, fica associado ao quadrado do termo que tem sinal diferente. Exemplo:

24. Praticando