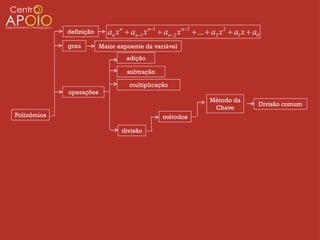
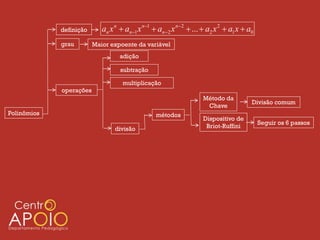
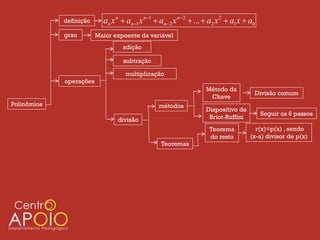
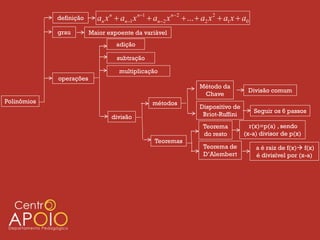
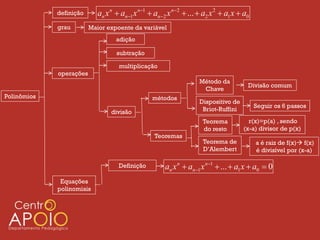
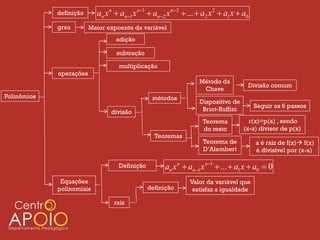
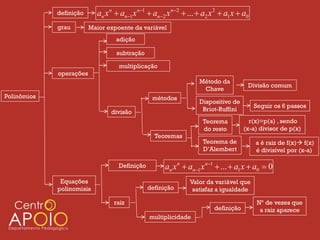
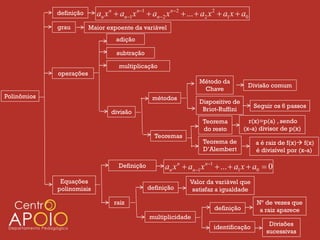
O documento apresenta uma introdução sobre polinômios, definindo-os como expressões algébricas na forma anxn + an-1xn-1 + ... + a2x2 + a1x + a0, onde an, ..., a0 são coeficientes e n é o grau do polinômio. Em seguida, aborda operações com polinômios como adição, subtração e multiplicação, além de métodos de divisão como o da chave.