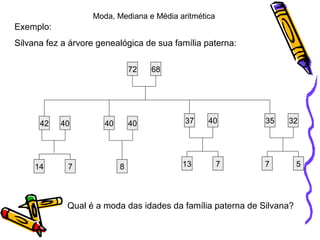
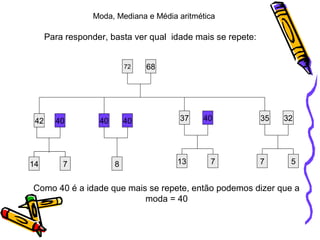
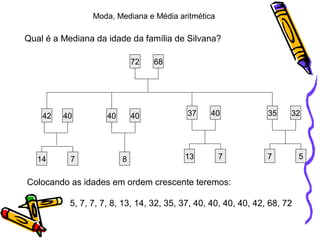
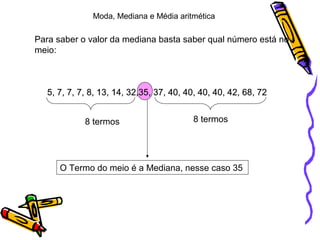
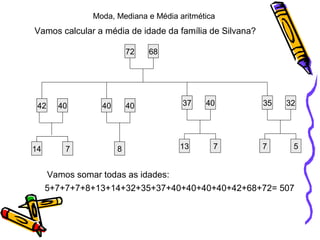
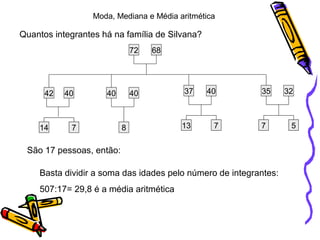
O documento explica os conceitos de moda, mediana e média aritmética em uma família. A moda é a idade que mais se repete, que é 40 anos. A mediana é o valor do meio quando as idades são ordenadas, que é 35 anos. A média aritmética é obtida dividindo a soma das idades pelo número total de pessoas, que é 29,8 anos.

1. Moda, Mediana e Média Aritmética
Juliana Perleto Rodrigues

2. Moda, Mediana e Média aritmética
Moda de um conjunto de valores é o elemento que ocorre mais
frequentemente dentro desse conjunto.
O que é Moda?

3. Exemplo:
Silvana fez a árvore genealógica de sua família paterna:
72 68
42 40 40 40 37 40 35 32
14 7 8 13 7 7 5
Qual é a moda das idades da família paterna de Silvana?
Moda, Mediana e Média aritmética

4. Para responder, basta ver qual idade mais se repete:
72 68
42 40 40 40 37 40 35 32
14 7 8 13 7 7 5
Como 40 é a idade que mais se repete, então podemos dizer que a
moda = 40
Moda, Mediana e Média aritmética

5. O que é Mediana?
Mediana de um conjunto finito de valores, dispostos em ordem
crescente ou decrescente de grandeza, é o valor central, se o
conjunto tiver um número ímpar de elementos, ou é a média aritmética
dos dois valores centrais, se o conjunto tiver um número par de
elementos.
Moda, Mediana e Média aritmética

6. Qual é a Mediana da idade da família de Silvana?
72 68
42 40 40 40 37 40 35 32
14 7 8 13 7 7 5
Colocando as idades em ordem crescente teremos:
5, 7, 7, 7, 8, 13, 14, 32, 35, 37, 40, 40, 40, 40, 42, 68, 72
Moda, Mediana e Média aritmética

7. Para saber o valor da mediana basta saber qual número está no
meio:
5, 7, 7, 7, 8, 13, 14, 32,35, 37, 40, 40, 40, 40, 42, 68, 72
8 termos 8 termos
O Termo do meio é a Mediana, nesse caso 35
Moda, Mediana e Média aritmética
5, 7, 7, 7, 8, 13, 14, 32,35, 37, 40, 40, 40, 40, 42, 68, 725, 7, 7, 7, 8, 13, 14, 32,35, 37, 40, 40, 40, 40, 42, 68, 725, 7, 7, 7, 8, 13, 14, 32,35, 37, 40, 40, 40, 40, 42, 68, 72

8. O que é Média Aritmética?
Média Aritmética de um conjunto de números é o valor que se obtém
dividindo a soma dos seus elementos pelo número de elementos do
conjunto.
Moda, Mediana e Média aritmética

9. Vamos calcular a média de idade da família de Silvana?
72 68
42 40 40 40 37 40 35 32
14 7 8 13 7 7 5
Vamos somar todas as idades:
5+7+7+7+8+13+14+32+35+37+40+40+40+40+42+68+72= 507
Moda, Mediana e Média aritmética

10. Quantos integrantes há na família de Silvana?
72 68
42 40 40 40 37 40 35 32
14 7 8 13 7 7 5
São 17 pessoas, então:
Basta dividir a soma das idades pelo número de integrantes:
507:17= 29,8 é a média aritmética
Moda, Mediana e Média aritmética