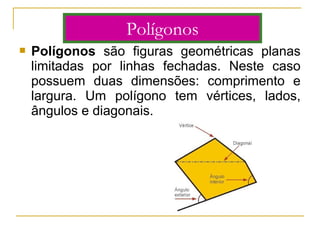
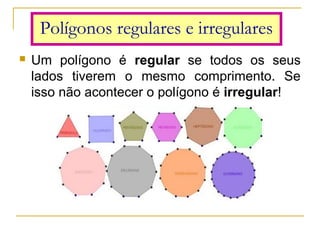
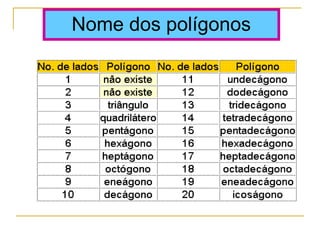
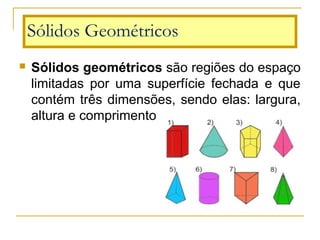
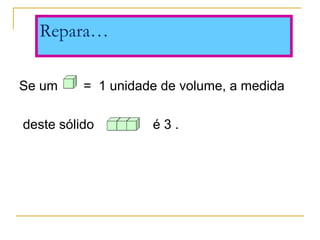
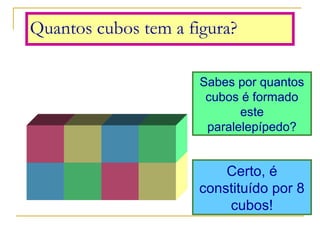
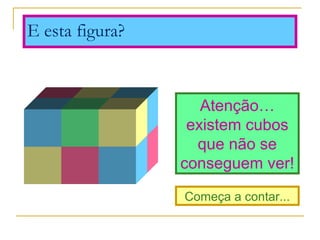
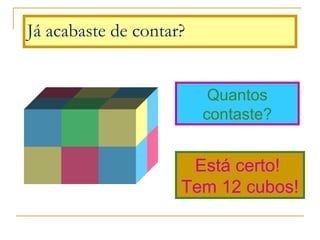
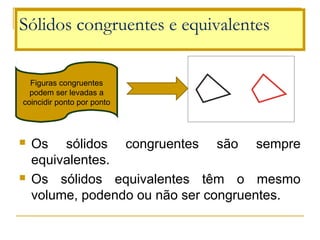
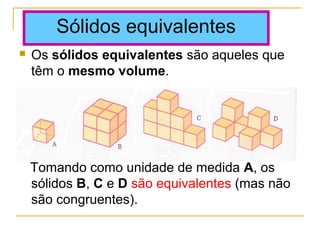
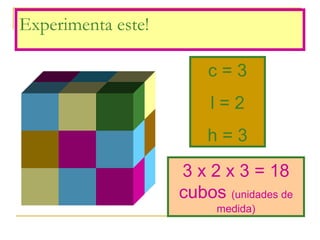
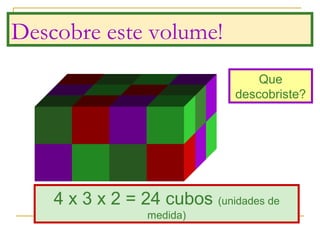
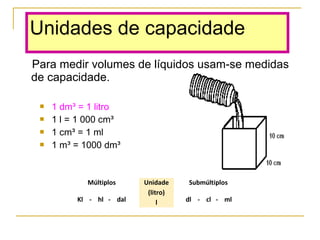
O documento discute polígonos, sólidos geométricos e volume. Polígonos são figuras planas com lados e ângulos, enquanto sólidos geométricos têm três dimensões. O volume é a quantidade de espaço ocupada e é calculado multiplicando comprimento, largura e altura para paralelepípedos ou aresta ao cubo para cubos.

1. Volumes - 6º ano
Matemática

2.  Polígonos são figuras geométricas planas
limitadas por linhas fechadas. Neste caso
possuem duas dimensões: comprimento e
largura. Um polígono tem vértices, lados,
ângulos e diagonais.
Polígonos

3.  Um polígono é regular se todos os seus
lados tiverem o mesmo comprimento. Se
isso não acontecer o polígono é irregular!
Polígonos regulares e irregulares

4. Nome dos polígonos

5.  Sólidos geométricos são regiões do espaço
limitadas por uma superfície fechada e que
contém três dimensões, sendo elas: largura,
altura e comprimento.
Sólidos Geométricos

7.  O volume de um corpo é a quantidade de
espaço que ele ocupa.
 Para medir o volume de um sólido é
necessário definir a porção de espaço que
corresponde a uma unidade de medida.
Depois, o volume do sólido é igual ao
número de vezes que a unidade de medida
cabe no sólido ou em quantas dessas
unidades o sólido se pode decompor.
Volume

8. Se um = 1 unidade de volume, a medida
deste sólido é 3 .
Repara…

9. Quantos cubos tem a figura?
Sabes por quantos
cubos é formado
este
paralelepípedo?
Certo, é
constituído por 8
cubos!

10. E esta figura?
Atenção…
existem cubos
que não se
conseguem ver!
Começa a contar...

11. Já acabaste de contar?
Quantos
contaste?
Está certo!
Tem 12 cubos!

12.  Os sólidos congruentes são sempre
equivalentes.
 Os sólidos equivalentes têm o mesmo
volume, podendo ou não ser congruentes.
Sólidos congruentes e equivalentes
Figuras congruentes
podem ser levadas a
coincidir ponto por ponto

13.  Os sólidos equivalentes são aqueles que
têm o mesmo volume.
Tomando como unidade de medida A, os
sólidos B, C e D são equivalentes (mas não
são congruentes).
Sólidos equivalentes

14. Qual será a fórmula para o cálculo de
volumes ?

15. Volume do paralelepípedo retângulo
 Vamos considerar o paralelepípedo rectângulo da
figura, no qual:
h
l
c
ac= comprimento
l = largura
h = altura
De modo prático, obtemos o volume do
paralelepípedo multiplicando comprimento,
largura e altura, ou seja, V = c x l x h

16. Experimenta este!
c = 3
l = 2
h = 3
3 x 2 x 3 = 18
cubos (unidades de
medida)

17. Descobre este volume!
Que
descobriste?
4 x 3 x 2 = 24 cubos (unidades de
medida)

18.  A unidade usada para se medir volume é o metro cúbico ( m³ ).
 1 m³ é o volume ocupado por um cubo de 1 metro de aresta.
 Cada unidade é 1000 vezes maior que a unidade
imediatamente inferior.
Unidades de medida de volumes
Múltiplos
Km3
I hm3
I dam3
Unidade
m3
Submúltiplos
dm3
I cm3
I mm3

19. Para medir volumes de líquidos usam-se medidas
de capacidade.
 1 dm³ = 1 litro
 1 l = 1 000 cm³
 1 cm³ = 1 ml
 1 m³ = 1000 dm³
Unidades de capacidade
Múltiplos
Kl - hl - dal
Unidade
(litro)
l
Submúltiplos
dl - cl - ml

20. EXERCÍCIOS
 1. Faz as transformações:
a) 2,5 dm³ = litros
b) 3,2 ml³ = cm³
c) 0,7 m³ = dm³
d) 7,5 cm³ = litros
e) 290 cl = ml
f) 3 litros = dm³ = cm³
0,0032
2,5
700
0,0075
2900
3 0003

21. Problema
2. Uma caixa de chocolates tem a forma de
um paralelepípedo rectângulo, com as
seguintes medidas : 4m altura , 3m
comprimento e 1,5m largura. Qual o volume
dessa caixa?
V = 4m x 3m x 1,5m
V = 18 m³

22. VOLUME DO CUBO
 Calcular o volume de um cubo necessitamos
da seguinte fórmula:
a
a
a V = a x a x a
V= aresta x aresta x aresta

23. EXERCÍCIOS
 Quero construir uma piscina de 5m de comprimento
por 5m de largura e 5m de profundidade. Qual o
volume de terra que deve ser retirado?
V= a x a x a
V= 5m x 5m x 5m
V= 125m3