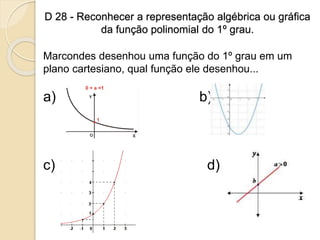
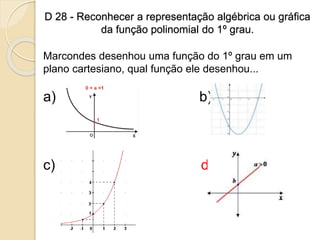
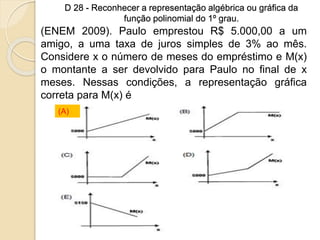
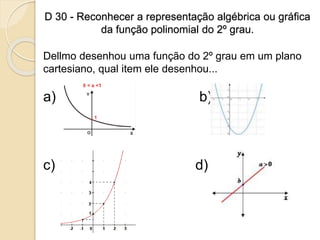
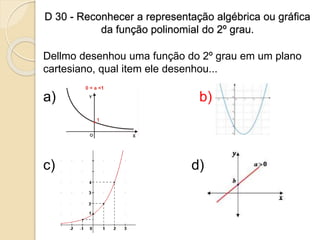
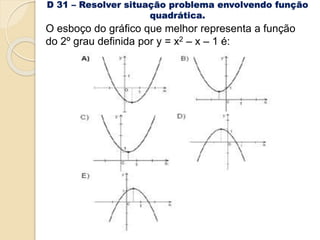
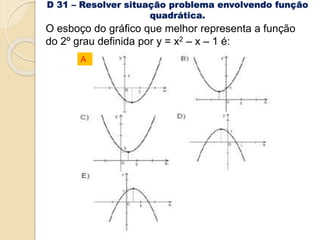
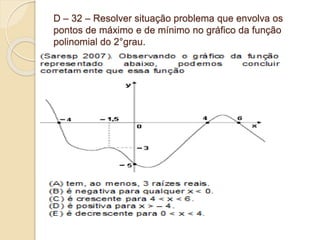
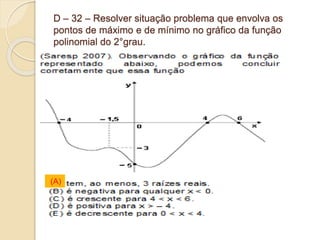
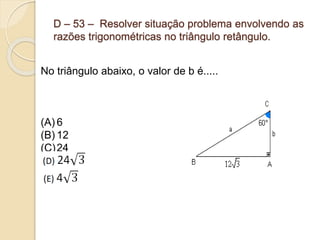
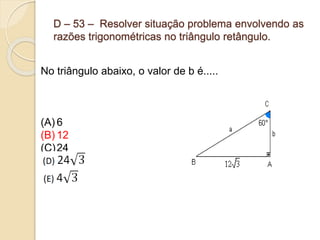
1) O documento apresenta descritores de matemática relacionados a funções polinomiais do 1o e 2o grau. 2) São fornecidos exemplos de situações-problema envolvendo reconhecimento, representação e resolução de funções polinomiais. 3) Também são abordados conceitos como progressões aritméticas e geométricas.