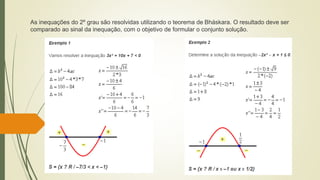
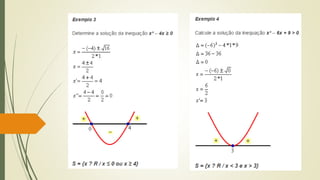
1) O documento discute inequações do segundo grau, explicando que assim como equações, devem seguir os mesmos passos para resolução, porém o conjunto solução é diferente. 2) Apresenta um exemplo numérico de resolução de uma inequação do primeiro grau para ilustrar os conceitos. 3) Explica que para inequações do segundo grau, deve-se utilizar o Teorema de Bhaskara para encontrar os valores de x, e comparar ao sinal da inequação original para definir o conjunto solução.

1. Inequações do 2° Grau
Inequação é uma expressão matemática
que possui a propriedade de expressar
desigualdades.
A principal diferença de uma Equação é
que não tem o sinal de igual .
Na inequação usaremos os seguintes símbolos
matemáticos no lugar do igual das Equações:
> : maior que
< : menor que
≥ : maior que ou igual
≤ : menor que ou igual

2. Para resolver uma inequação segue-se os mesmos passos que na
resolução de uma equação.
O que irá diferenciar da equação será o conjunto solução.
Exemplo: Considerando o conjunto dos nºs Reais, resolva a inequação:
2x + 7 > –1 + 2
2x > –1 + 2 – 7
2x > –8+2
2x > –6
x > –3
Conjunto Solução: {xЄR/x > –3}
Lendo a solução: x pertence aos Reais tal que x é maior que -3
Є = pertence R = conjunto dos números Reais / = tal que

3. Conjunto Universo :
É o conjunto de todos os valores que
variável pode assumir.
Indica-se por U.
Exemplo na inequação:
2x + 7 > –1 + 2
O Conjunto Universo é formado por todos
os valores maiores que -3, ou seja:
(-2,-1,0,1,2,3,...)

4. Outro exemplo:
Considerando como universo o conjunto
dos números naturais,
determine o conjunto solução da inequação:
5x – 8 < 3x + 12
5x – 3x < 12 + 8
2x < 20
x < 20/2
x < 10
Assim o conjunto solução da inequação é:
S = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

5. 3 2x  
3 2x   
2
3
x  
Equação: Inequação:
Quando numa inequação é necessário multiplicar ou dividir os dois membros
por um número negativo inverte-se o sinal da desigualdade.
Resolve-se uma inequação do mesmo modo que uma equação.
2
3
S
 
  
 
3 2x  
3 2x   
2
3
x  
2
,
3
S
 
    
Ao multiplicar os
dois membros por
-1 inverte-se o
sinal da
desigualdade

6. Para resolver inequações do segundo grau, precisamos, antes, recordar que as inequações de primeiro
grau são resolvidas seguindo-se o mesmo procedimento utilizado na resolução das equações de primeiro
grau e observando-se, claro, as propriedades das desigualdades e o significado da solução.

7. É possível, para resolver
inequações do segundo grau,
proceder como em equações
do segundo grau?

8. E agora? Qual seria o significado dos valores encontrados para o conjunto solução? Se a inequação é
x² - 3x - 4 > 0, deveríamos escrever a solução como x > 4 ou x > -1? Que significado isso teria?
Na verdade, resolver a inequação x² - 3x - 4 > 0 é saber para quais valores de x a expressão x² - 3x - 4
é positiva.
Graficamente, essa expressão, em função de x, é uma parábola, uma função do 2° grau. Estudando o
sinal da função do 2° grau, descobre-se para quais valores de x essa expressão é positiva.
Seu gráfico é:

9. Estudando o sinal da função, temos
Logo, os valores de x que fazem com que a expressão
seja positiva são x > -1 ou x > 4. E o conjunto solução da
inequação é S={xE R/ x < -1 ou x >4}

11. As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser
comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.