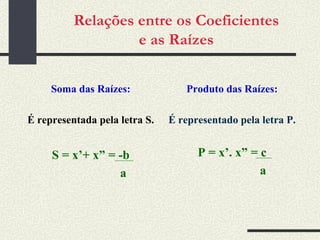
O documento apresenta conceitos sobre equações do segundo grau, incluindo definição, tipos de equações (completas e incompletas), resolução utilizando a fórmula de Bhaskara e discriminante, e relações entre coeficientes e raízes. Há também exemplos de resolução de equações.

1. MATEMÁTICA 6º AO 9º ANO E. M. PROFª IRACEMA DE SOUZA MENDONÇA SALA DE INFORMÁTICA - MATUTINO

2. ESCOLA M PROFª IRACEMA DE S. MENDONÇA ALUNO(A): ALUNO(A): ANO: DATA: PROFESSORA: MARIA LUCIA PCTE: ROSENY LEIA COM MUITA ATENÇÃO CADA INFORMAÇÃO CONTIDA EM CADA SLIDE, PARA RESOLVER OS EXERCÍCIOS COM MUITA SEGURANÇA. Dara Alessandra Elis Regina 9ano A 27/05/2011

3. Equações do 2º Grau ax 2 + bx + c = 0, a ≠ 0

4. Definição: Denomina-se equação do 2º grau, na incógnita x , toda equação da forma: ax 2 + bx + c = 0, a ≠ 0. Observe que: a representa o coeficiente de x²; b representa o coeficiente de x; c representa o termo independente. Exemplos: x 2 - 5x + 6 = 0 , onde a = 1, b = -5 e c = 6.  7x 2 - x = 0 , onde a = 7, b = -1 e c = 0. x 2 - 36 = 0 , onde a = 1, b = 0 e c = -36.

5. Equações Completas do 2º Grau Uma equação do 2º grau é completa quando b e c são diferentes de zero. Exemplos: x² - 9x + 20 = 0 , onde a = 1, b = -9 e c = 20. -x² + 10x - 16 = 0 , onde a = -1, b = 10 e c = -16.

6. Equações Incompletas do 2º Grau Uma equação do 2º grau é incompleta quando b ou c é igual a zero, ou ainda, quando ambos são iguais a zero. Equações da forma ax² +bx = 0, (c = 0)  x² - 3x = 0 , onde a = 1, b = -3.  -2x² + 4x = 0 , onde a = -2, b = 4. Equações da forma ax² +c = 0, (b = 0) 3x² - 2 = 0 , onde a = 3, c = -2. x² + 5 = 0 , onde a = 1, c = 5.

7. ATIVIDADE-1 1. Obtenha os coeficientes das equações do 2° grau: a) 5x²-7x-3=0 a:5 b:-7 c:-3 b) x²-4x +2=0 a:1 b:-4 c:2 c) x²-x-1=0 a:1 b:-1 c:-1 d) 2x²+7x+8=0 a:2 b:7 c:8 e) x²-7x=0 a:1 b:-7 c:0 f) x²-25=0 a:1 b:0 c:-25

8. 2. Forme as equações do 2° grau em x: a=1; b=-6 ; c= 5 x²-6x+5=0 b) a=3; b=7 ; c= 8 3x²+7x+8=0 c) a=8; b=0 ; c=0 8x²=0 d) a=1; b=-3 ; c= 4 x²-3x+4=0 e) a=7; b=1 ; c= -15 7x²+1x-15=0

9. Raízes de uma Equação do 2º Grau Resolver uma equação do 2º grau significa determinar suas raízes . Raiz é o número real que, ao substituir a incógnita de uma equação, transforma-a numa sentença verdadeira. O conjunto formado pelas raízes de uma equação denomina-se conjunto verdade ou conjunto solução .

10. Resolver uma equação significa determinar o seu conjunto verdade . Utilizamos na resolução de uma equação incompleta as técnicas da fatoração e duas importantes propriedades dos números reais : 1ª Propriedade: Se x є IR , y є IR e x.y = 0 x = 0 ou y = 0 2ª Propriedade: Se x є IR , y є IR e x² = y x = √ y ou x = - √y 1º Caso: Equações da forma ax² +bx = 0, (c = 0) 2º Caso: Equações da forma ax² +c = 0, (b = 0) Resolução de Equações Incompletas

11. Resolução de Equações Incompletas Equações da forma: ax² +bx = 0, (c = 0) De modo geral, a equação do tipo ax² +bx = 0 tem para soluções: x = 0 e x = - b a Equações da forma: ax² +c = 0, (b = 0) De modo geral, a equação do tipo ax² +c = 0:  possui duas raízes reais se: - c for um nº positivo a não possui raiz real se: - c for um nº negativo a

12. ATIVIDADE-2 1.Determine o conjunto verdade das equações: x²-7x = 0 Δ=b²-4.a.c x=7+7=14/2=7 Δ=7²-4.1.0 x=7-7=0/2=0 Δ=49 b) 3x²-6x = 0 Δ=b²-4.a.c x=6+6=12/6=2 Δ=-6²-4.3.0 x=6-6=0/2=0 Δ=36 c) x² +5x = 0 Δ=b²-4.a.c x=-5+5=0/2=0 Δ=5²-4.1.0 x=-5-5=-10/2=-5 Δ=25

13. 2.Determine o conjunto verdade das equações: X² - 49 = 0 a=1 Δ=0²-4.1.49 x=14/2=7 Δ=196 2x² -32 = 0 Δ=0²-4.2.32 x=16/4 =4 Δ= 0+256 Δ=256 5x² - 20 = 0 Δ=0²-4.5.-20 Δ=400 x= 0+20=20/10=5

14. Resolução de Equações Completas Fórmula de Bhaskara Para solucionar equações completas do 2º grau utilizaremos a Fórmula de Bhaskara . A partir da equação ax 2 + bx + c = 0 , a ≠ 0, desenvolveremos passo a passo a dedução da Fórmula de Bhaskara . 1º passo: multiplicaremos ambos os membros por 4a. (4a).(ax² + bx + c) = 0.(4a) 4a²x² + 4abx + 4ac = 0 2º passo: passar 4ac para o 2º membro. 4a²x² + 4abx = - 4ac

15. Fórmula de Bhaskara 3º passo: adicionar b² aos dois membros . 4a²x² + 4abx + b² = b² - 4ac 4º passo: fatorar o 1º elemento . (2ax + b) ² = b² - 4ac 5º passo: extrair a raiz quadrada dos dois membros . √ (2ax + b) ² = ± √ b² - 4ac 2ax + b = ± √ b² - 4ac 6º passo: passar b para o 2º membro . 2ax = - b ± √ b² - 4ac Trinômio Quadrado Perfeito

16. Fórmula de Bhaskara 7º passo: dividir os dois membros por 2a. 2ax = - b ± √ b² - 4ac 2a 2a Assim, encontramos a fórmula resolutiva da equação do 2º grau: x = - b ± √ b² - 4ac 2a Podemos representar as duas raízes reais por x' e x", assim: x’ = - b + √ b² - 4ac e x” = - b - √ b² - 4ac 2a 2a

17. Discriminante Denominamos discriminante o radical b 2 - 4ac que é representado pela letra grega Δ (delta). Δ = b 2 - 4ac Podemos agora escrever deste modo a Fórmula de Bhaskara: x = - b ± √ Δ 2a De acordo com o discriminante, temos três casos a considerar: 1º Caso: O discriminante é positivo (Δ > O) 2º Caso: O discriminante é nulo (Δ = O) 3º Caso: O discriminante é negativo (Δ < O)

18. Discriminante Δ > O Δ = O Δ < O O valor de √ Δ é real e a equação tem duas raízes reais diferentes, assim representadas: O valor de √ Δ é nulo e a equação tem duas raízes reais e iguais, assim representadas: O valor de √ Δ não existe em IR , não existindo, portanto, raízes reais. x’ = - b + √ Δ 2a x” = - b - √ Δ 2a x’ = x” = -b 2a As raízes da equação são número complexos .

19. Equações Fracionárias Redutíveis a Equações do 2º Grau Nessas equações (há incógnita no denominador), devemos garantir que nenhum dos denominadores se anule. Vejamos, através do exemplo a seguir, como se resolvem as equações fracionárias.  x + 1 = 5 (x ≠ 3) x - 3 - O m.m.c. é x – 3: x. (x – 3) + 1 = 5. (x – 3) x – 3 x – 3 x – 3 - Eliminando os denominadores: x. (x – 3) + 1 = 5. (x – 3) x² – 3x + 1 = 5x – 15

20. Equações Fracionárias Redutíveis a Equações do 2º Grau - Transpondo e reduzindo: x² – 3x – 5x + 1 + 15 = 0 x² – 8x + 16 = 0 - Temos: Δ = b 2 - 4ac a = 1 Δ = (-8)² - 4 . 1 . 16 b = -8 Δ = 64 - 64 c = 16 Δ = 0 - Substituindo na fórmula: x = - b ± √ Δ 2a x = - (-8) ± 0 = 8 ± 0 x’ = x” = 4 2 . 1 2 Logo, V = {4}

21. x² -7x + 6 = 0 Temos: Δ = b 2 – 4.a.c a =1 Δ =b²-4.a.c b = -7 Δ =7²-4.1.6 c = 6 Δ = 49-24=25 Substituindo na fórmula: x = - b ± √ Δ 2a X=7+5=12/2=6 x=7-5=2/2=1 ATIVIDADE- 3 Resolva as equações do 2º grau.

22. b) -x² +12x - 20 = 0 Temos: Δ = b² – 4.a.c a = -1 Δ =12²-4.-1.-20 b = 12 Δ = 144-80 c =-20 Δ = 81 Substituindo na fórmula: x = - b ± √Δ 2.a x=-12+9=3/2 x=-12-9=11/2 2. Resolva as equações do 2º grau.

23. Relações entre os Coeficientes e as Raízes 1ª Relação: Soma das Raízes ( S ) x’+x” = - b + √ Δ + - b - √ Δ = - b + √ Δ - b - √ Δ = -2b = -b 2a 2a 2a 2a a 2ª Relação: Produto das Raízes ( P ) x’.x” = -b+√ Δ . -b-√ Δ = ( -b+√ Δ) . (-b-√ Δ) = (-b)²-( √ Δ)² = b ² -Δ 2a 2a 4a ² 4a ² 4a ² Como ∆ = b² - 4ac , temos: x’.x” = b ² - (b ² - 4.a.c) = b ² - b ² + 4.a.c = 4.a.c = c 4a ² 4a ² 4.a.a a

24. Relações entre os Coeficientes e as Raízes Soma das Raízes: É representada pela letra S. S = x’+ x” = -b a Produto das Raízes: É representado pela letra P. P = x’. x” = c a

25. Composição de uma Equação do 2º Grau, Conhecidas as Raízes Considere a equação do 2º grau ax 2 + bx + c = 0. Dividindo todos os termos por a , a ≠ 0, obtemos: ax 2 + bx + c = 0 x 2 + bx + c = 0 a a a a a Como: S = x’+ x” = -b e P = x’. x” = c a a Podemos escrever a equação desta maneira: x 2 - Sx + P = 0

26. Exercício sobre Composição Componha a equação do 2º grau cujas raízes são -2 e 7. Solução: A soma das raízes corresponde a: S = x 1 + x 2 = -2 + 7 = 5 O produto das raízes corresponde a: P = x 1 . x 2 = ( -2) . 7 = -14 A equação é dada por x 2 - Sx + P = 0 , onde S = 5 e P = -14. Logo, x 2 - 5x - 14 = 0 é a equação procurada.

27. Componha a equação do 2º grau cujas raízes são: 5 e 2 -2 e -3 x²-sx+p=0 x²+5x-6=0 4 e -5 x²-sx+p=0 x²+1x+20=0 -5 e 5 x²-sx+p=0 x²-25=0 ATIVIDADE – 4 x²-sx+p=0 x²-7x+10=0