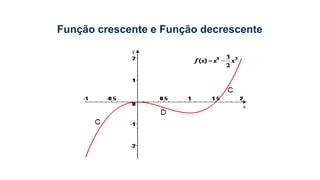
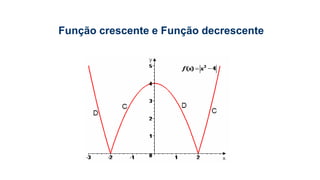
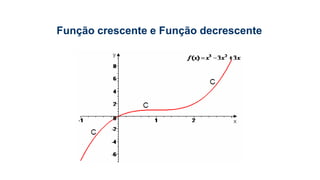
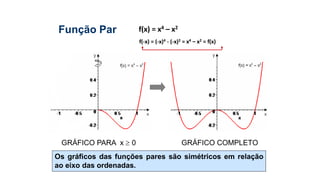
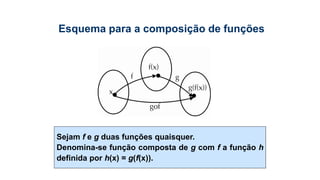
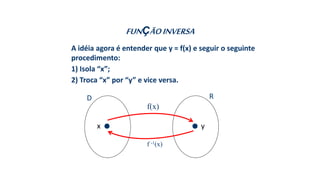
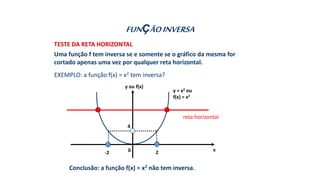
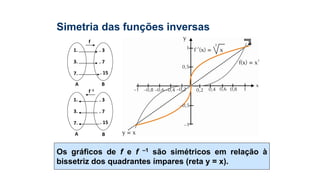
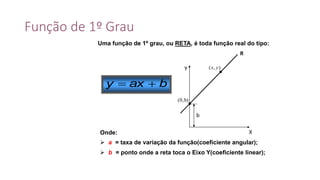
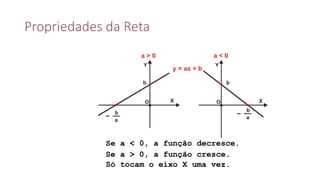
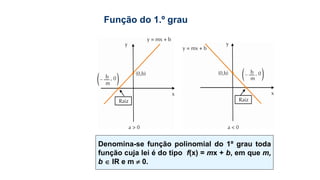
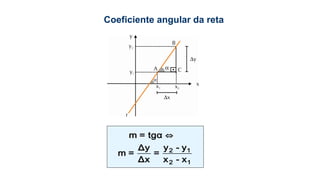
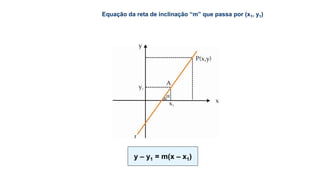
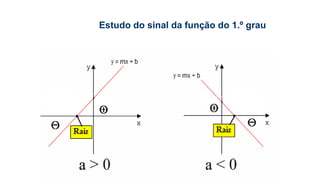
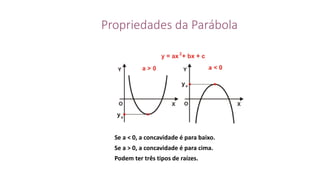
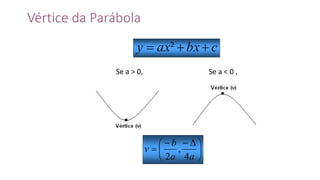
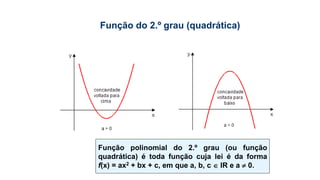
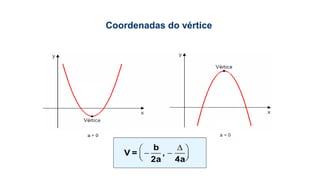
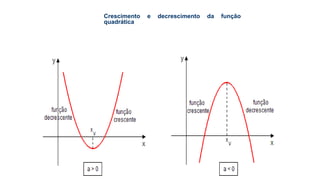
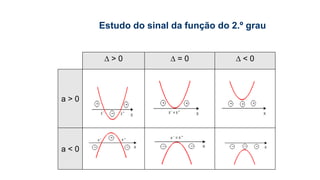
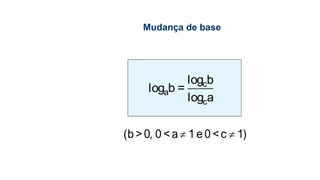
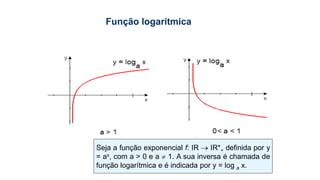
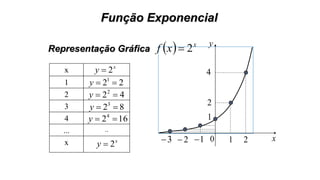
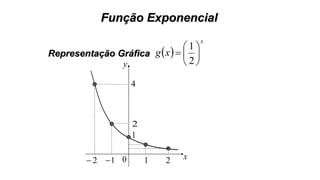
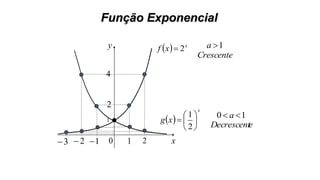
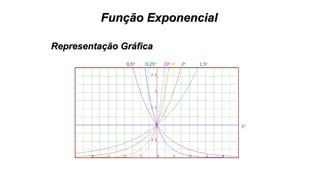
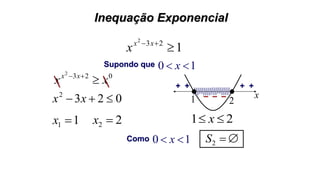
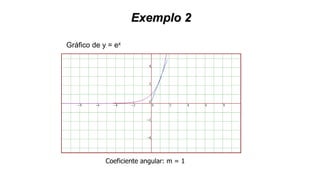
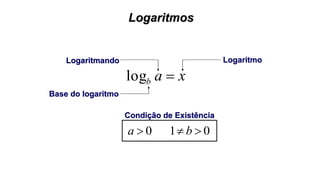
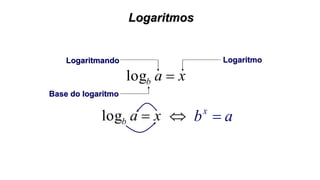
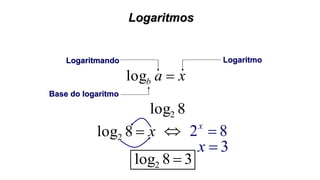
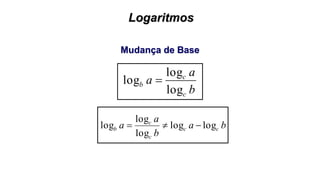
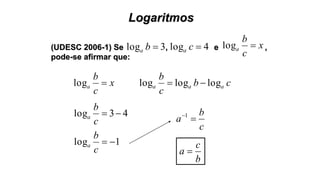
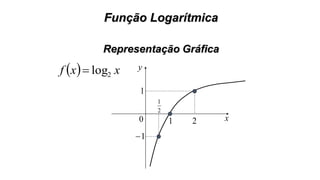
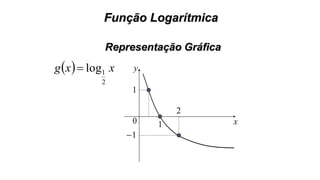
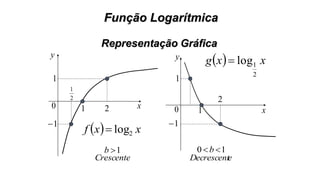
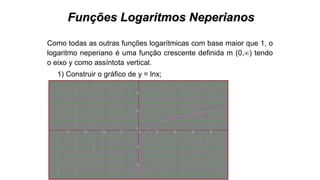
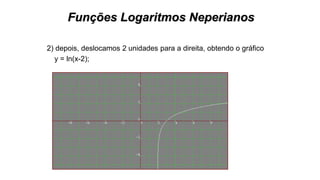
Este documento fornece informações sobre fatoração de polinômios e resolução de equações de primeiro e segundo grau. Apresenta exemplos de fatoração por evidência, agrupamento, diferença de quadrados e trinômio perfeito. Explica também o teorema do resto de um polinômio e métodos de resolução de equações como substituição e adição.






























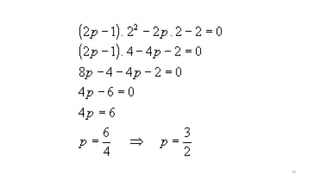




























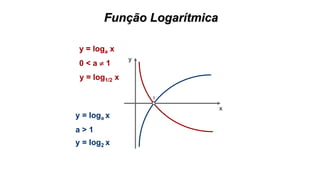
![INEQUAÇÕES DE 1º GRAU
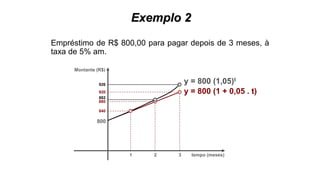
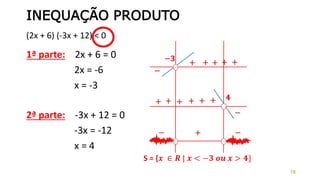
Resolva a inequação 2x + 8 > 0
2x + 8 > 0
2x > - 8
X >
x
+
-
S = ] – 4 , + [
X > - 4
- 4
S = { x lR / x > - 4 }
- 8
2
+
(Reta cresc.)](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-63-320.jpg)
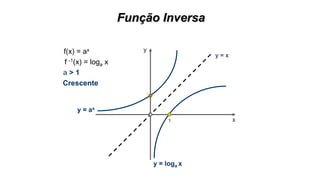
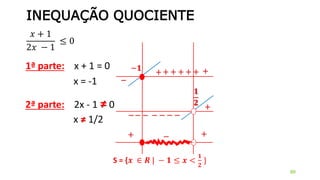
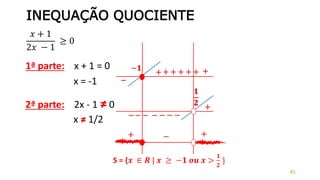
![INEQUAÇÕES DE 2º GRAU
Resolver a inequação X2 + 5x + 6 < 0
Concavidade para cima
x2 + 5x + 6 = 0
= 1
X = - 5 1
2
X’ = - 3 e x” = - 2 x- 3 - 2
+ +
-
S = {x lR / -3 < x < - 2}
S = ] –3, – 2 [](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-64-320.jpg)
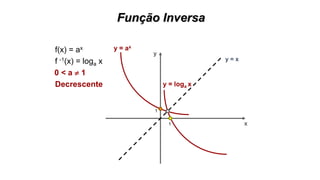
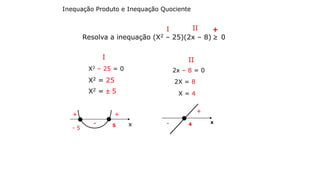
![SISTEMAS DE INEQUAÇÕES
Resolva o sistema
X2 – 36 > 0
X – 3 < 0
Conc. P/ cima
Reta crescente
X2 – 36 = 0
X2 = 36
X = 6
x-6 6
+ +
-
X – 3 < 0
X < 3
x3
+
-
I
- 6 6
II
3
I II
- 6
S = { x lR / x < - 6 }
S = ] - , - 6 [](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-65-320.jpg)
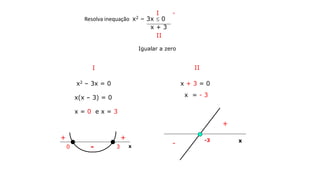
![Estudo do sinal
I
II
I . II
-5 4 5
-5 4 5
+ +
+ +
- -
- -
- -+ +
S = { x lR / - 5 x 4 ou x 5}
S = [– 5, 4] [5, + [](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-67-320.jpg)
![Estudo do sinal
I
II
I : II
-3 0 3
-3 0 3
++ - +
- + + +
- + - +
S = { x lR / x < - 3 ou 0 x 3 }
S = ] – , - 3[ [0, 3 ]](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-69-320.jpg)
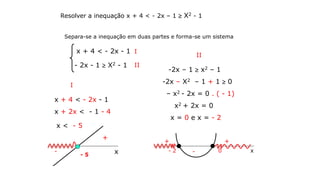
![Fazendo a interseção
I
II
I II
-5
-2 0
- 5
S = { x lR / x < - 5 }
S = ] – , - 5[](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-71-320.jpg)


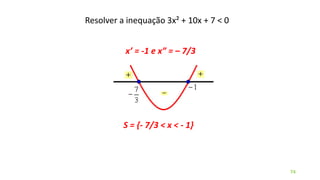
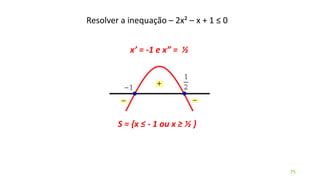





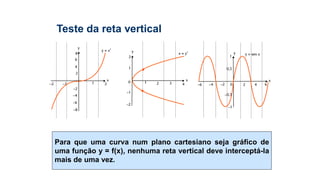
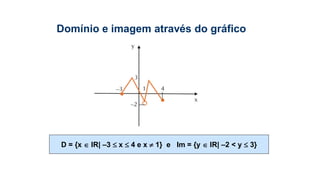
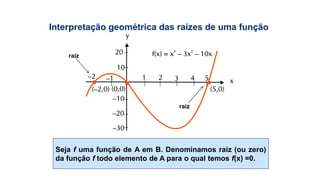

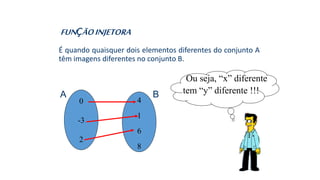
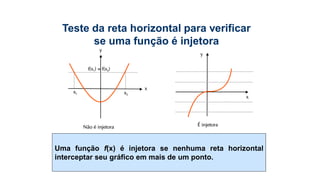
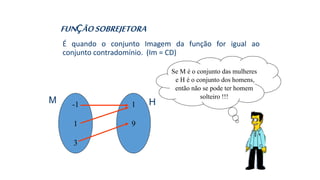
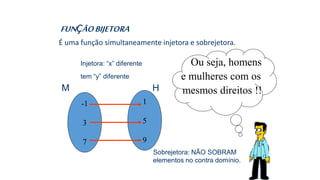
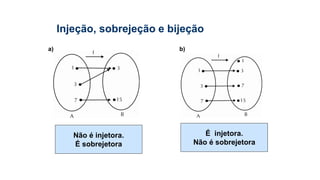
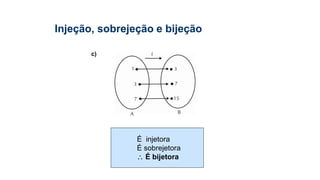
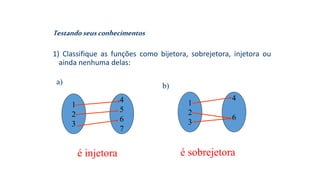
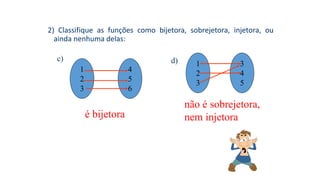
![3) Dada a função sobrejetora f : [2; 8] B, tal que f(x) = x² – 8x +7,
observe atentamente seu gráfico e determine seu domínio e imagem.
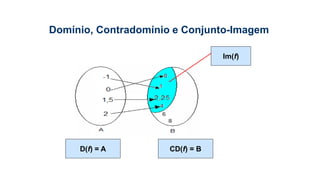
D(f) = [2;8]
Im(f) = [-9;7]
y
x
7
-5
2 4
7 8
-9](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-102-320.jpg)
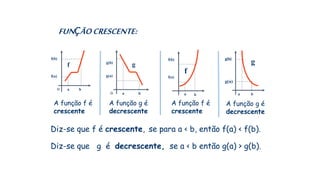
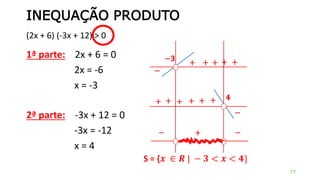
![6) A partir da análise do gráfico, determine os intervalos
onde a função é:
y
x-2 0 2 4 6
a) Decrescente: ]0, 4[
b) Crescente: ]-∞ ; 0[ e ]4 ; +∞[](https://image.slidesharecdn.com/cfsd2016-matematica-2v1-160126024506/85/CfSd-2016-matematica-2-v1-104-320.jpg)