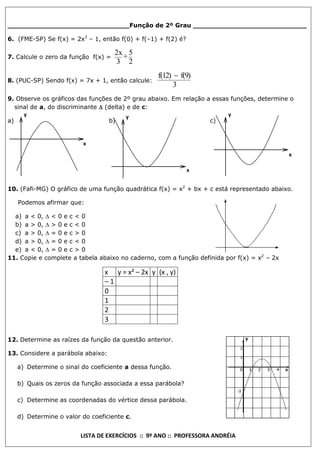
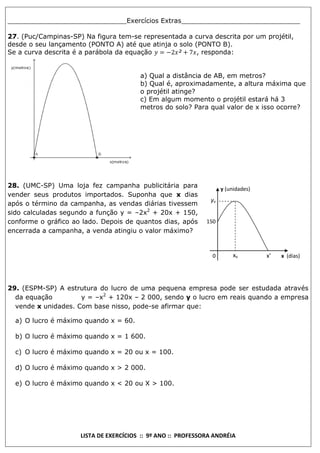
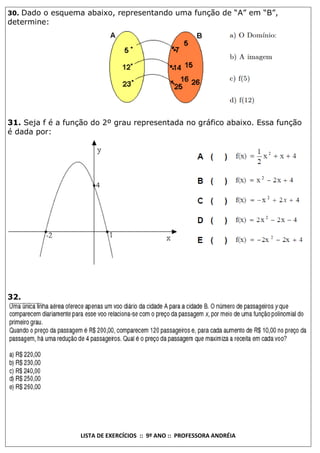
Este documento é uma lista de exercícios de matemática para o 9o ano preparada pela professora Andréia. Contém 32 exercícios sobre funções do 1o e 2o grau, probabilidade e situações-problema envolvendo funções. Os exercícios abordam conceitos como zeros de funções, vértice de parábolas, probabilidade e princípio da contagem.

1. LISTA DE EXERCÍCIOS DE MATEMÁTICA
PROFESSORA ANDRÉIA
Conteúdo da P2: Função do 1º grau e do 2º grau, Probabilidade e Situações Problemas de funções.
_____________________________Função de 1º Grau ___________________________
1. Observe o quadro abaixo e responda:
Número de
Refrigerantes
1
2
3
4
5
Preço a pagar
R$ 2,50
R$ 5,00
R$ 7,50
R$ 10,00
R$ 12,50
a) Qual o preço a ser pago por 3 refrigerantes? _____________
b) Quantos refrigerantes podem ser comprados com R$
17,50?
___________________________________________________
c) O preço a pagar está em função do número de refrigerantes
comprados?_________________________________________
d) Qual a lei de formação que determina o preço y a pagar numa
compra de x refrigerantes? _______________________
2. Observe, abaixo, a máquina que transforma números:
a) Observe o que a máquina faz. Em seguida, complete a
tabela abaixo:
Entrada
Entrada: x – 2
–1
0
1
2
3
4
Saída: y
Multiplica por
b) Qual a fórmula ou lei da função que nos dá y em função de x?
2 e diminui 3 .
Saída
___________________________________________________
3. Um botânico mede o crescimento de uma planta numa determinada hora do dia.
Altura (cm)
0
1
2
3
Tempo (em dias)
0
5
10
15
Se, num determinado período, essa relação entre tempo e altura for mantida, pergunta-se:
a) Que fórmula relaciona a altura x em função do tempo y? ________________________
b) Que altura a planta terá no 30º dia? ________________________________________
4. Determine algebricamente o(s) zero(s) de cada uma das seguintes funções:
b) y  
a) f(x) = 2x – 3
2
x 1
3
5. Observe abaixo o gráfico de uma função f de IR em IR e responda:
As coordenadas do zero da função e a intersecção com o eixo y são
respectivamente:
a)
b)
c)
d)
e)
(0, 0) e
(– 2, 2)
(0, – 2)
(2, 0) e
(– 2, 0)
(– 2,0)
e (0, 0)
e (0, 2)
(0, 2)
e (0, 2)
LISTA DE EXERCÍCIOS :: 9º ANO :: PROFESSORA ANDRÉIA

2. _____________________________Função de 2º Grau ___________________________
6. (FME-SP) Se f(x) = 2x3 – 1, então f(0) + f(–1) + f(2) é?
7. Calcule o zero da função f(x) =
2x 5
+
3 2
8. (PUC-SP) Sendo f(x) = 7x + 1, então calcule:
f(12)  f(9)
3
9. Observe os gráficos das funções de 2º grau abaixo. Em relação a essas funções, determine o
sinal de a, do discriminante  (delta) e de c:
y
y
y
a)
b)
c)
x
x
x
10. (Fafi-MG) O gráfico de uma função quadrática f(x) = x2 + bx + c está representado abaixo.
Podemos afirmar que:
a) a < 0,  < 0 e c < 0
b) a > 0,  > 0 e c < 0
c) a > 0,  = 0 e c > 0
d) a > 0,  = 0 e c < 0
e) a < 0,  = 0 e c > 0
11. Copie e complete a tabela abaixo no caderno, com a função definida por f(x) = x2 – 2x
x y = x² – 2x y (x , y)
–1
0
1
2
3
12. Determine as raízes da função da questão anterior.
13. Considere a parábola abaixo:
a) Determine o sinal do coeficiente a dessa função.
b) Quais os zeros da função associada a essa parábola?
c) Determine as coordenadas do vértice dessa parábola.
d) Determine o valor do coeficiente c.
LISTA DE EXERCÍCIOS :: 9º ANO :: PROFESSORA ANDRÉIA

3. 14. Os zeros da função quadrática de R em R definida por y = x2 – 2x – 15 são:
15. Determine as coordenadas do vértice das funções dadas por:
a) y = x2 – 4x – 5
b) y = –x2 + 4x – 3
16. Dada a função y = x2 + 2x – 3,
determine:
17. Dada a função y = –x2 + 4x – 3,
determine:
a) os zeros dessa função;
a) os zeros dessa função;
b) o vértice;
b) o vértice;
c) o valor máximo ou mínimo
c) o valor máximo ou mínimo;
__________________Probabilidade e Princípio da contagem_____________________
18. Um fabricante de disquetes de computador não poderá vender um lote que contenha mais de
5% de disquetes defeituosos. Um inspetor do controle de qualidade tomou uma amostra de 50
disquetes desse lote, e detectou que 2 deles estavam defeituosos, assim a probabilidade de se
tirar um disquete defeituoso da amostra dos 50 corresponde a?
19. No lançamento de um dado, qual a probabilidade de se obter um número menor que 5?
20. Cinco bolas pretas são numeradas 1, 2, 3, 4, e 5 e outras sete bolas brancas são numeradas
1, 2, 3, 4, 5, 6 e 7 e todas colocadas em uma urna. Se uma bola é escolhida ao acaso a
probabilidade que o número seja 1 ou 2 é?
21. Qual a probabilidade de ocorrer no máximo uma cara em dois lançamentos de uma moeda?
22.Uma urna contém 100 bolinhas numeradas de 1 a 100. Uma bolinha é escolhida aleatoriamente
e é observado o seu número. Qual probabilidade de o número ser múltiplo de 5? E a probabilidade
dele não ser múltiplo de 5?
23. Numa sacola estão bolas numeradas de 1 a 10. A chance de uma pessoa tirar uma bola
numerada com um número par é?
24. Num acidente automobilístico, depois de ouvidas várias testemunhas, concluiu-se que o
motorista culpado pelo acidente dirigia o veículo cuja placa era constituída de três vogais distintas e
quatro algarismos diferentes. Nessas condições, o número de veículos suspeitos pelo acidente é?
25. Com os algarismos 1,2,3,4,5 e 6, quantos números pares de 3 algarismos distintos podemos
formar?
26. Para acessar a internet, Gilberto Dunas escolheu uma senha formada por seis letras diferentes,
todas presentes no seu nome. A senha começa por consoante e vai alternando consoante e vogal.
Com isso Gilberto pode montar sua senha de quantas maneiras diferentes?
LISTA DE EXERCÍCIOS :: 9º ANO :: PROFESSORA ANDRÉIA

4. _____________________________Exercícios Extras_____________________________
27. (Puc/Campinas-SP) Na figura tem-se representada a curva descrita por um projétil,
desde o seu lançamento (PONTO A) até que atinja o solo (PONTO B).
Se a curva descrita é a parábola da equação
, responda:
a) Qual a distância de AB, em metros?
b) Qual é, aproximadamente, a altura máxima que
o projétil atinge?
c) Em algum momento o projétil estará há 3
metros do solo? Para qual valor de x isso ocorre?
28. (UMC-SP) Uma loja fez campanha publicitária para
vender seus produtos importados. Suponha que x dias
após o término da campanha, as vendas diárias tivessem
sido calculadas segundo a função y = –2x2 + 20x + 150,
conforme o gráfico ao lado. Depois de quantos dias, após
encerrada a campanha, a venda atingiu o valor máximo?
y (unidades)
yv
150
0
xv
x'
x (dias)
29. (ESPM-SP) A estrutura do lucro de uma pequena empresa pode ser estudada através
da equação
y = –x2 + 120x – 2 000, sendo y o lucro em reais quando a empresa
vende x unidades. Com base nisso, pode-se afirmar que:
a) O lucro é máximo quando x = 60.
b) O lucro é máximo quando x = 1 600.
c) O lucro é máximo quando x = 20 ou x = 100.
d) O lucro é máximo quando x > 2 000.
e) O lucro é máximo quando x < 20 ou X > 100.
LISTA DE EXERCÍCIOS :: 9º ANO :: PROFESSORA ANDRÉIA

5. 30. Dado o esquema abaixo, representando uma função de “A” em “B”,
determine:
31. Seja f é a função do 2º grau representada no gráfico abaixo. Essa função
é dada por:
32.
LISTA DE EXERCÍCIOS :: 9º ANO :: PROFESSORA ANDRÉIA