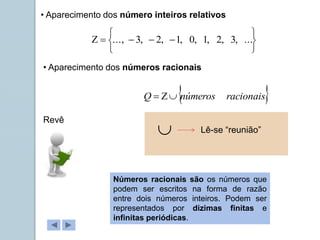
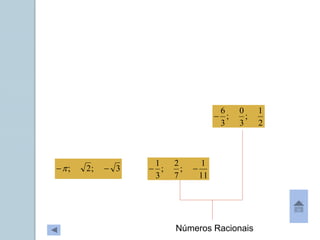
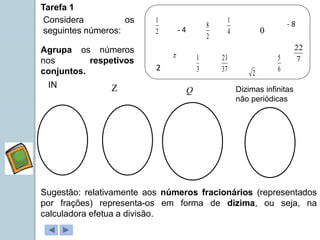
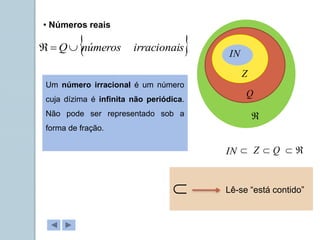
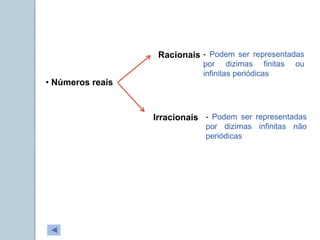
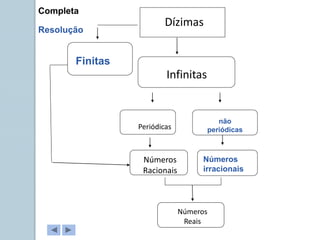
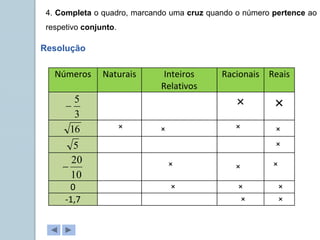
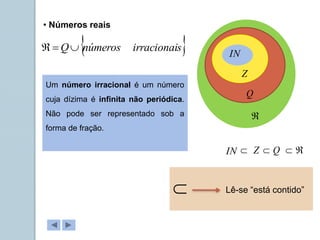
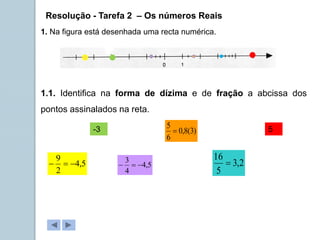
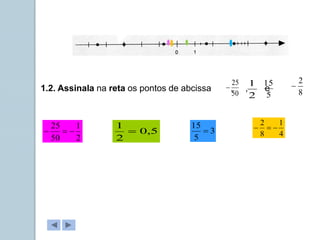
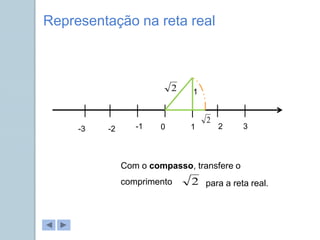
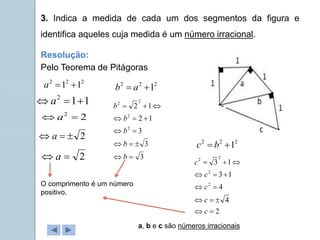
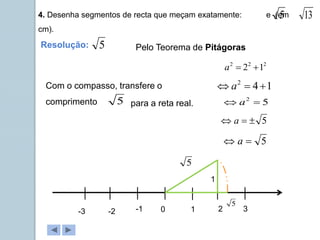
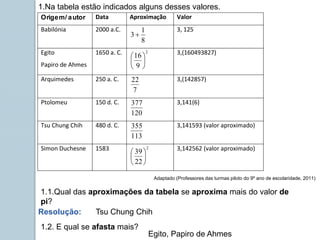
Este documento apresenta informações sobre números reais para o 9o ano. Apresenta a história dos números, desde os primeiros métodos de contagem até aos diferentes conjuntos numéricos como números naturais, inteiros, racionais e reais. Inclui também tarefas para classificar números nos respetivos conjuntos e exemplos de representação de números racionais e irracionais em forma de dizimas finitas e infinitas.

1. Números Reais
9.º Ano
Ano Letivo
2011/2012

2. Para saberes mais clica em
Para voltares atrás clica em
Para continuar clica em
Para confirmares a solução clica em
Instruções
Para reveres matérias clica em
Regressar à página
Para regressares ao início do capitulo –
Números Reais

3. 1- A História dos Números
3- Conjuntos Numéricos
2- Tarefa 1
4-Tarefa 2
5 -Tarefa 3
Números Reais – Parte 1
6 – Páginas da Internet que podes consultar

4. A história dos números
O número surgiu da necessidade que as pessoas tinham de
contar objetos e seres.

5. Nos primeiros tempos da humanidade, para
contar eram utilizados:
• os dedos,
• as pedras,
• os nós de uma corda,
• marcas num
osso/varas/paus/rochas...

6. • Mais tarde aparecem os símbolos
•Símbolos egípcios
• Aparecimento do número zero
• Ao longo dos séculos foram aparecendo novos
números
Começamos com os números naturais para contar objetos:
1, 2, 3, 4, …
IN={ 1, 2, 3, 4, …}
IN0={ 1, 2, 3, 4, …}

7. • Aparecimento dos número inteiros relativos










 ...
,
3
,
2
,
1
,
0
,
1
,
2
,
3
...,
• Aparecimento dos números racionais
 
racionais
números
Q 


Revê
Números racionais são os números que
podem ser escritos na forma de razão
entre dois números inteiros. Podem ser
representados por dizimas finitas e
infinitas periódicas.
 Lê-se “reunião”

8. Números Racionais
2
1
;
3
0
;
3
6

11
1
;
7
2
;
3
1


3
;
2
; 


9. 5
,
0
2
1

Dizima finita ou infinita de período zero.
...
3333333
,
0
3
1

Dizima infinita periódica de período três.
)
3
(
,
0
3
1

Ou seja,

2 ...
414213562
,
1
Dizima infinita não
periódica.
Uma dizima finita pode ser
considerada como infinita de
período zero.
O período de uma dizima
infinita periódica pode ser
formado por um ou mais
algarismos que se repetem.
...

10. Tarefa 1
Agrupa os números
nos respetivos
conjuntos.
Considera os
seguintes números:
IN  Q Dizimas infinitas
não periódicas
Sugestão: relativamente aos números fracionários (representados
por frações) representa-os em forma de dizima, ou seja, na
calculadora efetua a divisão.
2
1
3
1
4
1
6
5
2
- 4
2
- 8
2
8
37
21 7
22

0

11. 25
,
0
4
1

)
3
(
8
,
0
6
5

4
2
8

...
141592654
,
3


5
,
0
2
1

Dízima infinita não periódica
Dízima finita
Dízima finita
Dízima finita
Dízima infinita periódica

12. ...
414213562
,
1
2 
)
675
(
5
,
0
37
21

...
142857143
,
3
7
22

)
3
(
,
0
3
1
 Dízima infinita periódica
Dízima infinita periódica
Dízima infinita não periódica
Dízima infinita não periódica

13. Resolução - Tarefa 1
IN  Q
2
2
8
2
8
2
8
2
2
- 4
- 4
- 8
- 8
0
2
1
3
1
4
1
6
5
2
- 4
0
2
- 8
2
8
37
21 7
22

0
37
21
7
22
6
5
2
3
1

2
1
4
1
Dizimas infinitas
não periódicas
37
21

14. Dizimas
infinitas não
periódicas
Um número irracional é um número cuja dízima é
________________________.
Nota: os números do conjunto, designado por outros, representam
dizimas infinitas não periódicas. São considerados os números
___________________.
37
21
7
22
2

irracionais
infinita não periódica
Não pode ser representado sob a forma de fração.

15. • Números reais
 
s
irracionai
números
Q


IN  Z Q 
 
IN
Z
Q

Um número irracional é um número
cuja dízima é infinita não periódica.
Não pode ser representado sob a
forma de fração.
 Lê-se “está contido”

16. • Números reais
Irracionais
Racionais - Podem ser representadas
por dizimas finitas ou
infinitas periódicas
- Podem ser representadas
por dizimas infinitas não
periódicas

17. Tarefa 1+.
Agora continua a resolver a tarefa 1. Se tiver dúvidas consulte o
powerpoint.
Tarefa 1+ Resolução.
Para acederes à tarefa 1 clica em:
Para consultares a resolução da tarefa 1 clica em:

18. Tarefa 1 +
Usando a calculadora
2.1. Representa por uma dizima cada um dos números e
classifica-a.
a) b) c)
d) e) f)
5
7

8
1
9
17

11
57
13 64
,
0
4
,
1


Dízima finita
125
,
0

Dízima finita
)
8
(
,
1


Dízima infinita
periódica
Dízima infinita periódica
Dízima infinita
não periódica
Dízima finita
)
18
(
,
5
 ...
605551275
,
3
 8
,
0

Resolução

19. g)
h) i)
j)
l)
m)
n)
12
7
6
59
99
32
7
 110
312
7
13 2
3
Dízima infinita
periódica
Dízima infinita
periódica
Dízima infinita
periódica
Dízima infinita não
periódica
Dízima infinita
periódica
Dízima infinita não
periódica
Dízima infinita não
periódica
)
3
(
58
,
0
 )
3
(
8
,
9

)
32
(
,
0

...
645751311
,
2

 )
36
(
8
,
2

...
857142857
,
1

...
8660254038
,
0


20. 2.2. Relativamente às dízimas infinitas periódicas, indica o seu período.
c)
d)
9
17
 11
57
)
8
(
,
1


Período 8
Dízima infinita periódica
)
18
(
,
5

Dízima infinita
periódica Período 18
g)
i)
l)
12
7
6
59
99
32
110
312
Dízima infinita
periódica
Dízima infinita
periódica
Dízima infinita
periódica
Dízima infinita
periódica
)
3
(
58
,
0

)
3
(
8
,
9

)
32
(
,
0
 )
36
(
8
,
2

Período 3
h)
Período 3 Período 32
Período 36

21. 2.3. Dos números anteriores indica quais são racionais e irracionais.
a) b)
d) e) f)
5
7

8
1
9
17

11
57
13 64
,
0
4
,
1


Dízima finita
125
,
0

Dízima finita
)
8
(
,
1


Dízima infinita
periódica
Dízima infinita periódica
Dízima infinita
não periódica
Dízima finita
)
18
(
,
5
 ...
605551275
,
3
 8
,
0

Número Racional
Número Racional
Número Racional
Número Racional Número Irracional
Número Racional

22. g)
h) i)
j)
l)
m)
n)
12
7
6
59
99
32
7
 110
312
7
13 2
3
Dízima infinita
periódica
Dízima infinita
periódica
Dízima infinita
periódica
Dízima infinita não
periódica
Dízima infinita
periódica
Dízima infinita não
periódica
Dízima infinita não
periódica
)
3
(
58
,
0
 )
3
(
8
,
9

)
32
(
,
0

...
645751311
,
2

 )
36
(
8
,
2

...
857142857
,
1

...
8660254038
,
0

Número Racional
Número Racional Número Racional
Número Irracional
Número Racional
Número Irracional
Número Irracional

23. Dízimas
Infinitas
Periódicas
Números
Reais
Números
Racionais
Completa
Resolução
Finitas
não
periódicas
Números
irracionais

24. 4. Completa o quadro, marcando uma cruz quando o número pertence ao
respetivo conjunto.
Números Naturais Inteiros
Relativos
Racionais Reais
3
5
 × ×
16
5
10
20

0
-1,7
Resolução
× × ×
×
×
×
× × ×
× × ×
×

25. 5. Completa os espaços de modo a obter afirmações
verdadeiras, utilizando:
5.1. Os símbolos de (pertence) e (não pertence).
N
..........
3 ; N
.........
7
 ;
Q
..
..........
5
3
;


..........
7 ; 
 Z
.........
4 ; 
Q
..........
9
,
0 ;
Z
..........
5
,
1
 ; Z
.........
16 ; Q
........
7 ;

.........
0 ; 
.........
 ;

0
.........
4
0
.
 







 



Resolução

26. 5.2. os símbolos 
ou
Q
Z
N ,
,
.....
3
5
 ; .....
5 
 ; .....
9 
 ;
.....;
0003
,
0  ; .....
7
,
5 
 ; .....
9
,
1  .

ou
Q
Z
ou
N


ou
Q

ou
Q
ou
Z


27. 6. Escreva:
6.1. Três números naturais maiores que 15;
6.2. três números inteiros consecutivos não naturais;
6.3. três números reais negativos e não inteiros;
6.4. três números reais positivos não racionais.
Resolução
Por exemplo: 20, 30 e 40
Por exemplo:
Por exemplo:
Por exemplo:
-4, -3 e -2
, 30 e 40
20, 30

28. 7. Diga, justificando, se são verdadeiras ou falsas as
seguintes afirmações:
7.1. Todo o número real é racional.
7.2. Todo o número natural é inteiro.
7.3. Todo o número real é irracional.
Resolução
FALSO, Por exemplo pi é um número irracional logo real,
mas não é um número racional.
Verdadeiro.
Verdadeiro.
IN  Z
 
s
irracionai
números
Q



29. IN={ 1, 2, 3, 4, …}










 ...
,
3
,
2
,
1
,
0
,
1
,
2
,
3
...,
• Números inteiros relativos
 
racionais
números
Q 


• Números naturais
• Números racionais
Números racionais são os números que podem ser escritos na
forma de razão entre dois números inteiros. Podem ser
representados por dizimas finitas e infinitas periódicas.
Dizima finita
Dizima infinita periódica
Exemplos
5
,
0
2
1

...
3333
,
0
3
1

)
3
(
,
0
3
1

É o mesmo que
É uma dizima infinita
periódica de
período 3
Conjuntos Numéricos

30. • Números reais
 
s
irracionai
números
Q


IN  Z Q 
 
IN
Z
Q

Um número irracional é um número
cuja dízima é infinita não periódica.
Não pode ser representado sob a
forma de fração.
 Lê-se “está contido”

31. 
e
Q
Z,
 
,...
4
,
3
,
2
,
1


Z
dividem-se, ainda, em subconjuntos:
 
,...
4
,
3
,
2
,
1
,
0
0 

Z
 
1
,
2
,
3
,
4
..., 





Z
 
0
,
1
,
2
,
3
,
4
...,
0 





Z
 
positivos
racionais
números
Q 

 
negativos
não
racionais
números
Q 

0
 
negativos
racionais
números
Q 

 
positivos
não
racionais
números
Q 

0
 
positivos
não
reais
números


0
 
negativos
reais
números


 
negativos
não
reais
números


0
 
positivos
reais
números



32. Tarefa 2 – Os números Reais
1. Na figura está desenhada uma recta numérica.
1.1. Identifica na forma de dízima e de fracção a abcissa dos
pontos assinalados na recta.
1.2. Assinala na recta os pontos de abcissa , , e
50
25

2
1
5
15
8
2


33. Resolução - Tarefa 2 – Os números Reais
1. Na figura está desenhada uma recta numérica.
1.1. Identifica na forma de dízima e de fração a abcissa dos
pontos assinalados na reta.
5
,
4
2
9


 5
,
4
4
3



)
3
(
8
,
0
6
5

2
,
3
5
16

-3 5

34. 1.2. Assinala na reta os pontos de abcissa , , e
50
25

2
1
5
15
8
2

5
,
0
2
1
 3
5
15

2
1
50
25


 4
1
8
2




35. • A cada número real corresponde um ponto na reta e a cada
ponto da reta real corresponde um número real (a abcissa do
ponto).
Representação na reta real (exemplo)
1
1
?
Pelo Teorema de Pitágoras
2
2
2
1
1
? 

1
1
?2



2
? 


2
? 

2
?2


2. Represente na reta real o número irracional .2
O comprimento é um número
positivo.

36. 0 1 2 3
-1
-2
-3
1
2
2
Representação na reta real
Com o compasso, transfere o
comprimento 2 para a reta real.

37. 3. Indica a medida de cada um dos segmentos da figura e
identifica aqueles cuja medida é um número irracional.
Pelo Teorema de Pitágoras
2
2
2
1
1 

a
1
1
2


 a
2


 a
2

 a
2
2

 a
Resolução:
2
2
2
1

 a
b
3
3
3
1
2
1
2
2
2
2
2













b
b
b
b
b
2
2
2
1

 b
c
2
4
4
1
3
1
3
2
2
2
2













c
c
c
c
c
O comprimento é um número
positivo.
a, b e c são números irracionais

38. 4. Desenha segmentos de recta que meçam exatamente: e (em
cm).
5 13
Pelo Teorema de Pitágoras
2
2
2
1
2 

a
1
4
2


 a
5


 a
5

 a
5
2

 a
Resolução: 5
0 1 2 3
-1
-2
-3
1
5
5
Com o compasso, transfere o
comprimento 5 para a reta real.

39. 2
2
2
2
3 

a
4
9
2


 a
13


 a
13

 a
13
2

 a
Resolução:
0 1 2 3
-1
-2
-3
3
13
13
13
Pelo Teorema de Pitágoras
Com o compasso, transfere o
comprimento 13 para a reta real.

40. 3
4
4
,
1
5
8
2
)
6
(
,
1 

5. Coloca por ordem crescente
Resolução:
Primeiro separa os números positivos dos números negativos e
representa-os na forma de dízima.
•Números negativos: •Números positivos:
• Por ordem crescente:
....
4142
,
1
2 

 ...
6666
,
1
)
6
(
,
1 
40
,
1
4
,
1 


...
5874
,
1
4
3

6
,
1
5
8

)
6
(
,
1
5
8
4
4
,
1
2 3







41. 6. Indicar valores aproximados do número irracional .

...
141592
,
3

 Mas podemos escrever:
Enquadramento de  à unidade
Enquadramento de  à décima
Enquadramento de  à centésima
4
3 

2
,
3
1
,
3 
 
15
,
3
14
,
3 

Por defeito
Por defeito
Por defeito
Por excesso
Por excesso
Por excesso
Resolução:

42. 7. Completa com os símbolos >, < ou = de modo a obteres
afirmações verdadeiras.
7.1 -8 …….-9
7.2. -8 ….. 9
7.3. 7.4. 1,33……1,4
7.5. 9 …..-8
7.6
2
...
..........

2
...
.......... 

414213562
,
1
2
141592654
,
3



414213562
,
1
2
141592654
,
3






Resolução:
>
>
>
<
<
<

43. 8. Indica três números irracionais compreendidos entre 6 e 7.
Resolução:
6
36 
Escreve o número 6 e o número 7 em forma de raiz quadrada.
7
49 
Seja x um número real tal que: 7
6 
 x
49
36 
 x
Entre dois números reais, por
mais próximos que estejam,
existem infinitos números
racionais e irracionais.
Três números irracionais
podem ser, por exemplo:
38
37 45

44. Por volta do ano 4.000 a.C., algumas comunidades primitivas
aprenderam a usar ferramentas e armas de bronze.
As aldeias situadas nas margens dos rios transformaram-se em
cidades.
Surgiram novas actividades, devido ao desenvolvimento do
comércio.

45. Com isso algumas pessoas puderam dedicar-se a
outras actividades, tornando-se artesãos, comerciantes,
sacerdotes, administradores...
Os agricultores passaram a produzir alimentos em
quantidades superiores às suas necessidades.
Com as trocas comerciais surge o número zero e os
números negativos.

46. Como conseguiam efetuar cálculos rápidos e precisos com
pedras, nós ou riscos num osso?
Foi por necessidade imediata que estudiosos do Antigo Egipto
passaram a representar a quantidade de objetos de uma colecção
através de desenhos – os símbolos.
A criação dos símbolos foi um passo muito importante para o
desenvolvimento da Matemática.
Na Pré-História, o homem juntava 3 bastões com 5 bastões para
obter 8 bastões.
Hoje sabemos representar esta operação por meio de
símbolos.
3 + 5 = 8

47. 1 10 100 1.000 10.000 100.000 1.000.000
O sistema de numeração egípcio baseava-se em sete números-
chave:
Os egípcios usavam símbolos para representar esses números.
Um traço vertical representava 1 unidade:
Um osso de calcanhar invertido representava o número 10:
Um laço valia 100 unidades:

48. Uma flor de lótus valia 1.000:
Um dedo dobrado valia 10.000:
Com um girino os egípcios representavam 100.000 unidades:
Uma figura ajoelhada, talvez representando um deus, valia 1.000.000:

49. Todos os outros números eram escritos combinando os números-
chave.
Ao escrever os números, os egípcios não se preocupavam com a
ordem dos símbolos.

50. A necessidade de criação de números irracionais surgiu no tempo de
Pitágoras.
Os pitagóricos descobriram que existia um segmento de reta e que não
existia nenhum número que representasse o seu comprimento.
O segmento de reta era a diagonal de um quadrado de lado unitário.
Como eles só conheciam os números inteiros e os números
fraccionários, não conseguiam representar com estes números o
comprimento da referida diagonal.

51. Os incomensuráveis ou irracionais
As grandezas geométricas que não correspondiam a qualquer
número conhecido no tempo dos Gregos foram chamadas
incomensuráveis. Uma das mais célebres é a diagonal do
quadrado de lado 1, que hoje representamos por... (raiz
quadrada de 2).
Existem várias maneiras de demonstrar a impossibilidade de
exprimir essa medida usando um número inteiro ou fraccionário.
A mais simples de todas baseia-se no teorema de Pitágoras.

52. Um outro comprimento de representação geométrica simples e ao
qual não corresponde nenhum número da matemática grega é
o perímetro da circunferência (com diâmetro igual a 1 ou a outro
valor inteiro).
O valor desse perímetro é actualmente representado por pi.
Estas duas medidas, a da diagonal do quadrado de lado 1 e a do
perímetro da circunferência de diâmetro 1 têm valores
irracionais.
A definição rigorosa de número irracional foi dada só no
século XIX.

53. O número pi é um número irracional e representa a razão entre o
perímetro e o diâmetro de qualquer círculo. Em seguida dá-se um valor
aproximado de
Com as primeiras 50 casas decimais.

3751
69399
41971
50288
83279
26433
23846
89793
26535
14159
,
3


Tarefa 3
O número é um número com história. Utiliza-se, por exemplo,
quando se quer determinar a área ou o perímetro de um círculo. Ao
longo dos tempos foram utilizadas diferentes aproximações para o
valor de .



54. 1.Na tabela estão indicados alguns desses valores.
1.1.Qual das aproximações da tabela se aproxima mais do valor de
pi?
Origem/ autor Data Aproximação Valor
Babilónia 2000 a.C.
8
1
3 
3, 125
Egito
Papiro de Ahmes
1650 a. C. 2
9
16






3,(160493827)
Arquimedes 250 a. C.
7
22 3,(142857)
Ptolomeu 150 d. C.
120
377 3,141(6)
Tsu Chung Chih 480 d. C.
113
355 3,141593 (valor aproximado)
Simon Duchesne 1583 2
22
39






3,142562 (valor aproximado)
1.2. E qual se afasta mais?
Resolução:
Adaptado (Professores das turmas piloto do 9º ano de escolaridade, 2011)
Tsu Chung Chih
Egito, Papiro de Ahmes

55. 2. A avó da Joana vai colocar renda em volta da sua toalha redonda.
A toalha tem um metro de diâmetro. A Joana para saber qual o
comprimento de renda que a avó precisa de comprar, calculou o
perímetro da toalha. Verifica que a Joana obteve para o comprimento
da renda . Quantos metros deve a Joana comprar?
Resolução:
A Joana calculou o perímetro do círculo utilizando a seguinte fórmula:


 D
Pcírculo
Então

 

1
toalha
P
é o valor exacto da medida da renda a comprar.


No entanto, nestes problemas de ordem prática, não se usam os valores
exatos dos números irracionais, mas valores aproximados.

56. O que significa então metros de renda?

A Joana pega na calculadora e obtém:
141593
,
3

 valor aproximado a 6 casas decimais (10-6).
Porém, para comprar a renda não são necessárias tantas casas
decimais!
Vamos ajudar a Joana!!!

57. •Podemos pensar em duas casas decimais. É fácil verificar que
está entre 3,14 e 3,15, ou seja
15
,
3
14
,
3 
  , enquadramento de , às centésimas.
Repara que
• 3,14 m de renda não chega;
• 3,15 m de renda é um pouco mais, mas já chega.
Nota:
•3,14m=314cm
•3,15m=315cm

58. Podemos pensar noutros enquadramentos.
No nosso caso não interessa pois o “metro”da loja está graduado em
cm.
O valor que serve e o valor por excesso: 3,15 m.
Em cada situação é preciso ponderar qual é a aproximação mais
convenientes.

59. 3. Complete:
3.1.
3.1.1. utilizando uma casa decimal
3.1.2. utilizando duas casas decimais
3.1.3. utilizando três casas decimais
.......;
13
....... 

.......;
13
....... 

.
..........
13
..
.......... 

Resolução:
605551275
,
3
13 
6
,
3 7
,
3
60
,
3 61
,
3
605
,
3 606
,
3

60. 605551275
,
3
13 
3.2. Indique um valor aproximado de , por defeito, a menos
de 0,1.
13
3.3. Indique um valor aproximado de , por excesso, a menos de
0,01.
13
Resolução:
6
,
3
13  1 c.d.
61
,
3
13  2 c.d.