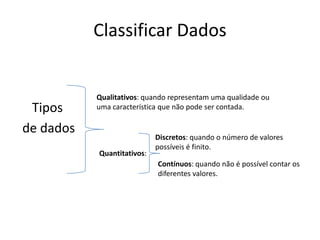
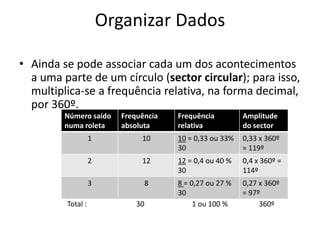
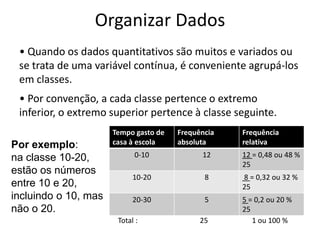
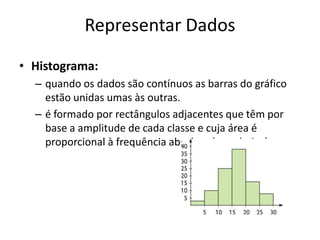
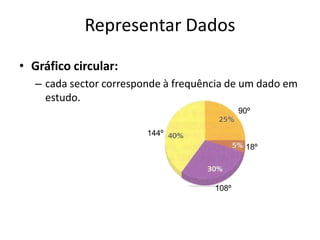
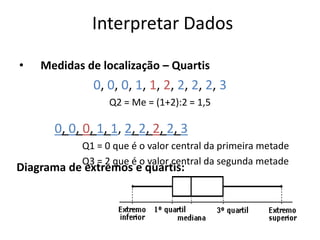
Este documento discute a organização e interpretação de dados estatísticos. Ele explica como classificar e organizar dados qualitativos e quantitativos em tabelas de frequência e como representar dados em gráficos de barras, histogramas e gráficos circulares. O documento também descreve medidas de localização como média, moda e mediana, e medidas de dispersão como amplitude e amplitude interquartis para interpretar conjuntos de dados.

1. Ano Letivo 2011/2012
Organização e
Tratamento de
Dados
Patrícia Almeida, 8º1

2. Classificar Dados
Qualitativos: quando representam uma qualidade ou
Tipos uma característica que não pode ser contada.
de dados
Discretos: quando o número de valores
possíveis é finito.
Quantitativos:
Contínuos: quando não é possível contar os
diferentes valores.

3. Organizar Dados
• Constrói-se uma tabela de frequências absolutas
(número de vezes que ocorre um determinado
acontecimento) e de frequências relativas
(quociente entre a frequência absoluta e o total de
elementos em estudo, que multiplicando por 100
nos dá a percentagem).saído Frequência
Número Frequência
numa roleta absoluta relativa
1 10 10 = 0,33 ou 33%
30
2 12 12 = 0,4 ou 40 %
30
3 8 8 = 0,27 ou 27 %
30
Total : 30 1 ou 100 %

4. Organizar Dados
• Ainda se pode associar cada um dos acontecimentos
a uma parte de um círculo (sector circular); para isso,
multiplica-se a frequência relativa, na forma decimal,
por 360º.
Número saído Frequência Frequência Amplitude
numa roleta absoluta relativa do sector
1 10 10 = 0,33 ou 33% 0,33 x 360º
30 = 119º
2 12 12 = 0,4 ou 40 % 0,4 x 360º =
30 114º
3 8 8 = 0,27 ou 27 % 0,27 x 360º
30 = 97º
Total : 30 1 ou 100 % 360º

5. Organizar Dados
• Quando os dados quantitativos são muitos e variados ou
se trata de uma variável contínua, é conveniente agrupá-los
em classes.
• Por convenção, a cada classe pertence o extremo
inferior, o extremo superior pertence à classe seguinte.
Tempo gasto de Frequência Frequência
Por exemplo: casa à escola absoluta relativa
na classe 10-20, 0-10 12 12 = 0,48 ou 48 %
25
estão os números
10-20 8 8 = 0,32 ou 32 %
entre 10 e 20, 25
incluindo o 10, mas 20-30 5 5 = 0,2 ou 20 %
não o 20. 25
Total : 25 1 ou 100 %

6. Percentagens
• Uma percentagem é uma razão de consequente 100.
Por exemplo: 12% significa 12 ou 0,12.
100
• Para criar uma percentagem, multiplica-se a razão por
100.
Por exemplo: Se numa turma com 25 alunos há 1
rapariga, a percentagem de raparigas é 4%, porque:
1 x 100 = 0,04 x 100 = 4.
25
• Para calcular uma percentagem, por exemplo 15% de
380, faz-se: 15 x 380 = 57.
100

7. Representar Dados
• Gráfico de barras:
– Deve ter um título e uma legenda em cada um dos
eixos;
– as barras têm a mesma largura, são separadas pelo
mesmo espaço e o seu comprimento é proporcional à
frequência que representam.

8. Representar Dados
• Histograma:
– quando os dados são contínuos as barras do gráfico
estão unidas umas às outras.
– é formado por rectângulos adjacentes que têm por
base a amplitude de cada classe e cuja área é
proporcional à frequência absoluta (ou relativa).

9. Representar Dados
• Gráfico circular:
– cada sector corresponde à frequência de um dado em
estudo.
90º
144º
18º
108º

10. Representar Dados
• Diagrama de caule-e-folhas:
– é um diagrama que utiliza uma parte do valor de cada
dado como caule e a outra como folha, para formar
grupos ou classes de dados.
O diagrama de caule-e-folhas também pode
ser usado para comparar duas distribuições.

11. Interpretar Dados
• Medidas de localização - Média
– Média (ou média aritmética) de um conjunto de
dados quantitativos é o valor que se obtém somando
todos os dados e dividindo o resultado obtido pelo
número de elementos desse conjunto.
– Só se pode determinar a média se os dados forem
numéricos.
Números de irmãos:
0, 1, 1, 3, 2, 2, 0, 2, 2, 0 Média
0+1+1+3+2+2+0+2+2+0 = 13 = 1,3
10 10

12. Interpretar Dados
• Medidas de localização - Média
– Para se determinar a média de um conjunto de dados
organizados numa tabela:
-Multiplica-se cada dado pela frequência absoluta
correspondente
-Adicionam-se esses produtos e divide-se a soma
pelo número total de dados.
– No caso dos dados estarem agrupados em classes,
procede-se do mesmo modo utilizando a marca da
classe como representante dos valores de classe.

13. Interpretar Dados
• Medidas de localização - Moda
– A Moda de um conjunto de dados é o valor ou
modalidade com maior frequência (ou que mais vezes
aparece). Indica o valor típico.
– Um conjunto de dados pode ter uma ou mais modas
ou não ter nenhuma.
– A moda tanto se pode determinar no caso dos dados
serem quantitativos, como qualitativos.
– No caso dos dados estarem agrupados em classes, a
classes que maior frequência chama-se classe modal.

14. Interpretar Dados
• Medidas de localização - Mediana
– A Mediana de um conjunto de dados numéricos é o
valor que ocupa a posição central; separa o conjunto
de dados em duas partes igualmente numerosas.
Representa-se abreviadamente por Med.
– A mediana, tal como a média, só se pode calcular
quando os dados são numéricos.
– Para determinar a mediana:
• Ordenam-se os dados e divide-se a amostra em
duas partes iguais.
• Se o número de dados é impar, a mediana é o valor
central
• Se o número de dados é par, a mediana é a média
aritmética dos dois valores centrais.

15. Interpretar Dados
• Medidas de localização - Mediana
– Com um número ímpar de dados
0, 0, 0, 1, 1, 2, 2, 2 ,2  O número 1 é a mediana da
amostra
– Com um número par de dados
0, 0, 0, 1, 1, 2, 2, 2 ,2 ,3  A mediana da amostra é a
média entre os dois valores centrais 1 e 2.
1 2
1,5
2

16. Interpretar Dados
• Medidas de localização - Quartis
– Os Quartis são os valores que separam um conjunto
de dados numéricos ordenados em quatro partes
igualmente numerosas, cada uma delas contendo
pelo menos 25% dos dados.
– Para determinar os quartis:
1. Ordenar os dados por ordem crescente
2. Determinar a mediana do conjunto de dados. Este
é o valor de Q2=Med.
3. Determinar a mediana dos valores que ficam à
esquerda de Q2. Este é o valor de Q1.
4. Determinar a mediana dos valores que ficam à
direita de Q2. Este é o valor de Q3.

17. Interpretar Dados
• Medidas de localização – Quartis
0, 0, 0, 1, 1, 2, 2, 2, 2, 3
Q2 = Me = (1+2):2 = 1,5
0, 0, 0, 1, 1, 2, 2, 2, 2, 3
Q1 = 0 que é o valor central da primeira metade
Q3 = 2 que é o valor central da segunda metade
Diagrama de extremos e quartis:

18. Interpretar Dados
• Medidas de Dispersão
– Amplitude é a diferença entre o valor máximo e o
valor mínimo da distribuição.
–Amplitude interquartis é a diferença entre o 3º e o 1º
quartis. Mede a dispersão dos dados em torno da
mediana.
–Um diagrama de extremos e quartis é uma forma
esquemática de representar os valores extremos
(máximo e mínimo) e os quartis de um conjunto de
dados. Permite visualizar rapidamente onde se
encontra a maior concentração de dados.