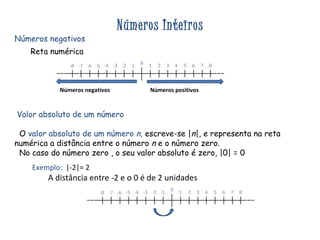
1) O documento discute conceitos básicos de números naturais, inteiros e racionais como múltiplos, divisores, primos, operações e representações decimais. 2) Inclui critérios de divisibilidade, máximo divisor comum, mínimo múltiplo comum e suas propriedades. 3) Aborda números negativos, valor absoluto, simetria e regras de adição, subtração, multiplicação e divisão de inteiros.

1. Números e Operações Ano Letivo 2011/2012 Jéssica Fernandes, 8º1

2. Números Naturais Múltiplos de um número é todo aquele que se obtêm multiplicando o número dado por um número inteiro qualquer. Exemplo : Múltiplos naturais de 2  M2 = {2,4,6,8,10,12...} 2x1= 2; 2x2= 4; 2x3= 6; ... Divisor de um número é um número natural que o divide num número inteiro de vezes . Exemplo: Divisores de 20  D20={1,2,4,5,10,20} 20=1x20 ; 20=2x10 ; 20=4x5

3. Números Naturais Critérios de divisibilidade por 2,3,4,5,9 e 10 Os critérios de divisibilidade permitem descobrir se um número é ou não divisível por um determinado número, sem efetuar o cálculo. Um número é divisível por 2 se for par. Um número é divisível por 3 se a soma dos algarismos que compõem o número for um múltiplo de 3. Um número é divisível por 5 se terminar em 0 ou 5. Um número é divisível por 10 se terminar em 0. Um número é divisível por 100 se terminar com dois 0. Exemplo: 126 é divisível por 2 pois trata-se de um nº par. 243 é divisível por 3 porque 2+4+3=9 (múltiplo de 3) 680 para além de ser divisível por 2 , é divisível por 5 e por 10, pois termina em 0 .

4. Números Naturais Número primo e número composto Um número inteiro maior que 1 é um número primo quando tem dois e só dois divisores: a unidade e o próprio número . Um número composto é um número que tem mais que dois divisores naturais distintos. Exemplos de alguns números primos  2,3,5,11,13,17,19,23...

5. Números Naturais Máximo divisor comum (m.d.c.) de dois números naturais é o maior dos divisores comuns a esses números. Mínimo múltiplo comum (m.m.c.) de dois números naturais é o menor dos múltiplos comuns a esses números. Exemplo: 63 = 9x7 27 = 9x3 = 3x3x7 = 3x3x3 m.d.c (27,63) = 3x3 = 9 m.m.c (27,63) = 3x3x3x7 = 189 3 3 3 7 63 27

6. Relação entre o m.d.c. e o m.m.c. de dois números O produto do máximo divisor comum e do mínimo múltiplo comum de dois números naturais é igual ao produto desses números. Exemplo : m.d.c. (27,63) = 9 m.m.c. (27,63) = 189 m.d.c.(27,63) x m.m.c.(27,63) = 9x189 = 1701 e 27x63 = 1701 Números Naturais

7. Números Inteiros Números negativos Reta numérica Valor absoluto de um número O valor absoluto de um número n, escreve-se | n |, e representa na reta numérica a distância entre o número n e o número zero. No caso do número zero , o seu valor absoluto é zero, |0| = 0 Exemplo: |-2|= 2 A distância entre -2 e o 0 é de 2 unidades Números negativos Números positivos

8. Números Inteiros Números simétricos Dois números simétricos não nulos são simétricos se e só se são diferentes e têm o mesmo valor absoluto. No caso do zero pode-se afirmar que simétrico do zero é zero. Exemplo: O simétrico de -3 é 3  -(-3) = 3 O simétrico de +4 é -4  -(+4) = -4 O simétrico de +2 é +2  -[-(+2)] = +2

9. Números inteiros Regras da adição de números inteiros A soma de dois números com sinais diferentes é um número cujo valor absoluto é a diferença dos valores absolutos das parcelas e cujo sinal é o da parcela com maior valor absoluto. A soma de dois números com o mesmo sinal é um número com esse sinal e cujo valor absoluto é a soma dos valores absolutos das parcelas. Exemplo: +4+(-3)= +1 +4 e -3 têm sinais diferentes: |+4| = 4 e |-3| = 3, logo |4-3| = 1 +4 > -3 fica o sinal da parcela +4 -10+(-5)= -15 -10 e -5 têm o mesmo sinal: |-10| = 10 e |-5| = 5, logo 10+5 = 15 mantens-se o sinal das parcelas, neste caso ‘-’ -5+(+5)= 0 A soma de dois números simétricos é zero

10. Número inteiros Subtração de números inteiros Subtrair dois números inteiros corresponde a adicionar ao aditivo o simétrico do subtrativo. Exemplo: 10 - (+3) = 10 + (-3) simétrico de +3 é -3. Multiplicação de números inteiros O produto de dois números de sinais contrários é um número negativo. O produto de dois números com o mesmo sinal é um número positivo. 1 é o elemento neutro da multiplicação. 0 é o elemento absorvente da multiplicação. Exemplo: -4 x (-2) = +8 +2 x (-1) = -2 +10 x (+1) = +10 +5 x (+2) = +10 -5 x (+10) = -50 -5 x 0 = 0 -5 - (-2) = -5 + (+2) Aditivo Subtrativo

11. Números inteiros Divisão de números inteiros A divisão é a operação inversa da multiplicação. Nem sempre o quociente de dois números inteiros é um número inteiro. A divisão de um número por zero não tem significado! Exemplo: -10 : (-2) = +5 +8 : (+4) = +2 -5 : (+2) = -2,5 +3 : 0 não tem significado

12. Números racionais Números racionais e dízimas Um número racional é um nº que pode ser escrito na forma de fração , com a e b números inteiros e b ≠ 0. A cada nº racional corresponde uma dízima finita ou infinita periódica. A cada dízima finita ou infinita periódica corresponde um nº racional. As dízimas infinitas não periódicas são dízimas que não têm uma sequência de algarismos que se repita. (por exemplo, a dízima de π ) Exemplos dízimas: Transformar uma dízima finita ou infinita periódica numa fração irredutível

13. Números Racionais Operações com números racionais Adição algébrica Nota : Caso os números não tenham o mesmo denominador, têm de se encontrar frações equivalentes com o mesmo denominador para proceder à adição. Exemplos:

14. Multiplicação Números Racionais Exemplos:

15. Divisão Números Racionais Exemplos: