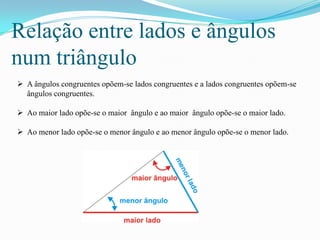
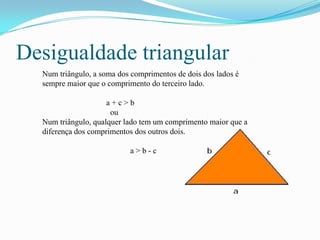
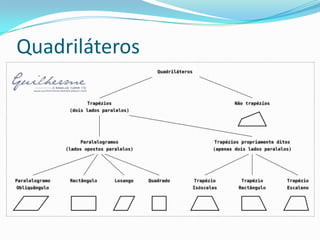
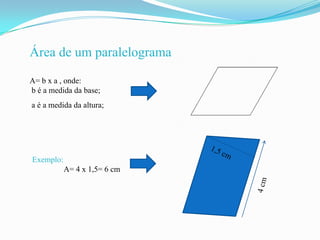
O documento apresenta os principais conceitos de geometria plana relacionados a ângulos, triângulos e polígonos. Inclui definições de ângulos opostos e paralelos, propriedades dos ângulos e lados de triângulos, critérios de congruência de triângulos, fórmulas para cálculo da soma dos ângulos internos e externos de polígonos e a fórmula para cálculo da área de um paralelogramo.

1. Ano Letivo 2011/2012
Inês Simões, 8º1

2. Ângulos verticalmente opostos
Dois ângulos dizem-se verticalmente opostos se têm o
vértice comum e os lados de cada um estão no
prolongamento dos lados do outro.
Dois ângulos verticalmente opostos são congruentes, ou
seja, têm a mesma amplitude.

3. Exemplo:
 Os ângulos AOB e COD são verticalmente opostos.
 Os ângulos DOB e COA são verticalmente opostos.
 AÔB = CÔD
 DÔB = CÔA

4. Ângulos de lados paralelos
 Dois ângulos de lados paralelos são geometricamente iguais, ou
suplementares.
 Vão ser geometricamente iguais se forem ambos agudos ou ambos obtusos.
 Vão ser suplementares se um for agudo e o outro obtuso.

5. Exemplo:
 Os ângulos BGE e DHG são ângulos de lados paralelos, logo, são
congruentes (BEG= DHG)
 O ângulo DHG e AGH são ângulos alternos internos, logo , são congruentes.

6. Ângulos num triângulo
 A soma das amplitudes dos ângulos internos de um
triângulo é 180º.
 A amplitude de um ângulo externo de um triângulo é
igual à soma das amplitudes dos ângulos internos não
adjacentes.
 A soma das amplitudes dos ângulos externos de um
triângulo é 360º.
60+60+60= 180º
(Ângulos internos)

7. Relação entre lados e ângulos
num triângulo
 A ângulos congruentes opõem-se lados congruentes e a lados congruentes opõem-se
ângulos congruentes.
 Ao maior lado opõe-se o maior ângulo e ao maior ângulo opõe-se o maior lado.
 Ao menor lado opõe-se o menor ângulo e ao menor ângulo opõe-se o menor lado.

8. Construção de um triângulo
Dois lados de um triângulo medem 2,5cm e 5,6 cm.
Qual é o comprimento do terceiro lado?
2,5 + 5,6 = 8,1
5,6 – 2,5 = 3,1
O terceiro lado pode ter qualquer comprimento desde que
seja maior que 3,1cm e menor que 8,1cm.

9. Desigualdade triangular
Num triângulo, a soma dos comprimentos de dois dos lados é
sempre maior que o comprimento do terceiro lado.
a+c>b
ou
Num triângulo, qualquer lado tem um comprimento maior que a
diferença dos comprimentos dos outros dois.
a>b-c

10. Critério de congruência de
triângulos
Critério LLL
Dois triângulos são congruentes se os seus lados tiverem o mesmos comprimento.

11. Critério LAL
Dois triângulos são congruentes se tiverem dois dos seus lados
e o ângulo por eles formado, respectivamente, conguentes.

12. Critério ALA
Dois triângulos são congruentes se dois dos seus ângulos tiverem a mesma
amplitude e o lado comum a eles tiver o mesmo comprimento.

13. ÂNGULOS EM POLÍGONOS
 A soma das amplitudes dos ângulos internos de um polígono com n lados é
dada pela fórmula (n-2) x 180º.
 A soma das amplitudes dos ângulos externos de qualquer polígono é 360º.
Soma das amplitudes dos ângulos Soma das amplitudes dos ângulos
internos: (4 – 2) x 180º= 360º internos: (5 – 2) x 180º= 540º

14. Quadriláteros

15. Área de um paralelograma
A= b x a , onde:
b é a medida da base;
a é a medida da altura;
Exemplo:
A= 4 x 1,5= 6 cm