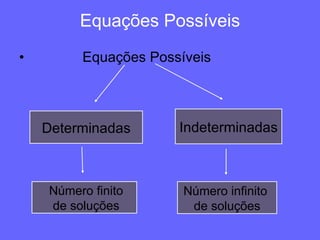
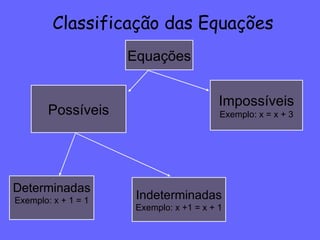
O documento classifica diferentes tipos de equações como possíveis/determinadas, possíveis/indeterminadas e impossíveis. Equações possíveis/determinadas têm um número finito de soluções. Equações possíveis/indeterminadas têm um número infinito de soluções. Equações impossíveis não têm solução.

1. 7.º ano 2008/9 Classificação das Equações

2. Equações Possíveis Determinar p de modo que a figura A seja um quadrado.

3. Equações Possíveis Os quadrados têm os lados geometricamente iguais. Se p + 2 = 8 a figura A é um quadrado. p + 2 = 8 p + 2 – 2 = 8 – 2 p = 6 A figura A é um quadrado se p = 6 A equação p + 2 = 8 é POSSÍVEL E DETERMINADA

4. Equações Possíveis Uma equação é POSSÍVEL E DETERMINADA se tem um número finito de soluções. Exemplo: p + 2 = 8 <=> p = 6

5. Equações Possíveis Determinar p de modo que a figura B seja um quadrado.

6. Equações Possíveis Se p + p = 2p a figura B é um quadrado. p + p = 2p p + p – 2p = 2p – 2p 0p = 0 -> Que significa???

7. Equações Possíveis 0p = 0 Se p = 1 -> 0 x 1 = 0 <=> 0 = 0 Verdade Se p = 2 -> 0 x 2 = 0 <=> 0 = 0 verdade … CONCLUSÃO: qualquer valor de p (positivo) é solução da equação p + p = 2p. Às equações que têm um número infinito de soluções classificam-se como POSSÍVEIS E INDETERMINADAS .

8. Equações Possíveis Equações Possíveis Determinadas Indeterminadas Número finito de soluções Número infinito de soluções

9. Equações Impossíveis A figura será um quadrado? A figura será um quadrado se: p = p + 1 p – p = p – p +1 0p = 1 -> Reparar que não existe nenhum número que multiplicado por zero seja igual a 1. A equação p = p + 1 não tem solução, é uma equação IMPOSSÍVEL .

10. Equações Impossíveis Uma equação é IMPOSSÍVEL quando não tem soluções. O conjunto – solução de uma equação impossível é o conjunto vazio e representa-se por { } ou Ø.

11. Classificação das Equações Equações Possíveis Impossíveis Exemplo: x = x + 3 Determinadas Exemplo: x + 1 = 1 Indeterminadas Exemplo: x +1 = x + 1