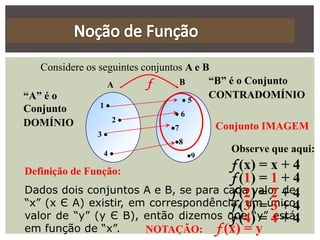
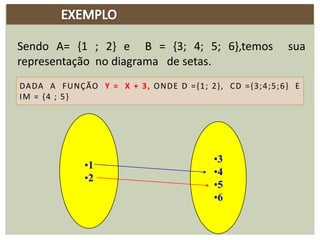
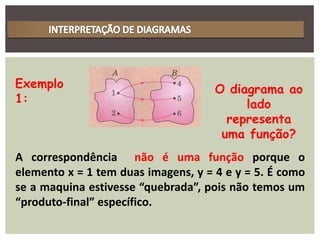
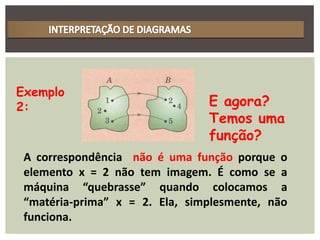
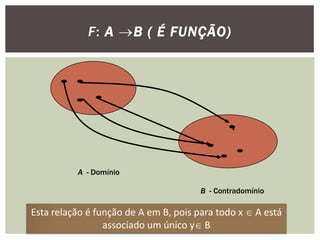
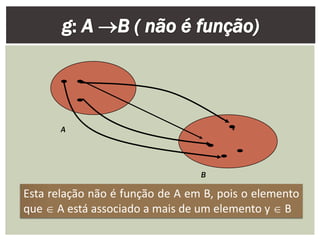
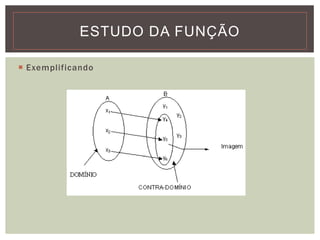
O documento discute funções, definindo-as como relações onde cada elemento de um conjunto domínio (A) é associado a exatamente um elemento de um conjunto imagem (B). Funções são importantes em diversas áreas como física, economia e biologia para explicar fenômenos nessas áreas. Exemplos de funções incluem tempo de viagem em função da distância, altura em função da idade e consumo de combustível em função da velocidade.

1. FUNÇÕES

2. As funções são importantes para explicar alguns fenómenos que acontecem na Física,
Economia, Biologia, Desporto, Medicina, Comércio, Tempo
 o tempo de viagem é função, entre outras coisas, da
distância percorrida.
 a altura de uma criança é função de sua idade;
 o consumo de combustível é função , entre outras
coisas , da velocidade.
 Perímetro de um triângulo é função da medida de
seus lados.

3. A FUNÇÃO
É COMO UMA MÁQUINA ONDE ENTRAM elementos
QUE SÃO TRANSFORMADOS E SAEM SUAS IMAGENS
Matematicamente...
y
Entra o “x”... ... E sai o “y”.

4. DEFINIÇÃO DE FUNÇÃO

5. Considere os seguintes conjuntos A e B
A f B “B” é o Conjunto
“A” é o 5
CONTRADOMÍNIO
Conjunto 1
6
DOMÍNIO 2
7 Conjunto IMAGEM
3
8
4 Observe que aqui:
9
Definição de Função:
f (x) = x + 4
f (1) = 1 + 4
Dados dois conjuntos A e B, se para cada valor + 4
f (2) = 2 de
“x” (x Є A) existir, em correspondência,(3) =único
f um 3 + 4
valor de “y” (y Є B), então dizemos que “y” 4 + 4
f (4) = está
em função de “x”. NOTAÇÃO: f (x) = y

6. Sendo A= {1 ; 2} e B = {3; 4; 5; 6},temos sua
representação no diagrama de setas.
DADA A F UNÇ ÃO Y = X + 3, ONDE D ={1; 2}, CD ={3;4 ;5;6} E
IM = {4 ; 5}
•3
•1
•4
•2
•5
•6

7. Exemplo O diagrama ao
1: lado
representa
uma função?
A correspondência não é uma função porque o
elemento x = 1 tem duas imagens, y = 4 e y = 5. É como
se a maquina estivesse “quebrada”, pois não temos um
“produto-final” específico.

8. Exemplo
2: E agora?
Temos uma
função?
A correspondência não é uma função porque o
elemento x = 2 não tem imagem. É como se a
máquina “quebrasse” quando colocamos a
“matéria-prima” x = 2. Ela, simplesmente, não
funciona.

9. F: A B ( É FUNÇÃO)
v
A - Domínio
B - Contradomínio
Esta relação é função de A em B, pois para todo x  A está
associado um único y B

10. A v
B
Esta relação não é função de A em B, pois o elemento
que  A está associado a mais de um elemento y  B

11. ESTUDO DA FUNÇÃO
 Exemplificando