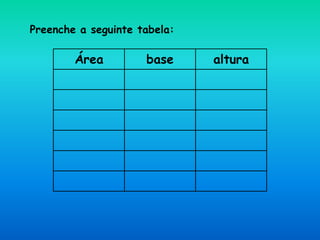
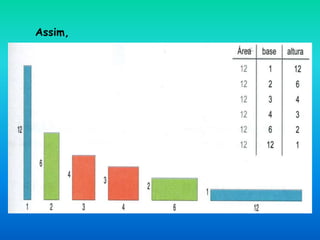
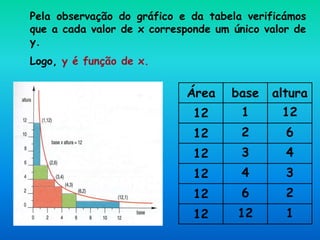
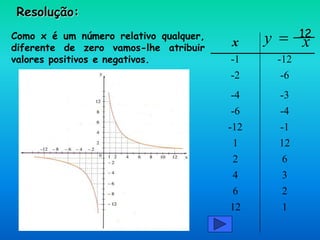
O documento descreve como construir retângulos de área constante usando 12 quadradinhos de 1 cm de lado. A relação entre a base e altura é de proporcionalidade inversa, onde o produto das duas dimensões é sempre igual a 12. Isso pode ser representado graficamente por uma hipérbole.

2. Com 12 quadradinhos iguais, com 1 cm de lado,
constrói vários retângulos, todos com a mesma
área.
Área do rectângulo = base x altura

3. Preenche a seguinte tabela:
Área base altura

4. Assim,

5. Que relação existe entre a
variação da base e da altura de
cada rectângulo?
Verifica-se que quando uma das dimensões
duplica, a outra reduz-se a metade; quando
uma triplica, a outra reduz-se à terça
parte,...
Ao aumento da base corresponde uma
diminuição da altura na mesma proporção
e vice-versa

6. O produto das duas dimensões é constante:
base x altura =12
Grandezas desta forma dizem-se inversamente
proporcionais.
Designando:
x medida da base e
y medida da altura
A relação x x y = 12 é uma proporcionalidade
inversa
12 é a constante de proporcionalidade

7. Uma Função é uma correspondência entre dois
conjuntos A e B, tal que a cada elemento de A
corresponde um e um só elemento de B

8. Pela observação do gráfico e da tabela verificámos
que a cada valor de x corresponde um único valor de
y.
Logo, y é função de x.
Área base altura
12 1 12
12 2 6
12 3 4
12 4 3
12 6 2
12 12 1

9. Podemos “arrumar” os rectângulos de área 12 e
dimensões inteiras num gráfico:
Verificamos que os
pontos estão sobre
uma curva a que se
chama hipérbole

10. Será que com as coordenadas de outros
pontos do gráfico é possivel descobrir mais
rectângulos de área 12?
Conhecendo a base, a altura é dada por:
x
y
12
=
=yx 12

11. Vejamos alguns exemplos:
base altura rectângulo coordenadas
x = 1,5 (1,5;8)
x = 2,5 (2,5;4,8)
x = 7,5 (7,5;1,6)
8
1,5
2,5
4,8
7,5
1,6
8
5,1
12
==y
8,4
5,2
12
==y
6,1
5,7
12
==y

12. Vamos “arrumar” estes novos rectângulos no
nosso gráfico:

13. Actividade:
Já representámos gráficamente
a função de proporcionalidade inversa
x
sabendo que x é um número positivo
(representa uma medida de comprimento).
xy
12
=
Representa gráficamente a função sabendo
que x é um número relativo qualquer diferente
de zero.

14. Resolução:
Como x é um número relativo qualquer,
diferente de zero vamos-lhe atribuir
valores positivos e negativos.
x
-1 -12
-2 -6
-4 -3
-6 -4
-12 -1
1 12
2 6
4 3
6 2
12 1
xy 12=

15. De um modo geral,
O gráfico de uma função
de proporcionalidade inversa
é sempre uma hipérbole.
Repara que a hipérbole
passa pelo ponto (1,k).
K é a constante de
proporcionalidade.
Numa função cujo domínio é
apenas o conjunto dos
números positivos ou apenas
o conjunto dos números
negativos, o gráfico é apenas
um ramo da hipérbole.

16. No gráfico de uma proporcionalidade inversa, o
produto das coordenadas de qualquer ponto é
sempre o mesmo – a constante de
proporcionalidade.
Uma função de proporcionalidade inversa pode
ser representada por uma expressão analítica, por
uma tabela ou por um gráfico.

17. De um modo geral,