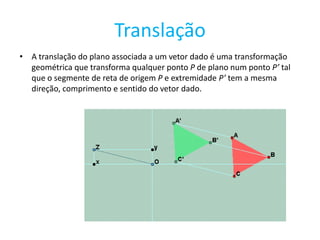
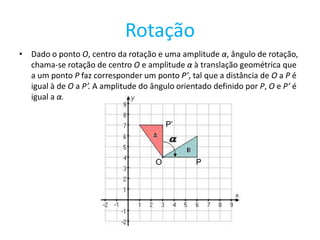
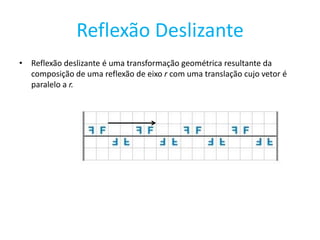
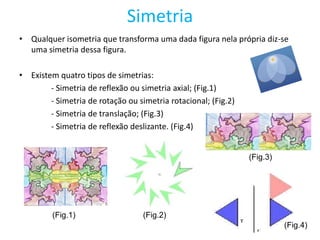
O documento descreve vários tipos de transformações geométricas e figuras planas. Resume as principais características de translação, reflexão, rotação e reflexão deslizante. Também define isometria, simetria, rosácea, friso e padrão, descrevendo os tipos de simetrias associadas a cada um.

1. BárbaraVeríssimo, 8º1

2. Translação
• A translação do plano associada a um vetor dado é uma transformação
geométrica que transforma qualquer ponto P de plano num ponto P’ tal
que o segmente de reta de origem P e extremidade P’ tem a mesma
direção, comprimento e sentido do vetor dado.

3. Reflexão
• Dada uma reta r (eixo de reflexão), dá-se o nome de reflexão do eixo r à
transformação geométrica que transforma os pontos de r em si próprios e
que, a cada ponto P não pertencentes a r, faz corresponder um ponto P’
tal que a distância de P a r é igual à distância de P’ a r e PP’ é
perpendicular a r.

4. Rotação
• Dado o ponto O, centro da rotação e uma amplitude α, ângulo de rotação,
chama-se rotação de centro O e amplitude α à translação geométrica que
a um ponto P faz corresponder um ponto P’, tal que a distância de O a P é
igual à de O a P’. A amplitude do ângulo orientado definido por P, O e P’ é
igual a α.
P’
O P

5. Reflexão Deslizante
• Reflexão deslizante é uma transformação geométrica resultante da
composição de uma reflexão de eixo r com uma translação cujo vetor é
paralelo a r.

6. Isometria
• Isometria é uma transformação geométrica que mantém a distância entre
pontos e preserva ângulos, isto é, a figura inicial e a transformada são
congruentes.

7. Simetria
• Qualquer isometria que transforma uma dada figura nela própria diz-se
uma simetria dessa figura.
• Existem quatro tipos de simetrias:
- Simetria de reflexão ou simetria axial; (Fig.1)
- Simetria de rotação ou simetria rotacional; (Fig.2)
- Simetria de translação; (Fig.3)
- Simetria de reflexão deslizante. (Fig.4)
(Fig.3)
(Fig.1) (Fig.2)
(Fig.4)

8. Rosácea
• Rosácea é uma figura plana cujo conjunto de simetrias possui as
seguintes características:
- O conjunto das suas simetrias é finito.
- Existe sempre um ponto do plano que é fixo para o conjunto das
simetrias da figura.
- As rosáceas têm sempre simetrias de rotação, podendo também ter
simetrias de reflexão.
- O centro das simetrias de rotação é sempre o mesmo, a amplitude
é um divisor de 360⁰C

9. Friso
• Friso é uma figura plana cujo conjunto de simetrias possui as seguintes
características
- O conjunto das suas simetrias é infinito;
- Em qualquer friso existe sempre uma infinidade de simetrias de
translação;
- Para além das simetrias de translação podem existir outras
simetrias;
- Existe sempre uma reta do plano que é fixa para todas as simetrias
do plano.

10. Padrão
• Padrão é uma figura plana cujo conjunto de simetrias possui as seguintes
caracteristicas:
- O conjunto das suas simetrias é infinito;
- Em qualquer padrão existe sempre uma infinidade de simetrias de
translação em mais do que uma direção;
- Para além das simetrias de translação podem existir outros tipos de
simetrias;
- Num padrão não há nenhum ponto nem nenhuma reta que sejam
fixos por todas as suas simetrias.