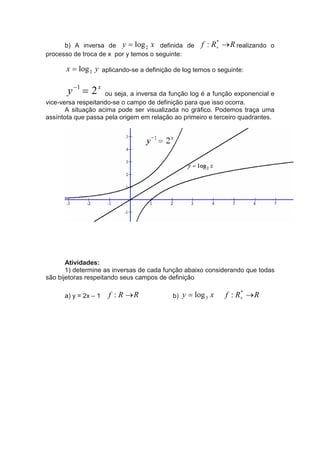
O documento apresenta uma introdução ao estudo de funções matemáticas. Aborda conceitos como domínio, imagem e contradomínio de funções, representações gráficas e algébricas de funções, funções exponenciais e logarítmicas, funções compostas e inversas. O texto destaca a importância histórica de matemáticos como Euler e Leibniz no desenvolvimento da teoria de funções.

1. AS FUNÇÕES
PROFESSORA: MARLEIDE COAN CARDOSO
Apostila 3

2. INTRODUÇÃO AO ESTUDO DAS FUNÇÕES
Para iniciar nossos estudos vamos responder algumas questões relacionadas
ao estudo das funções.
O que é uma função?
Quais as características que identificam uma função?
Quais as aplicações das funções?
Quais os matemáticos contribuíram com o estudo das funções?
Vamos iniciar nossos estudos a partir da observação e análise de alguns
gráficos encontrados em nosso contexto.

4. Escolha dois gráficos anteriores e identifique quando possível:
a) As grandezas variáveis envolvidas.
b) A grandeza dependente e a independente
c) O valor mínimo e o valor máximo
d) Os gráficos representam funções? Justifique sua resposta.
e) Identifique o domínio e a imagem de cada caso que representa função.

5. Vamos falar um pouco das funções e suas representações
Uma função pode ser representada em diferentes sistemas de representação, tais como:
Gráficos
Tabelas
Tempo ( min) Volume(em L)
5 300
10 200
20 100
35 0
Língua natural:
Em um reservatório havia 50 litros de água quando foi aberta uma torneira que despeja
dentro desse tanque mais 20 litros de água por minuto. A quantidade de água no tanque
é dada em função do número x de minutos em que a torneira fica aberta. Determine a lei
que representa a quantidade de água no reservatório em função do número de minutos
que a torneira fica ligada.
Representação algébrica
f(x) = 50 + 20x
No entanto nem sempre é possível representar uma mesma função em todos os
sistemas de representação.

6. As funções podem representar modelos ou padrões
(Prova Brasil 2007) As figuras mostradas abaixo estão organizadas dentro de um padrão
que se repete.
Mantendo-se essa disposição, a expressão algébrica que representa o número de pontos
da figura de ordem n (n=1,2,3,...)
Outro exemplo:
Se um tijolo de 8 furos para construção custa R$ 0,60, represente algebricamente e
graficamente o valor gasto para qualquer número de tijolos.
No entanto nem sempre é possível representar uma mesma função em todos os
sistemas de representação. Mas é importante discutir em sala de aula as possibilidades
que se dispõe para explicar um mesmo objeto matemático.
O estudo das funções constitui-se em uma das mais importantes ferramentas
matemáticas.
Hoje as funções apresentam aplicações na medicina, na geografia, na economia,
na química, botânica, zoologia, na engenharia e de um modo geral é utilizada para
compreender os fenômenos físicos, biológicos e sociais.
Entre os matemáticos que contribuíram significativamente com o estudo das
funções destaca-se Leonhard Euler.

7. De acordo com Boyer (1996), de 1727 a 1783, Euler
escreveu sobre matemática pura e aplicada,
praticamente na notação que utilizamos hoje, pois,
nenhum matemático foi tão responsável pela forma da
matemática de nível universitário quanto ele,
considerado o elaborador de notações mais bem
sucedido de todos os tempos.
Mas talvez a notação mais importante de todas seja a notação para a função
de Finalizando, nossas notações atuais são fundamentadas, principalmente, em Euler.
Outro matemático que apresentou SUS contribuições no estudo das funções foi
Gottfried Wilhelm von Leibniz
Leibniz não tinha só uma notável habilidade para
construir notações, mas também criou os termos
abscissa, ordenada, coordenada, eixo de coordenadas e
função.
A palavra função foi introduzida por Leibniz em 1673, para designar qualquer
das variáveis geométricas associadas com uma dada curva, aos poucos passou a
significar a dependência de uma variável em termos de outra ou outras variáveis.
Na atualidade função é definida como:
Uma função f é uma correspondência que atribui segundo uma lei qualquer, um
valor y a cada valor x da variável independentemente.
Escreve-se:
f :A→B ou A f B
→
→
Assim uma função f: A→B conta de 3 partes.
1) Um conjunto A chama – se domínio (onde a função está definida).
2) Um conjunto B chama –se contradomínio da função (onde f toma os valores)
3) Uma regra que permite associar cada elemento de x ∈ A a um único elemento f( x )
∈ B.
O conjunto A é o domínio de f e o conjunto B é o contradomínio de f. A natureza da
regra que ensina como obter o valor de f( x) ∈B quando é dado x ∈ A é inteiramente
arbitrária sendo sujeito a apenas duas condições:
1) Não deve haver exceções a fim de que f tenha o conjunto A como domínio, a
regra deve fornecer f(x) para todo x ∈ A.
2) Não deve haver ambiguidades, a cada x ∈ A, a regra deve fazer corresponder
um único f( x ) ∈ B.

8. Mas nem sempre uma relação entre duas grandezas representa uma função e
também o campo de definição de uma função pode ou não apresentar restrições em seu
domínio.
O estudo do domínio de uma função é um dos objetos matemáticos discutidos na
educação básica, vamos retomar o campo de definição de uma função em especial o seu
estudo do domínio.
DOMÍNIO, IMAGEM E CONTRADOMÍNIO
Dados dois conjuntos não vazios A e B, e uma lei f que associa a cada elemento
x de A um único elemento y de B, teremos uma função f de A em B para o qual
empregamos a seguinte linguagem:
Domínio da função - D(f) = A .
Imagem da função – Im(f) , sendo que Im está contida em B.
Contradomínio da função – CD(f) =B
Ao conjunto dos elementos y de B, que são imagens dos elementos x de A, dá-se o
nome de conjunto imagem ou simplesmente imagem da função.
O desenvolvimento da capacidade da análise gráfica auxilia os processos
resolutivos de muitas situações problemas encontrados em nosso contexto.
Vamos analisar alguns gráficos e determinar o seu domínio e imagem quando
possível.
a)
b)
c) d)

9. e) f)
g) h)
O ESTUDO DO DOMÍNIO DE UMA FUNÇÃO
Mas o campo de definição de uma função, pode ser analisado apenas
algebricamente.
Quando o domínio de uma função não está explícito, devemos considerar para este
domínio todos os valores reais de x que tornam possíveis, em R as operações indicadas
na fórmula matemática que defina a função.
Ex.: Determine o domínio das funções abaixo:
x x
a) f(x) = b) g(x) = ( x − 1) c) f(x) =
x−5 ( x − 3)

10. 2 1 x
d) y = e) y = 3 5 x + 1 f) y = +
x −4
2
x x+2
g) f(x) = 5x – 3 h) g(x) = x2 - 3x + 1
Exemplos.:
1) Dados os conjuntos A = {-2,-1, 0,1,2} e B = {-1,0,1,2,3,4,5,6}, e a função de A
em B expressa pela equação y = - x + 1, determinar:
a) Domínio da função;
b) CD(f)
c) Imagem da função
d) Representação gráfica
2) Dado A = {-1,0,1,2,3}, e a função f: A em R, definida por f(x) = x2+2x,
determine:
a) Domínio da função;
b) CD(f)
c) Imagem da função
3) Dado A = {-2,-1,0,1,2}, e B = { -2,-1,0,1,2,3} e a função de A em B expressa
pela equação y = x + 1 determine:
a) Domínio da função;
b) CD(f)
c) Imagem da função
d) represente graficamente.

11. Vamos pensar na seguinte situação o perímetro do quadrado em função
do lado p = 4 l observando seu campo de definição.
Mas se desejamos escrever o perímetro em função do lado temos que
p
l=
4
Veja na tabela de valores como isso ocorre
l p=4l p l = p/4
1 4 4 1
2 8 8 2
3 12 12 3
4 16 16 4
Veja no Gráfico como isso ocorre:
Assim em algumas situações podemos realizar a inversão das
grandezas variáveis, esse processo é denominado de função inversa.

12. Uma função será inversa se ela for bijetora. Se f : A→B é considerada
bijetora então ela admite inversa f : B→A. Por exemplo, a função y = 3x - 5
x+5
possui inversa y = y −1 = , observe o diagrama desta situação
3
Neste caso pode-se estabelecer a seguinte diagramação:
Note que a função possui relação de A→B e de B→A, então podemos
dizer que ela é inversa.
Pode-se também observar que entre a função e sua inversa há uma
troca entre o domínio e a imagem das mesmas. Isto possibilita que
algebricamente a inversa seja determinada pela troca de x por y conforme
segue:
No caso anterior temos o seguinte:
y = 3x – 5 efetuando-se a troca de x por y temos:
x = 3y – 5 agora realizando o processo de isolar o y temos
x + 5 = 3y
3y = x + 5
x+5
y −1 = ou seja a função inversa de y = 3x – 5
3
Vejamos outros exemplos:

13. b) A inversa de y = log 2 x definida de f : R+ → R realizando o
*
processo de troca de x por y temos o seguinte:
x = log 2 y aplicando-se a definição de log temos o seguinte:
y −1 = 2 x ou seja, a inversa da função log é a função exponencial e
vice-versa respeitando-se o campo de definição para que isso ocorra.
A situação acima pode ser visualizada no gráfico. Podemos traça uma
assíntota que passa pela origem em relação ao primeiro e terceiro quadrantes.
Atividades:
1) determine as inversas de cada função abaixo considerando que todas
são bijetoras respeitando seus campos de definição
a) y = 2x – 1 f : R →R b) y = log 3 x f : R+ → R
*

14. FUNÇÃO COMPOSTA
Vamos analisar a seguinte situação problema:
Uma festa de aniversário geralmente são consumidos 10 salgadinhos por pessoa, cada
salgadinho custa R$ 0,32. Qual a representação algébrica do valor gasto na festa em
função do número de pessoas e do valor do salgadinho (considere y = nº de salgadinho,
p (nº de pessoas) e v (valor gasto) ou V(y(p)). De o domínio da composta.
Definição: Dados as funções f : A → B e g : B →C , denominamos a
função composta de g e f a função g o f : A → C que é definida por
g(f(x)) = f(g(x)) e x.
Veja a imagem:

15. Exemplos:
1) Dado a função f(x) = x² - 2x + 1 e g(x) = 2x + 1 determine:
a) f(g(x)) b) g(f(2)) c) f(f(19))
2) Se f e g são funções tal que f(x) = 3x – 1 e f(g(x)) = x determine g(x)
Atividades
1) Dado f(x) = 2x -3 e g(x) = x² - 1, obtenha:
a) f(g(2)) b) g(g(3)) c) f(f(x))
d) f(f(x)) = 3 e) f(g(x)) f) f(g(x))
Conforme destacado anteriormente vamos ressaltar neste estudo as principais
características de cada função.
Vamos iniciar nossos estudos pela função exponencial e logarítmica.
O que caracteriza uma função exponencial?
Qual a relação com a função logarítmica?
O que caracteriza cada uma das funções?

16. FUNÇÃO EXPONENCIAL
Os Babilônios, foram os primeiros a utilizar potências, quando calculavam juros
compostos, utilizavam uma expressão que corresponde hoje a função exponencial
M = P.(1 + i ) n , sendo M o montante, P o valor inicial i a taxa e n o período.
A função exponencial pode ser aplicada a resolução de outros problemas, como
prever crescimento populacional, analisar epidemias, prever produções em empresas,
determinar a idade dos fósseis, decomposição de sustâncias, árvore genealógica, etc.
A função f: R em R dada por f(x) = ax ( com a ≠ 1 e a > 0) é denominada função
exponencial de base “a” e definida para todo x real.
Ex.: Represente graficamente as funções abaixo e determine o domínio e a imagem e
verifique se as funções são crescentes ou decrescentes:
a) f(x) = 2x b) f(x) = (1/2)x
a >1 ( crescente) 0< a < 1 ( decrescente)
Característica da função exponencial no gráfico
Outros exemplos:
1) Dado as funções abaixo represente-as graficamente, verifique se são crescentes ou
decrescentes, determine o domínio e a imagem, o ponto onde f(x) corta o eixo y.
a) f(x) = 5x b) f(x) = (1/5)x
2) Represente no plano cartesiano as funções considerando que são definidas em R
determine a imagem.
x
3
a) f(x) = 2 x +1 b) g(x) =  
4

17. x
4
c) y =   d) g(x) = - 3 x
3
Conforme já estudamos o logaritmo pode ser representado como uma
equação exponencial, também a função logarítmica é a inversa da função
exponencial
FUNÇÃO LOGARITMICA
Definição:
Seja um número real a ∈ R tal que a > 0 e a ≠ 1 . Denomina-se função logarítmica a
função f: R+ → R, dada por:
*
f(x) = loga x
Ex.: Construa o gráfico das funções abaixo e determine o domínio e a imagem.
a) f(x) = log 3 x b) f(x) = log 1 x c) g(x) = log 3 ( x − 1)
3
Observando os gráficos construídos anteriormente identifique qual função é
crescente e qual função é decrescente. O que diferencia uma função da outra? O que se
pode concluir em relação ao crescimento das funções logarítmicas?
Características da função logarítmica
a>1 ( crescente) 0 < a <1 ( decrescente)

18. Outros exemplos:
1) Construa o gráfico das funções abaixo, determine o domínio e a imagem e verifique
se são crescentes ou decrescentes.
a) y = log 2 x b) y = ln x c) y = log 1 x
2
FUNÇÃO MODULAR
DEFINIÇÃO:
Denomina-se função modular a função f(x) = | x | de R em R, definida
por:
 x, se ≥ 0
f(x) = 
− x, se x< 0
Ex.: Se f: R em R é dada por f(x) = | -x + 5 |, calcule:
a) f(-1) b) f(1/2) c) f(-3)
CONSTRUÇÃO DE GRÁFICOS DA FUNÇÃO MODULAR
Ex.: Características da função modular
f(x) = | x2 –x –2| f(x) = | x – 2 | f(x) = | x | - 2

19. 1) construa o gráfico das funções modulares abaixo:
a) f(x) = | x – 2 | b) f(x) = |x -1 | - 2 c) f(x ) = | x +1 | + | x – 2|
d) f(x) = | x2 – 9| e) f(x) = | x | + | x – 1 | f ) f(x) = | x2 - 2 x – 8 |
2) Represente no mesmo gráfico as funções abaixo:
a) f(x) = | x | b) f(x) = | x | + 1 c) f(x) = | x | - 1

20. Seguindo nossos estudos sobre as funções elementares, vamos conhecer agora a
função do segundo grau, ou seja, as funções que caracterizam-se pela representação de
uma parábola.
FUNÇÃO POLINOMIAL DO 2º GRAU
Veja o problema a seguir:
Agora vamos aprofundar os estudos na função do segundo grau e seus
elementos

21. Outro problema
1) Um foguete carregando um satélite, depois de lançado, caiu, devido a um
pane do sistema. Ao estudar sua trajetória e as causas do acidente, a equipe
da base construiu o seguinte gráfico, que mostra a altura (y) alcançada pelo
foguete em função do tempo (t) decorrido após o lançamento.
Determine:
a)A altura máxima aproximada que o foguete atingiu;
b) O tempo que o foguete levou para atingir o ponto mais alto;
c) o tempo que o foguete levou para atingir a altura inicial;
d) a altura inicial;
1) A trajetória da bola , num chute a gol, descreve aproximadamente uma
parábola. Supondo que a sua altura h, em metros, t segundos após o chute,
dada por h = - t² + 6t, determine:
a) Em que instante a bola atinge a altura máxima?
b) Qual a altura máxima da bola?
c) Qual o intervalo crescente?
d) Qual o intervalo decrescente?
e) Em que instante a bola retorna ao solo?
f) Determine o valor de:
f(1)
f(3)
f(9)
DEFINIÇÃO:
Chama-se função polinomial do 2º grau ou função quadrática a função f: R em
R onde f(x) = ax2 + bx + c e os números a, b, c pertencem aos reais e a ≠ 0.
REPRESENTAÇÃO GRÁFICA DA FUNÇÃO POLINOMIAL DO 2º GRAU
Graficamente a função do 2º grau representa uma parábola.
Ex.: Construa o gráfico das funções abaixo:
a) f(x) = x2 – 2x - 3 b) f(x) = - x2 – 4x

22. ZEROS OU RAÍZES DE UMA FUNÇÃO POLINOMIAL DO SEGUNDO GRAU
Representam os valores que anulam a função. graficamente são os
pontos de intersecção da parábola com o eixo x (eixo das abscissas) . No
entanto, dentro do conjunto R existem funções do segundo grau que não
apresentam raízes reais. Quem determina a existência ou não de raízes reais é
o delta. Identifique as raízes das funções abaixo.
a) b)
c) d)
e)
f)

23. ESTUDO DO DELTA
O delta determina a existência ou não das raízes da função.
1º caso ∆ > 0 ( existem duas raízes reais e diferentes) ( intercepta o eixo
das abscissas em dois pontos
2º caso : ∆ < 0 (não existe raízes reais) não intercepta o eixo das abscissas
3º caso: ∆ = 0 ( uma raiz real ou zero duplo) tangencia o eixo das abscissas
Exemplos:
1) Determine as raízes reais (se existir) das funções abaixo e faça o esboço do
gráfico.
a) f(x) = x2 – x +4 b) f(x) = - x2 + 4x - 6
c) f(x) = x2 + 2x + 1 d) f(x) = x2 + 2x – 8
e)Determine m para que a função dada por f(x) = x 2 − 3x + m tenha duas raízes
reais.

24. CONCAVIDADE DA PARÁBOLA
Quem determina a concavidade da parábola é o “a” , assim :
a > 0 = concavidade para cima;
a < 0 = concavidade para baixo;
Exemplos:
Em cada caso determine a concavidade da parábola:
a) f(x) = x2 – x +2 b) f(x) = - x2 + 4x - 6
c) f(x) = -2 x2 + 2x + 1 d) f(x) = x2 + 2x – 8
FORMA FATORADA DA EQUAÇÃO DO 2º GRAU
ax 2 + bx + c = 0 ⇒ a ( x − x' ).( x − x" ) =0
Exemplos .: Escreva da forma fatorada as equações abaixo:

25. a) x 2 − x − 2 = 0 b) 2 x 2 − 5 x + 2 = 0 c) x 2 − 9 = 0
ESTUDO DO VÉRTICE
Observe o problema:
O lucro, em reais, de uma empresa na venda de determinado produto é dado pela função
2
L(x) = – 2x + 300x – 16, onde L(x) é o lucro e x representa a quantidade de produtos vendidos.
Determine o lucro máximo obtido pela empresa na venda desse produto
O vértice representa o ponto máximo quando ( a < 0) ou o ponto mínimo
( a > 0) de uma função do segundo grau. O vértice pode ser calculado com a
−b −∆
fórmula : V = , 
 2a 4a 
O yv é o ponto de referência para determinar a imagem.
.
Ex.: Encontre as coordenadas do vértice das funções abaixo:
a) f(x) = x2 + 2x +1 b) g(x) = - x2 + 4x –6 c) h(x) = x2 + 2x – 3
Atividades:
1)Determine o vértice das funções abaixo e o identifique como máximo ou
mínimo:
a) f(x) = x2 – 4 b) f(x) = - 3x2 – 5x c) f(x) = -x2

26. ESTUDO DO SINAL DA FUNÇÃO POLINOMIAL DO 2º GRAU
Estudar o sinal de uma função é determinar os valores de x para os
quais a função é positiva, negativa ou igual a zero.
Tudo o que está acima do eixo x é positiva e abaixo do eixo x é negativa.
Ex.: Faça o estudo do sinal das funções abaixo:
a) f(x) = x2 – 4 b) f(x) = - x2 – 5x c) g(x) = - x2 + 4x –
Exercício resolvido:
1) Observe o gráfico da função f(x) = x² -2x -3 ou pode ser representada na
forma fatorada f(x) = (x+1)(x-3) agora vamos observar seus pontos notáveis:
9
y f(x)=x^2-2x-3
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

27. a) A concavidade voltada para cima pois a = 1 ou seja a > 0;
b) as raízes: representam os pontos que passam pelo eixo x, no caso x’ = -
1 e x” = 3
c) O ponto de intersecção com o eixo das ordenadas corresponde ao valor
de c, ou seja no caso -3.
d) O domínio corresponde os valores que podem ser substituídos no x, no
caso é todos os reais, as parábolas em geral quando não representam
situações problemas são R, ou então quando determinamos a inversa
precisamos fazer a restrição no domínio.
e) Para determinar a imagem, deve-se levar em consideração o ponto mais
baixo uma vez que a concavidade é voltada para cima, então a imagem
é Im = { y ∈ R / y ≥ −4}
Considera-se que a referencia para o conjunto imagem corresponde ao
valor do vértice y, ou seja,
−∆
Im = { y ∈ R / y ≥ } se a > 0
4a
−∆
Im = { y ∈ R / y ≤ } se a < 0
4a
f) O ponto de vértice corresponde ao ponto mínimo ou ponto máximo
conforme o caso:
−b −∆
V =( , ) é o ponto máximo se a < o e mínimo se a > o.
2a 4a
No caso o vértice será V = (1,−4) como a = 1 , b= -2 e ∆ = 16 então
−b −2 − ∆ − 16
xv = = =1 e yv = = =−4
2a 2 4a 4

28. 2) Observe o gráfico e responda:
a) Qual o domínio e a imagem da função representada no gráfico?
3) O custo para produzir x unidades de certo produto é dado por
C (x) = 2x² - 100x + 5000, encontre:
a) O valor do custo mínimo
b) O valor de x para o qual o custo é mínimo.
4)Dado o gráfico abaixo responda as questões que se pede
10 y f(x)=x^2 -2x-3
9
8
7
6
5
4
3
2
1 x
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10
-1
-2
-3
-4
-5
-6
a) O domínio da função
b) O conjunto imagem
c) Intervalos crescentes e decrescentes.
d) As coordenadas do vértice
e) f(4) f(-2) f(1)

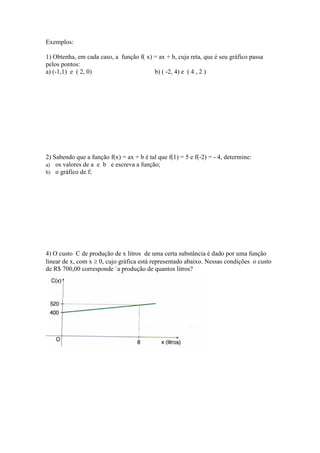
29. 5) Dado a função y = - x² + 2x + 8 determine:
a) o valor máximo
b) a imagem
c) a concavidade
d) a função é crescente entre x = 1 e x = 3
e) o domínio
f) as raízes
g) o valor de y quando x = 5
resposta da questão 5:
a) O valor máximo é obtido com o Yv, para isso precisamos do valor do
∆ = b 2 − 4ac
− ∆ − 36
Então Yv = = = 9 este é o valor máximo.
4a − 4
b) Im = ] − ∞,9] imagem da função do segunda grau é sempre o Yv quando
definida em Reais
c) Como a < 0 então concavidade voltada para baixo
d) Quando x = 1 trem se y = 9 e quando x = 3 tem-se y = 5 então é decrescente
diminuiu o valor.
e) Domínio é todos os reais
f) as raízes são x’ = 4 e x” = -2 pontos onde a parábola corta o eixo x
g) quando x = 5 tem-se y = -(5)² + 2.5 + 8 então y = -25 + 10 + 8 então y = -
7
Visualize todos os cálculos que você realizou no gráfico
y f(x)=- x^2 + 2x + 8
9
8
7
6
5
4
3
2
1
x
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-1
-2
-3
-4
-5
-6
-7
-8
-9

30. Seguimos nossos estudos nas funções agora destacando a função do
primeiro grau.
ESTUDO DA FUNÇÃO POLINOMIAL DO 1º GRAU
É uma função polinomial do primeiro grau quando a sua representação
matemática é um polinômio de grau 1 do tipo y = ax +b
Modelando funções a partir de situações problemas.
1) Na produção de peças, uma indústria tem custo fixo de R$ 5,00 mais um custo
variável de R$ 1,50 por unidade produzida. Sendo x o número de unidades
produzidas. Represente algebricamente o custo em função do número de peças e
graficamente o custo referente a 6 peças
Representações intermediárias
Variáveis unidades Representação adotada no
problema
DEFINIÇÃO:
Uma função f: R em R chama-se função afim ou função do 1º grau quando existem
dois números reais a e b tais que f(x) = ax + b, sendo a e b números reais, para
todo x ∈ R e x é a variável independente.
Ex.: f(x) = 2x – 1 g(x) = x – 4 h(x) = x
Graficamente a função do 1º grau é representada por uma reta.
Ex.: Represente graficamente as funções abaixo:
a) f(x) = x – 3 b) g(x) = - x + 4 c) f(x) = 2.
OBS.: O a é também chamado de coeficiente angular da reta, representa o ângulo
que a reta faz com o eixo das abscissas (x). O b é também chamado de coeficiente
linear, representa o ponto que a reta passa pelo eixo das ordenadas (y).
Determinação de uma função polinomial do primeiro grau a partir do gráfico.
Uma função do primeiro grau f(x) = ax + b fica inteiramente determinada quando
conhecemos dois dos seus pontos.
Ex.:

31. Exemplos:
1) Obtenha, em cada caso, a função f( x) = ax + b, cuja reta, que é seu gráfico passa
pelos pontos:
a) (-1,1) e ( 2, 0) b) ( -2, 4) e ( 4 , 2 )
2) Sabendo que a função f(x) = ax + b é tal que f(1) = 5 e f(-2) = - 4, determine:
a) os valores de a e b e escreva a função;
b) o gráfico de f;
4) O custo C de produção de x litros de uma certa substância é dado por uma função
linear de x, com x ≥ 0, cujo gráfica está representado abaixo. Nessas condições o custo
de R$ 700,00 corresponde `a produção de quantos litros?

32. ZERO OU RAIZ DA FUNÇÃO POLINOMIAL DO 1º GRAU
Situação problema:
Uma indústria implantou em programa de prevenção de acidentes de trabalho. Essa
programa prevê que o número y de acidentes varie em função do tempo t ( em anos) de
acordo com a lei y = 28,8 – 3,6 t. nessas condições, quantos anos levará para essa
indústria erradicar os acidentes de trabalho?
Definição:
Zero ou raiz de uma função é o valor de x para o qual a função f(x) = ax + b se anula,
ou seja, o valor para o qual f(x)= 0. Graficamente o zero ou raiz representa o ponto que
a reta passa pelo eixo x ( abscissas).
Para determinar o zero ou raiz basta resolver a equação ax + b = 0.
Exemplos: determine o zero ou raiz das funções abaixo:
a) f(x) = x + 2 b) f(x) = 3x –1 c) f(x) = -2x + 5
CRESCIMENTO DA FUNÇÃO POLINOMIAL DO 1º GRAU
O que determina se a função f(x) = ax +b, com a ≠ 0, e crescente ou decrescente é o
sinal de a . Assim:
Se a > 0 é uma função crescente
Se a < 0 é uma função decrescente.
Ex.: determine se as funções abaixo são crescentes ou decrescentes.
a) f(x) = x – 4 b) f(x) = -x/3 +1 c) f(x) = 2x d) f(x) = -x +2
Estudo do sinal da função polinomial do 1º grau
Estudar o sinal da função significa determinar os valores de x para os quais a função
f(x) é positiva, negativa ou igual a zero.

33. Situação problema:
Após o pagamento de todos os custos na importação de um produto, uma empresa
calcula o faturamento que terá com o mesmo usando a lei f(x) = 8x – 640, onde f(x) é
o faturamento líquido e x unidades vendidas. Qual a quantidade mínima que essa
empresa terá de vender para obter lucro?
Outros exemplos:
Faça o estudo do sinal das funções abaixo definidas em R.
a) f(x) = 3x + 1 b) f(x) = 2 – 6x c) f(x) = x -5
EXERCÍCIOS
1)Dada a função afim f(x) = 5x - 1, determine:
a) f(1) b) f(0) c) f(1/5)
2)Na produção de peças uma indústria tem um custo fixo de R$ 8,00 mais um custo
variável de R$ 50,00 por unidade produzida . Sendo x o número de unidades
produzidas:
a) escreva a lei da função que fornece o custo total de x peças;
b) calcule o custo de 100 peças.
3)Construa, num sistema cartesiano ortogonal, o gráfico das seguintes funções:
a) f(x) = 2x +3 b) f(x) = -2x +5
4) Sem construir gráficos , descubra os pontos em que as retas, cortam os eixos x e y:
a) f(x) = x – 5 b) f(x) = -2x c) f(x) = 2 – ¾ x d) f(x) = 1 + 4x
5) ( Unificado – RJ) Uma barra de ferro com temperatura inicial de –10 ºC foi aquecida
até 30 ºC. o gráfico abaixo representa a variação da temperatura da barra em função do

34. tempo gasto nessa experiência. Calcule em quanto tempo, após o início da experiência,
a temperatura da barra atingiu 0 ºC.
Finalizando o estudo das funções e suas representações vamos estudar
a função definida por várias sentenças.
FUNÇÃO DEFINIDA POR VÁRIAS SENTENÇAS
As funções definidas por várias sentenças aparecem em diferentes
situações em nosso contexto, por exemplo na conta de energia de nossa casa,
na conta de água, no ingresso do cinema entre outras situações.
ENEM 2010

35. Exemplo:
1) Uma papelaria cobra R$ 0,10 por página xerocada, caso o número de
páginas seja inferior ou igual a 50.se o número de páginas for superior a 50, o
custo por página adicional passa a ser R$ 0,08. escreva a lei que representa o
valor gasto em função do número de páginas xerocadas.
2) Construa o gráfico das funções abaixo definidas em R e determine o
conjunto imagem.
2 x, se ≥ 0
a) f(x) =  2
 x , se x < 0
 x 2 + 1, se > 1
b) f(x) = 
 x − 3, se x ≤ 1
3, se ≥ 2
c) f (x) = 
 x − 1, se x < 2

36. Agora que finalizamos o estudo das funções vamos finalizar nosso
semestre estudando as inequações. Assim como as funções as inequações
podem ser de diferentes tipos. Vamos estudar cada tipo.
O ESTUDO DAS INEQUAÇÕES E SEUS ALGOTIMOS DE
RESOLUÇÃO
As inequações aparecem em diferentes situações em nosso contexto.
Por exemplo:
1)A receita mensal em reais de uma empresa é r = 20 000p – 2000p²
onde p é o preço de venda de cada unidade. Para que valores de p a receita é
inferior a R$ 37 500,00?
2)Determine o conjunto solução das inequações abaixo
a) x ² - 2x >0 b) 3(x+1) – 6 < o

37. x−2
>0
c) 1 − x d) x( x 2 − 4)
≤0
x−3
1
2x > 8 ( )x > 8
e) f) 2
g) log 2 x < 3 h) log 1 x < 3
2
x 2 − 4x + 3 > 0

i)
x(x + 4) > − 4(x + 4) j)  2
x − 2x < 0

l) |2x-3| <5 m) |2-x | > 1