Este documento discute conjuntos e funções matemáticas como uma nova metodologia para ensinar matemática. Apresenta definições e exemplos de conjuntos, operações com conjuntos, intervalos reais, representações de funções e cálculo de valores de funções.

1. A EXPLORAÇÃO DAS INTELIGÊNCIAS MÚLTIPLAS COMO UMA NOVA METODOLOGIA PARA O ENSINO DA MATEMÁTICA CONJUNTOS E FUNÇÕES ICD – INSTITUTO DA CULTURA E DESENVOLVIMENTO CAMPO MOURÃO MARÇO - 2010 PROFESSOR: JOÃO ALESSANDRO EMAIL/MSN: [email_address] GMAIL/GOOGLE TALK: [email_address] TWITTER: www.twitter.com/jalmat ORKUT: http://www.orkut.com.br/Main#Profile?uid=16471219565289082570

2. CONJUNTOS INTRODUÇÃO Um conjunto é considerado um dos conceitos mais básicos da matemática, sendo o elemento principal da teoria de conjuntos . Um conjunto é apenas uma coleção de entidades, chamadas de elementos. A notação padrão lista os elementos separados por vírgulas e delimitados por chaves.

3. CONJUNTOS 1. Conceitos essenciais: Conjunto : representa uma coleção de objetos, sempre representado por letras maiúsculas. Elemento : qualquer um dos componentes de um conjunto, geralmente representado por letras minúsculas. Pertinência : é a característica associada a um elemento que faz parte de um conjunto. 2. Pertence ou não pertence Se a é um elemento de A , nós podemos dizer que o elemento a pertence ao conjunto A e podemos escrever .Se a não é um elemento de A , nós podemos dizer que o elemento a não pertence ao conjunto A e podemos escrever .

4. RESOLVENDO EXERCÍCIOS 1. Escreva os conjuntos a seguir, classificando-os em universo, unitário ou vazio: a) A = { x/x é o conjunto dos números naturais maiores que 2} A = { 3, 4, 5, 6, 7, 8, 9, 10, ...} Conjunto Universo (possui mais de 1 elemento). b) B = { x/x é o mês do ano começado com a letra x} c) C = { x/x é o dia da semana começado com a letra d} C = { domingo } Conjunto Unitário (possui apenas 1 elemento). B = { } ou B = Conjunto Vazio (não possui nenhum elemento).

5. CONJUNTOS 3. OPERAÇÕES COM CONJUNTOS: C) DIFERENÇA: A - B “ SÃO OS ELEMENTOS QUE ESTÃO EM A E NÃO ESTÃO EM B”. UNIÃO: “ BASTA ESTAR EM UM PARA ESTAR NA UNIÃO”. B) INTERSECÇÃO: “ SÓ ESTÁ NA INTERSECÇÃO QUEM ESTÁ EM TODOS OS CONJUNTOS”.

6. RESOLVENDO EXERCÍCIOS 2. Dados os conjuntos A = {0, 2, 3, 5}, B = {1, 2 , 4, 10 } e C = {0, 2, 4 }, determine: { 0, 1, 2, 3, 4, 5, 10} { 0, 1, 2, 4,10 } { 2 } { 2, 4 } { 0, 3, 5 } { 0 }

7. CONJUNTOS 4. INTERVALOS REAIS PARA PENSAR: QUANTOS NÚMEROS REAIS EXISTEM ENTRE 0 E 1? RESPOSTA: EXISTEM INFINITOS NÚMEROS REAIS: EXEMPLIFICANDO: 0,1; 0,12; 0,102; 0,5; 0,9; 0,99; 0,999.

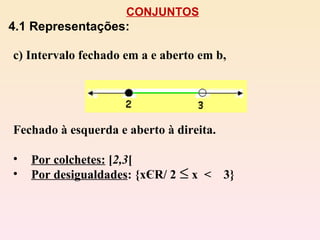
8. CONJUNTOS 4.1 Representações: Intervalo aberto em a e aberto em b, Aberto à esquerda e aberto à direita. Por colchetes: ] 2,3 [ Por desigualdades : {xЄR/ 2 < x < 3}

9. CONJUNTOS 4.1 Representações: b) Intervalo aberto em a e fechado em b, Aberto à esquerda e fechado à direita. Por colchetes: ] 2,3 ] Por desigualdades : {xЄR/ 2 < x 3}

10. CONJUNTOS 4.1 Representações: c) Intervalo fechado em a e aberto em b, Fechado à esquerda e aberto à direita. Por colchetes: [ 2,3 [ Por desigualdades : {xЄR/ 2 x < 3}

11. CONJUNTOS 4.1 Representações: 4.1.1 Intervalos Infinitos: Lembrete: O infinito sempre é intervalo aberto e sem bolinha! a) {x Є R/x > a} Aberto à esquerda e vai para o infinito positivo. Por colchetes: ] 2, [ Por desigualdades : {xЄR/ x > 2}

12. CONJUNTOS 4.1 Representações: 4.1.1 Intervalos Infinitos: b) {x Є R/x < a} Aberto à direita e vai para o infinito negativo. Por colchetes: ] , 2 [ Por desigualdades : {xЄR/ x < 2}

13. CONJUNTOS 4.1 Representações: 4.1.1 Intervalos Infinitos: c) {x Є R/x≥a} Fechado à direita e vai para o infinito positivo. Por colchetes: [ 2, [ Por desigualdades : {xЄR/ x ≥ 2}

14. CONJUNTOS 4.1 Representações: 4.1.1 Intervalos Infinitos: d) {x Є R/≤a} Fechado à direita e vai para o infinito positivo. Por colchetes: ] , 2 ] Por desigualdades : {xЄR/ x ≤ 2}

15. FUNÇÕES

16. FUNÇÃO FUNÇÃO É UM DOS CONCEITOS MAIS ÚTEIS EM MATEMÁTICA E EM TODOS OS RAMOS DA TECNOLOGIA. TAIS COMO A FÍSICA, A MECÂNICA E A ELETRICIDADE. DEFINIÇÃO DADOS DOIS CONJUNTOS NÃO-VAZIOS, FUNÇÃO DE A EM B É QUALQUER RELAÇÃO DE A EM B EM QUE CADA ELEMENTO DE A ASSOCIA UM ÚNICO ELEMENTO DE B. REPRESENTAÇÃO POR TABELAS, DIAGRAMAS E GRÁFICOS.

17. Exemplo: OBSERVE A TABELA QUE RELACIONA O NÚMERO DE LITROS DE COMBUSTÍVEL CONSUMIDO POR UM VEÍCULO COM OS PRIMEIROS 40 Km PERCORRIDOS. REPRESENTAÇÃO POR TABELA:

18. ESSA RELAÇÃO CARACTERIZA UMA FUNÇÃO DEFINIDA PELA EQUAÇÃO y= 8X O SEU DOMÍNIO É REPRESENTADO PELOS VALORES DE X DA TABELA; D ( f ) = {0,1,2,3,4,5} O SEU CONJUNTO-IMAGEM REPRESENTADO PELOS VALORES DE Y, OS QUAIS ESTÃO ASSOCIADOS A CADA X DO DOMÍNIO: Im ( f ) = {0,8,16,24,32,40}

19. REPRESENTAÇÃO POR DIAGRAMAS: 1 2 3 4 5 8 16 24 32 40 A B f : A -> B 0 0 X Y 0 0 1 8 2 16 3 24 4 32 5 40

20. 1 0 2 3 4 5 x 8 16 24 32 40 y REPRESENTAÇÃO GRÁFICA: X Y 0 0 1 8 2 16 3 24 4 32 5 40

21. EXERCÍCIOS RÁPIDOS: ANALISANDO CASOS DE FUNÇÕES 1. Diga quais diagramas abaixo que representam funções: Não é função, pois x = 4 não tem imagem! B 1 2 3 4 8 16 24 A a)

22. É função! Pois cada x tem um único y. D(f) = { 4, 5, 6 } CD(f) = { 6, 7, 8, 9 } Im(f) = { 6, 7, 8 } Observe que y = 9 é contra-domínio, porém não é imagem, pois não recebe relação de x. B 4 5 6 9 6 7 8 A b) f : A -> B

23. Não é função! Pois pela definição de função, cada x deve ter um único valor relacionado a y. E para x = 3, temos dois valores: y = 9 e y =12. Ou seja, x tem 2 valores, portanto, a relação acima não é função. B 1 2 3 12 0 4 9 A c)

24. RECONHECENDO SE UM GRÁFICO É FUNÇÃO: Corta-se o gráfico com 2 retas paralelas ao eixo y. Se as retas cortarem o gráfico em apenas 1 ponto, o gráfico é de uma função. Caso contrário, não é função.

25. EXERCÍCIO Assinale quais gráficos que representam funções: Não é função Não é função É função É função x y x y x y x y ( ) ( ) d( ) c( )

26. CALCULANDO f(x) Lembrete: f(x) = y Exemplo: Sendo f(x) = 3x +1. Determine: a) f(1) = ? f(x) = 3x +1 f(1) = 3 . 1 + 1 f(1) = 3 + 1 f(1) = 4 b) f(-2) = ? f(x) = 3x +1 f(-2) = 3 . (-2) + 1 f(-2) = - 6 + 1 f(-2) = -5

27. RESOLVENDO EXERCÍCIOS 1. Observe o gráfico da função abaixo: Complete as questões seguintes: f (-4) = f (2) = f (3) = A função é crescente nos intervalos: A função é decrescente nos intervalos: A função é constante em: 5 6 3 [1;2] [-4;-2] e [2; 3,5] [-2, 1] y x -4 -2 1 2 3 3 5 6 3,5

28. LEMBRETE ESTA APRESENTAÇÃO ESTÁ NO EMAIL DO CURSO: SITE: www.hotmail.com LOGIN: icd_cursos@hotmail.com SENHA: caixa2010

29. Dúvidas